
全程设计 第三章 函数的慨念与性质 3.4。 函数的应用(一)
第三章 函数的概念与性质 3.4 函数的应用(一)

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航、 课前·基础认知 1.几类常见的函数模型 名称 解析式 条件 一次函数模型 y=kx+b 0 反比例函数模型 y-ktb 0
导航 课前·基础认知 1.几类常见的函数模型 名称 解析式 条件 一次函数模型 y=kx+b k≠0 反比例函数模型 y= 𝐤 𝐱 +b k≠0

导航 名称 解析式 条件 般式:y=x2+bx+c, 二次函数模型 顶点式a++ ac-b2 呋0 4a 幂函数型模型 y=ax"+b 呋0,n≠1 分段函数模型 f(X),x∈11, (gx,x∈2
导航 名称 解析式 条件 二次函数模型 一般式:y=ax2 +bx+c, 顶点式:y=a(x+ 𝐛 𝟐𝐚 ) 2 + 𝟒𝐚𝐜-𝐛 𝟐 𝟒𝐚 a≠0 幂函数型模型 y=axn +b a≠0,n≠1 分段函数模型 y= 𝐟(𝐱),𝐱∈𝐈 𝟏, 𝐠(𝐱),𝐱∈𝐈 𝟐 —

导航 2.解函数应用题的一般步骤 第一步:阅读理解、认真审题 第二步:引进数学符号,建立数学模型.根据问题的已知条件, 运用已掌握的数学知识、物理知识及其他相关知识建立函数 关系式,将实际问题转化为数学问题,实现问题的数学化,即所 谓建立数学模型
导航 2.解函数应用题的一般步骤 第一步:阅读理解、认真审题. 第二步:引进数学符号,建立数学模型.根据问题的已知条件, 运用已掌握的数学知识、物理知识及其他相关知识建立函数 关系式,将实际问题转化为数学问题,实现问题的数学化,即所 谓建立数学模型

导 第三步:利用数学方法解答得到的常规数学问题(即数学模型), 求得结果 第四步:转译成具体问题作出解答 注意:()要特别关注实际问题的自变量的取值范围,合理确定 函数的定义域;(2)在解决函数模型后,必须验证解的合理性
导航 第三步:利用数学方法解答得到的常规数学问题(即数学模型), 求得结果. 第四步:转译成具体问题作出解答. 注意:(1)要特别关注实际问题的自变量的取值范围,合理确定 函数的定义域;(2)在解决函数模型后,必须验证解的合理性
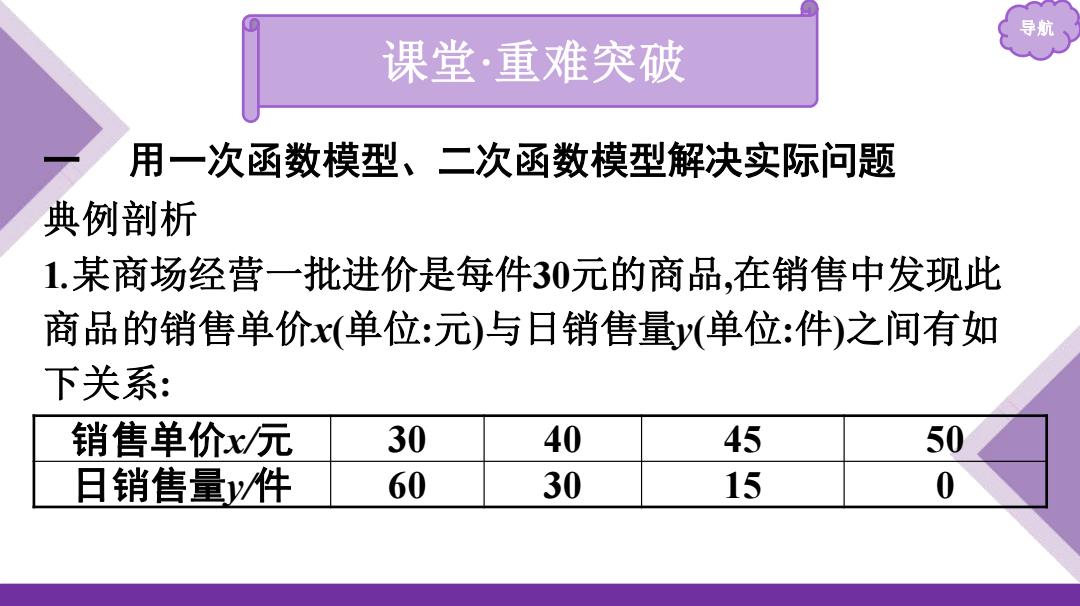
导航 课堂·重难突破 用一次函数模型、二次函数模型解决实际问题 典例剖析 1.某商场经营一批进价是每件30元的商品,在销售中发现此 商品的销售单价x(单位:元)与日销售量y(单位:件)之间有如 下关系: 销售单价x/元 30 40 45 50 日销售量/件 60 30 15 0
导航 课堂·重难突破 一 用一次函数模型、二次函数模型解决实际问题 典例剖析 1.某商场经营一批进价是每件30元的商品,在销售中发现此 商品的销售单价x(单位:元)与日销售量y(单位:件)之间有如 下关系: 销售单价x/元 30 40 45 50 日销售量y/件 60 30 15 0

导航 ()在平面直角坐标系中,根据表中提供的数据描出实数对心y) 对应的点,并确定x与y的一个函数解析式y=x); (2)设经营此商品的日销售利润为P(单位:元),根据上述解析式 写出P关于x的函数解析式,并指出销售单价x为多少时,才能 获得最大日销售利润
导航 (1)在平面直角坐标系中,根据表中提供的数据描出实数对(x,y) 对应的点,并确定x与y的一个函数解析式y=f(x); (2)设经营此商品的日销售利润为P(单位:元),根据上述解析式 写出P关于x的函数解析式,并指出销售单价x为多少时,才能 获得最大日销售利润

导航 解:()在平面直角坐标系中画出各点,如图 这些点近似地分布在一条直线 /件 60 上,猜想y与x之间的关系为一次 50 函数关系, 40 设Jy=fx)=kc+b(0,且k,b为常数), 30 20 则1g0=80+众解径价=30 10 0 102030405060 x/元 .∴y=fx)=-3x+150,经检验,点(45,15)、点(50,0)也在此直线上 .'y与x之间的函数解析式为y=-3x+150(30≤x≤50)以
导航 解:(1)在平面直角坐标系中画出各点,如图. 这些点近似地分布在一条直线 上,猜想y与x之间的关系为一次 函数关系, 设 y=f(x)=kx+b(k≠0,且 k,b 为常数), 则 𝟔𝟎 = 𝟑𝟎𝒌 + 𝒃, 𝟑𝟎 = 𝟒𝟎𝒌 + 𝒃, 解得 𝒌 = -𝟑, 𝒃 = 𝟏𝟓𝟎. ∴y=f(x)=-3x+150,经检验,点(45,15)、点(50,0)也在此直线上. ∴y与x之间的函数解析式为y=-3x+150(30≤x≤50)

导航、 (2)由题意,得P=(c-30)(-3x+150)=-3x2+240x-4500 =-3x-40)2+300(30≤x≤50), ∴.当x=40时,P有最大值300. 故当销售单价为40元时,日销售利润最大
导航 (2)由题意,得P=(x-30)(-3x+150)=-3x 2+240x-4 500 =-3(x-40)2+300(30≤x≤50). ∴当x=40时,P有最大值300. 故当销售单价为40元时,日销售利润最大