
全程设计 第一章 集合与常用逻辑用语 1.3 集合的基本运算 第1课时 并集、交集
第一章 集合与常用逻辑用语 1.3 集合的基本运算 第1课时 并集、交集

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破
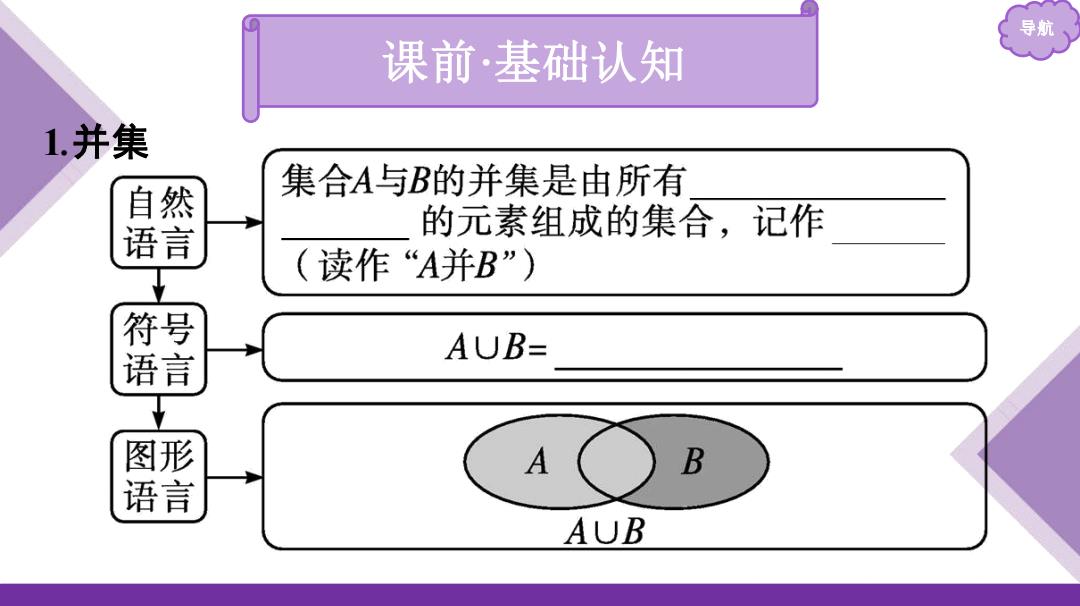
导航 课前·基础认知 1.并集 自然 集合A与B的并集是由所有 语言 的元素组成的集合,记作 读作“A并B”) ( 符号 语言 AUB- 图形 A B 语言 AUB
导航 课前 ·基础认知 1 . 并 集

导航 微思考(1)“x∈A或x∈B”包含哪几种情况? (2)集合AUB的元素个数是否等于集合A与集合B的元素个数 之和?
导航 微思考 (1)“x∈A或x∈B”包含哪几种情况? (2)集合A∪B的元素个数是否等于集合A与集合B的元素个数 之和?

导航 提示:(1)“x∈A或x∈B”这一条件包括下列三种情况:x∈A,但 xB;x∈B,但x庄Ax∈A,且x∈B.用Venn图表示如图所示. A B A B x∈A,但x年Bx∈B,但xA A B x∈A,且x∈B (2)不一定等于,AUB的元素个数小于或等于集合A与集合B 的元素个数之和
导航 提示:(1)“x∈A或x∈B”这一条件包括下列三种情况:x∈A,但 x∉B;x∈B,但x∉A;x∈A,且x∈B.用Venn图表示如图所示. (2)不一定等于,A∪B的元素个数小于或等于集合A与集合B 的元素个数之和
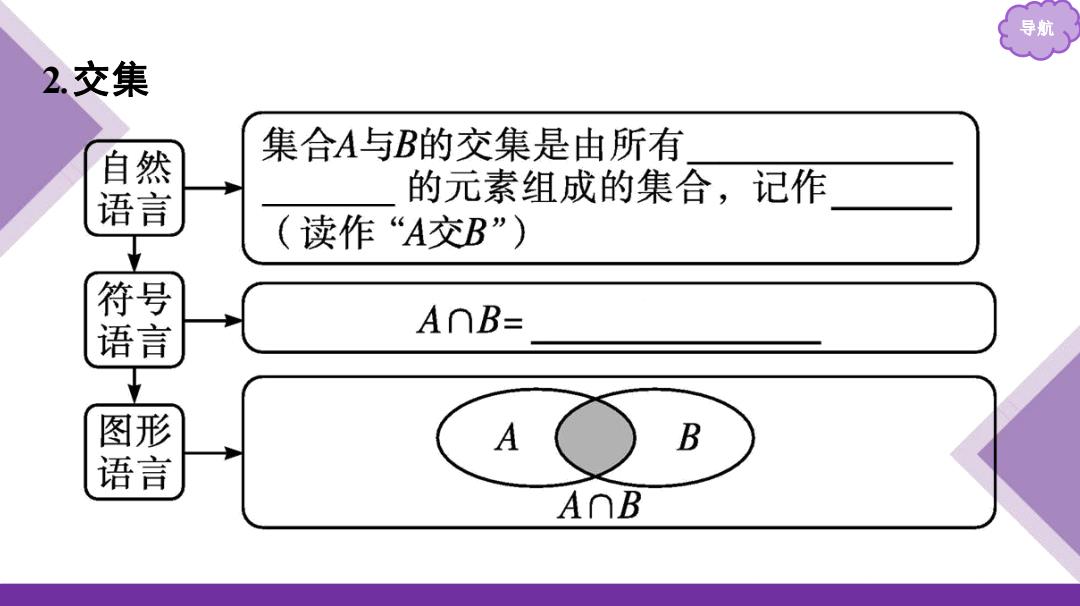
导航 2.交集 集合A与B的交集是由所有 餐 的元素组成的集合,记作 (读作“A交B”) 雷 A∩B= 图形 A B 语言 A∩B
导航 2 .交集

导航 3.并集与交集的运算性质 并集的运算性质 交集的运算性质 AUB-BUA A∩B=B∩A AUA= A∩A= AU⑦= A∩②=
导航 3.并集与交集的运算性质 并集的运算性质 交集的运算性质 A∪B=B∪A A∩B=B∩A A∪A= A A∩A= A A∪⌀= A A∩⌀= ⌀

导航 课堂·重难突破 并集的概念及其应用 典例剖析 1.(1)设集合M={x2+2=0},N={xx2-2=0},则MUN=( A.{0} B.{0,2 C.{-2,0} D.{-2,0,2} (2)已知集合M={x-35},则MUN=( A.{xx3} B.{x-55}
导航 课堂·重难突破 一 并集的概念及其应用 典例剖析 1.(1)设集合M={x|x2+2x=0},N={x|x2 -2x=0},则M∪N=( ) A.{0} B.{0,2} C.{-2,0} D.{-2,0,2} (2)已知集合M={x|-35},则M∪N=( ) A.{x|x-3} B.{x|-55}

导航 答案:1)D(2)A 解析:(1)M={xx2+2x=0}={0,-2},N={xx2-2x=0}={0,2},则 MUN={-2,0,2. 故选D. (2)在数轴上表示集合M,N,如图所示,由图可知,MUN={3}. N -5-3 0
导航 答案:(1)D (2)A 解析:(1)M={x|x2+2x=0}={0,-2},N={x|x2 -2x=0}={0,2},则 M∪N={-2,0,2}. 故选D. (2)在数轴上表示集合M,N,如图所示,由图可知,M∪N={x|x-3}

导航 规律总结 求集合并集的两种方法 ()定义法:若是用列举法表示的数集,可以根据并集的定义直 接观察或用Venn图表示出集合运算的结果, (2)数形结合法:若是用描述法表示的数集,可借助数轴分析写 出结果,此时要注意当端点不在集合中时,应用“空心圈”表示
导航 求集合并集的两种方法 (1)定义法:若是用列举法表示的数集,可以根据并集的定义直 接观察或用Venn图表示出集合运算的结果. (2)数形结合法:若是用描述法表示的数集,可借助数轴分析写 出结果,此时要注意当端点不在集合中时,应用“空心圈”表示