
全程设计 第一章 集合与常用逻辑用语 1.2 集合间的基本关系
第一章 集合与常用逻辑用语 1.2 集合间的基本关系

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 L.Venn图的优点及其表示 (1)优点:形象直观 (2)表示:经常用平面上 曲线的 代表集合
导航 课前·基础认知 1.Venn图的优点及其表示 (1)优点:形象直观. (2)表示:经常用平面上 封闭 曲线的 内部 代表集合
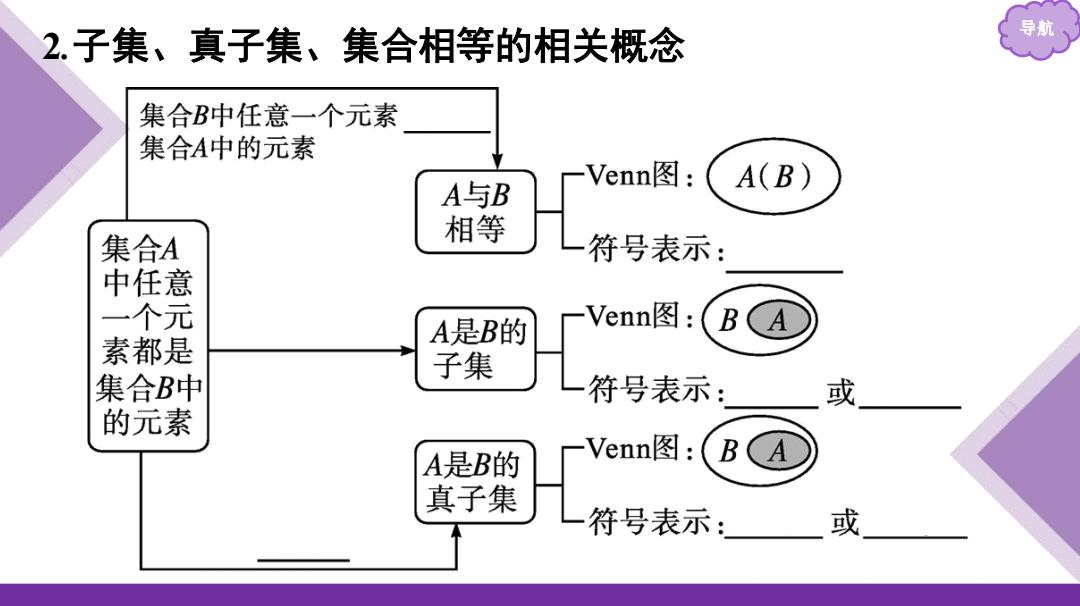
2.子集、真子集、集合相等的相关概念 导航 集合B中任意一个元素 集合A中的元素 -Venn图: A与B A(B) 集合A 相等 符号表示: 中任意 一个元 A是B的 Venn图:(BA 素都是 子集 集合B中 符号表示: 或 的元素 A是B的 -Venn图:(B A 真子集 符号表示: 或
导航 2 .子集、真子集、集合相等的相关概念

导期 微思考1(1)任何两个集合之间是不是都有包含关系? 2)符号“∈”与“二”有何不同? 提示:(1)不一定.如集合A={0,1,2},B={-1,0,1},这两个集合就没 有包含关系. (2)符号“∈”表示元素与集合间的关系; 而“二”表示集合与集合间的关系
导航 微思考1 (1)任何两个集合之间是不是都有包含关系? (2)符号“∈”与“⊆”有何不同? 提示:(1)不一定.如集合A={0,1,2},B={-1,0,1},这两个集合就没 有包含关系. (2)符号“∈”表示元素与集合间的关系; 而“⊆”表示集合与集合间的关系

导航 3.空集 ()定义:不含 元素的集合叫做空集,记为 (2)规定: 是任何集合的子集 微思考2{0}与o相同吗? 提示:不同.{0}表示一个集合,且集合中有且仅有一个元素0;而 ⑦表示空集,其不含有任何元素,故{0}与⑦不相同
导航 3.空集 (1)定义:不含 任何 元素的集合叫做空集,记为 ⌀ . (2)规定: 空集 是任何集合的子集. 微思考2 {0}与⌀相同吗? 提示:不同.{0}表示一个集合,且集合中有且仅有一个元素0;而 ⌀表示空集,其不含有任何元素,故{0}与⌀不相同

导航、 4集合间关系的性质 (1)任何一个集合是它本身的子集,即A二A. (2)对于集合A,B,C, ①若A二B,且BCC,则A二C; ②若AB,BC,则AC. (3)若A二B,A≠B,则AB
导航 4.集合间关系的性质 (1)任何一个集合是它本身的子集,即A⊆A. (2)对于集合A,B,C, ①若A⊆B,且B⊆C,则A⊆C; ②若A⫋B,B⫋C,则A⫋C. (3)若A⊆B,A≠B,则A⫋B

导航 课堂·重难突破 集合间关系的判断 典例剖析 1.(1)已知集合M={xx2-x=0},N={0,1,2,则M与N间的关系表示 正确的是( A.MEN B.M∈N C.MSN D.NCM (2)已知集合A={x-1x<4,B={xx<5},则() A.A∈B B.ASB C.BSA D.BCA
导航 课堂·重难突破 一 集合间关系的判断 典例剖析 1.(1)已知集合M={x|x2 -x=0},N={0,1,2},则M与N间的关系表示 正确的是( ) A.M=N B.M∈N C.M⫋N D.N⊆M (2)已知集合A={x|-1<x<4},B={x|x<5},则( ) A.A∈B B.A⫋B C.B⫋A D.B⊆A

导航 答案:1)C(2)B 解析:1)解方程x2x=0,得x=0或x=1,则M={1,0} 1∈M,且1∈N,0∈M,且0∈W, .∴.McN. 又2∈N,且2EM,.'.MN. 故选C (2)用数轴表示集合A,B,如图所示. A B 由图可知,A军B.-21012 3
导航 答案:(1)C (2)B 解析:(1)解方程x 2 -x=0,得x=0或x=1,则M={1,0}. ∵1∈M,且1∈N,0∈M,且0∈N, ∴M⊆N. 又2∈N,且2∉M,∴M⫋N. 故选C. (2)用数轴表示集合A,B,如图所示. 由图可知,A⫋B

导航 规律总结 判断集合间关系的方法 ()观察法:将元素一一列举观察. (2)元素特征法:首先确定集合的元素是什么,弄清集合元素的 特征,再利用集合元素的特征判断关系 (3)数形结合法:利用数轴或Venn图. 提醒:若ACB和AB同时成立,则AB更能准确表达集合A,B 之间的关系
导航 判断集合间关系的方法 (1)观察法:将元素一一列举观察. (2)元素特征法:首先确定集合的元素是什么,弄清集合元素的 特征,再利用集合元素的特征判断关系. (3)数形结合法:利用数轴或Venn图. 提醒:若A⊆B和A⫋B同时成立,则A⫋B更能准确表达集合A,B 之间的关系