
全程设计 第三章 函数的概念与性质 3.2 丞数的基本性质 3.2.1 单调性与最大(小)值
第三章 函数的概念与性质 3.2 函数的基本性质 3.2.1 单调性与最大(小)值

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导 课前·基础认知 1,增函数与减函数的定义 条 一般地,设函数fx)的定义域为D,区间ICD:如果x1x2∈I,当 件 ≤北2时 都有 都有 那么就称函数fx)在区间I上 那么就称函数fx)在区间I上单 结单调递 ,特别地,当函数调递 ,特别地,当函数fx) 论x)在它的定义域上单调递增 在它的定义域上单调递减时,我 时,我们就称它是 ·函数 们就称它是 函数
导航 课前·基础认知 1.增函数与减函数的定义 条 件 一般地,设函数f(x)的定义域为D,区间I⊆D:如果∀x1 ,x2∈I,当 x1f(x2 ) 结 论 那么就称函数f(x)在区间I上 单调递 增 ,特别地,当函数 f(x)在它的定义域上单调递增 时,我们就称它是 增 函数 那么就称函数f(x)在区间I上单 调递 减 ,特别地,当函数f(x) 在它的定义域上单调递减时,我 们就称它是 减 函数
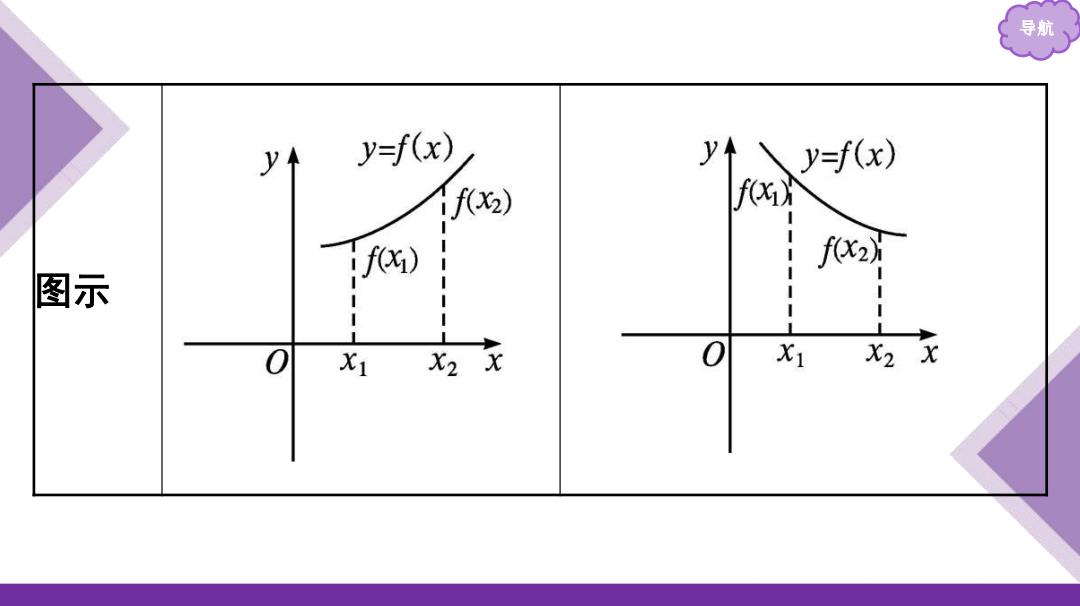
导航 y=f(x) y↑y=f(x) 1f) f》 ifx) 1 f(x2) 图示 0 X1 2大 0 X1 2无
导航 图示

导航 微思考1增(减)函数定义中的xx2有什么特征? 提示:定义中的x1x2有以下3个特征: (1)任意性,即“任意取定义域中的x1水2”中“任意”二字绝不能 去掉,证明时不能以特殊代替一般; (2)有大小,通常规定x1<x2 3)属于同一个单调区间
导航 微思考1 增(减)函数定义中的x1 ,x2有什么特征? 提示:定义中的x1 ,x2有以下3个特征: (1)任意性,即“任意取定义域中的x1 ,x2 ”中“任意”二字绝不能 去掉,证明时不能以特殊代替一般; (2)有大小,通常规定x1<x2 ; (3)属于同一个单调区间
导航 2.函数的单调性与单调区间 如果函数y=fx)在区间I上 或 那么就说函数y=fx)在这一区间具有(严格的)单调性,区间叫 做y=fx)的 区间
导航 2.函数的单调性与单调区间 如果函数y=f(x)在区间I上 单调递增 或 单调递减 , 那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间I叫 做y=f(x)的 单调 区间

导航 微思考2函数y-1在定义域上是减函数吗? 提示:不是,y1在区间(0,0)内单调递减,在区间(0,+0)内也单 调递减,但不能说y1在区间(o,0)U(0,+∞)内单调递减
导航 微思考 2 函数 y= 𝟏 𝒙 在定义域上是减函数吗? 提示:不是.y= 𝟏 𝒙 在区间(-∞,0)内单调递减,在区间(0,+∞)内也单 调递减,但不能说 y= 𝟏 𝒙 在区间(-∞,0)∪(0,+∞)内单调递减

导航 3.函数的最大值与最小值 最值 最大值 最小值 一于 般地,设函数y=fx)的定义域为D,如果存在实数M 条件 满足:x∈D,都有 fx) M fx) M 日xo∈D,使得 结论 M是函数y=fx)的最大值 M是函数y=fx)的最 小值 x)图象上最低点的 几何意义x)图象上最高点的
导航 3.函数的最大值与最小值 最值 最大值 最小值 条件 一般地,设函数y=f(x)的定义域为D,如果存在实数M 满足:∀x∈D,都有 f(x) ≤ M f(x) ≥ M ∃x0∈D,使得 f(x0 )=M 结论 M是函数y=f(x)的最大值 M是函数y=f(x)的最 小值 几何意义 f(x)图象上最高点的纵坐标 f(x)图象上最低点的 纵坐标

导航 微思考3若函数fx)≤M,则M一定是函数的最大值吗? 提示:不一定,只有定义域内存在一点x,使fxo)=M时,M才是 函数的最大值,否则不是
导航 微思考3 若函数f(x)≤M,则M一定是函数的最大值吗? 提示:不一定,只有定义域内存在一点x0 ,使f(x0 )=M时,M才是 函数的最大值,否则不是

导航 课堂·重难突破 函数单调性的判定与证明 典例剖析 1.证明:函数fx)=-x3+1在其定义域上为减函数
导航 课堂·重难突破 一 函数单调性的判定与证明 典例剖析 1.证明:函数f(x)=-x 3+1在其定义域上为减函数