
全程设计 第五章 三角函数 5.4 三角函数的图象与性质 5.4.2 正弦函数、余弦函数的性质 第2课时 正弦函数、余弦函数的单调性与最值
第五章 三角函数 5.4 三角函数的图象与性质 5.4.2 正弦函数、余弦函数的性质 第2课时 正弦函数、余弦函数的单调性与最值

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破
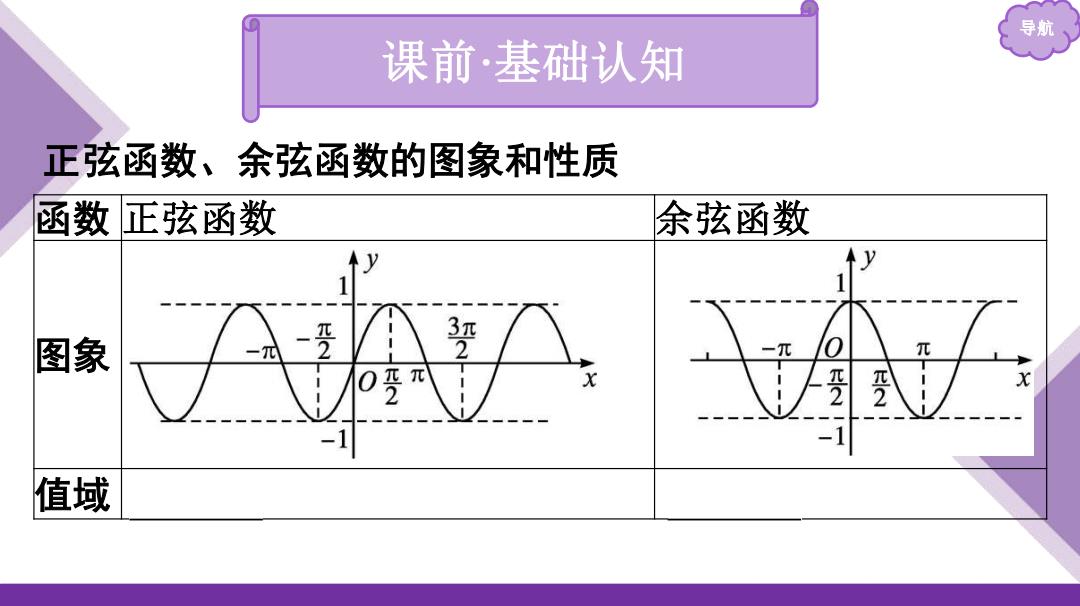
导航 课前·基础认知 正弦函数、余弦函数的图象和性质 函数正弦函数 余弦函数 1 图象 0 元 0受忒 2 -1 值域
导航 课前·基础认知 正弦函数、余弦函数的图象和性质 函数 正弦函数 余弦函数 图象 值域 [-1,1] [-1,1]

导航 函数 正弦函数 余弦函数 正弦函数在每一个闭区间 余弦函数在每一个闭区 上 间 单调 上都单调递增,在每一 都单调递增,在每一个闭区 性 个闭区间 间 上 上 都单调递减 都单调递减
导航 函数 正弦函数 余弦函数 单调 性 正弦函数在每一个闭区间 [- 𝛑 𝟐 +2kπ, 𝛑 𝟐 +2kπ](k∈Z) 上 都单调递增,在每一个闭区 间[ 𝛑 𝟐 +2kπ, 𝟑𝛑 𝟐 +2kπ](k∈Z)上 都单调递减 余弦函数在每一个闭区 间 [-π+2kπ,2kπ](k∈Z) 上都单调递增,在每一 个闭区间 [2kπ,π+2kπ](k∈Z) 上 都单调递减

导航、 函数 正弦函数 余弦函数 当且仅当x= 当且仅当x= 时,ymax=1;当且仅当 最值 时ymax=1;当且仅当x= X- 时ymin=-l 时ymin=-l
导航 函数 正弦函数 余弦函数 最值 当且仅当 x= 𝛑 𝟐 +2kπ(k∈Z) 时,ymax=1;当且仅当 x= - 𝛑 𝟐 +2kπ(k∈Z) 时,ymin=-1 当且仅当 x=2kπ(k∈Z) 时,ymax=1;当且仅当 x= π+2kπ(k∈Z) 时,ymin=-1

导航 微判断(1)正弦函数在定义域上是单调函数.(X) (2)存在实数x,使得cosx=V2.(×) (3)余弦函数y=c0sx在区间[0,π上单调递减.(√) 解析:()正弦函数不是定义域上的单调函数 (2)余弦函数的最大值为1. (3)由余弦函数的单调性可知正确
导航 微判断 (1)正弦函数在定义域上是单调函数.( ) (2)存在实数x,使得cos x= .( ) (3)余弦函数y=cos x在区间[0,π]上单调递减.( ) 解析:(1)正弦函数不是定义域上的单调函数. (2)余弦函数的最大值为1. (3)由余弦函数的单调性可知正确. 𝟐 × ×

导航 微训练函数y=-cosx+3的单调递减区间 为 答案:2kπ-元,2km,k∈Z 解析:y=c0sx的单调递增区间为[2km-元,2k,k∈Z, 'Jy=-c0sx的单调递减区间为[2km-π,2km,k∈Z ∴.函数y=-c0sx+3的单调递减区间为[2km-元,2km,k∈Z
导航 微训练 函数y=-cos x+3的单调递减区间 为 . 答案:[2kπ-π,2kπ],k∈Z 解析:∵y=cos x的单调递增区间为[2kπ-π,2kπ],k∈Z, ∴y=-cos x的单调递减区间为[2kπ-π,2kπ],k∈Z. ∴函数y=-cos x+3的单调递减区间为[2kπ-π,2kπ],k∈Z

导航 课堂·重难突破 求正弦函数、余弦函数的单调区间 典例剖析 1.求函数-sim(-2x+)的单调递减区间
导航 课堂·重难突破 一 求正弦函数、余弦函数的单调区间 典例剖析 1.求函数 y=sin -𝟐𝒙 + 𝛑 𝟔 的单调递减区间

解ysim(-2x+}-(2x君):求函教i(2x+)的 单调递减区间即求ysi(2x爱的单调递增区间. 由2kn2≤2x≤2km+2k∈Z,解得kmx≤km+k∈Z ∴函数-sin(-2x+君)的单调递减区间为m需km+1,k∈Z
导航 解:∵y=sin -𝟐𝒙 + 𝛑 𝟔 =-sin 𝟐𝒙- 𝛑 𝟔 ,∴求函数 y=sin -𝟐𝒙 + 𝛑 𝟔 的 单调递减区间即求 y=sin(2x- 𝛑 𝟔 )的单调递增区间. 由 2kπ- 𝛑 𝟐 ≤2x- 𝛑 𝟔 ≤2kπ+ 𝛑 𝟐 ,k∈Z,解得 kπ- 𝛑 𝟔 ≤x≤kπ+ 𝛑 𝟑 ,k∈Z. ∴函数 y=sin -𝟐𝒙 + 𝛑 𝟔 的单调递减区间为[kπ- 𝛑 𝟔 ,kπ+ 𝛑 𝟑 ],k∈Z

导航 规律总结 用整体替换法求函数y=Asin(0x+p)或y=Acos(wx+p)A,w,p是 常数,A0,0≠0)的单调区间时,若式子中x的系数为负数,则先 利用诱导公式将x的系数变为正数,再求其单调区间.求单调区 间时,需将最终结果写成区间形式
导航 用整体替换法求函数y=Asin(ωx+φ)或y=Acos(ωx+φ)(A,ω,φ是 常数,A≠0,ω≠0)的单调区间时,若式子中x的系数为负数,则先 利用诱导公式将x的系数变为正数,再求其单调区间.求单调区 间时,需将最终结果写成区间形式