
全程设计 第四章 指数数与对数数 4.2指数函数 第1课时 指数函数的概念与图象
第四章 指数函数与对数函数 4.2 指数函数 第1课时 指数函数的概念与图象

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 1.指数函数的概念 一般地,函数y=r(a 0,且M1)叫做指数函数,其中指 数x是自变量,定义域是R
导航 课前·基础认知 1.指数函数的概念 一般地,函数y=ax (a > 0,且a ≠ 1)叫做指数函数,其中指 数x是自变量,定义域是R
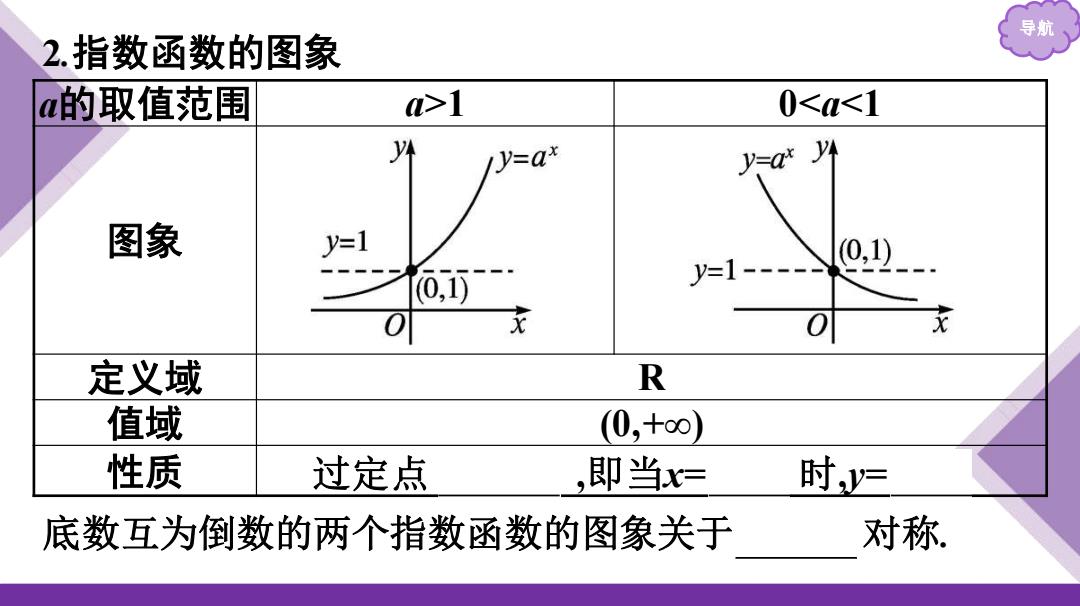
导航 2.指数函数的图象 a的取值范围 >1 0<a<1 y=ar外 图象 y=1 O,D y=1---- 0,1)- 0 x 0 定义域 R 值域 (0,+0) 性质 过定点 ,即当x= 时y= 底数互为倒数的两个指数函数的图象关于 对称
导航 2.指数函数的图象 a的取值范围 a>1 0<a<1 图象 定义域 R 值域 (0,+∞) 性质 过定点 (0,1) ,即当x= 0 时,y= 1 底数互为倒数的两个指数函数的图象关于 y轴 对称
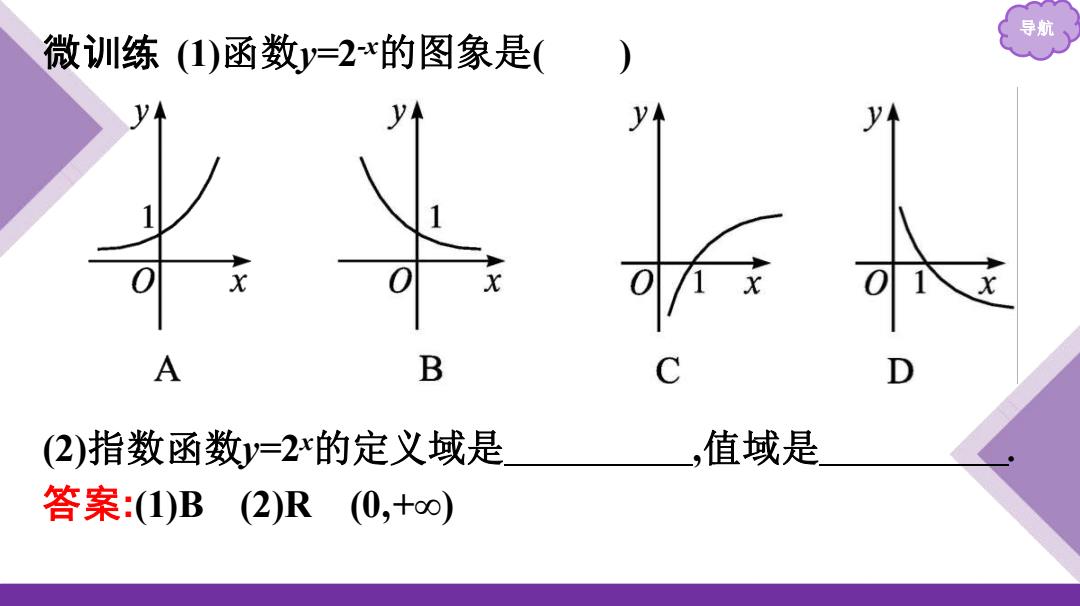
导航 微训练(1)函数y=2x的图象是( A B (2)指数函数y=2x的定义域是 ,值域是 答案:(1)B(2)R(0,+o)
导航 微训练 (1)函数y=2 -x的图象是( ) (2)指数函数y=2 x的定义域是 ,值域是 . 答案:(1)B (2)R (0,+∞)

导航 课堂·重难突破 指数函数的概念 典例剖析 1.(1)给出下列函数:①y=4;②y=x4,③y=-4;④y=(-4;⑤y=π; ⑥y=42;⑦y=x,⑧球2揖揿函数有 填序号) 2已知函数是指数函数,且人》=号,则 3)=
导航 课堂·重难突破 一 指数函数的概念 典例剖析 1.(1)给出下列函数:①y=4 x ;②y=x4 ;③y=-4 x ;④y=(-4)x ;⑤y=π x ; ,其中为指数函数的有 (填序号). (2)已知函数f(x)是指数函数,且 ,则 f(3)= . ⑥y=𝟒 𝒙 𝟐 ;⑦y=xx ;⑧y=(2a-1)x (a> 𝟏 𝟐 ,a≠1) f - 𝟑 𝟐 = 𝟓 𝟐𝟓

答案:1)①⑤⑧ (2)125 解析:(1)由指数函数定义的特征知,②y=x4不符合自变量出现 在指数上,③y=4r不符合心的系数必须为1,④y=(4)'不符合 >0,且1,⑥y=42不符合指数部分只是自变量x,⑦y=x不符 合底数为常数,则填①⑤⑧. 3 2)设e=a*(a>0,且味1,由)= 5z,得=5, 故fx)=5,所以f3)=53=125
导航 答案:(1)①⑤⑧ (2)125 解析:(1)由指数函数定义的特征知,②y=x4不符合自变量出现 在指数上,③y=-4 x不符合a x的系数必须为1,④y=(-4)x不符合 a>0,且a≠1,⑥y= 不符合指数部分只是自变量x,⑦y=xx不符 合底数为常数,则填①⑤⑧. (2)设 f(x)=ax (a>0,且 a≠1),由 f - 𝟑 𝟐 = 𝒂 - 𝟑 𝟐 = 𝟓 𝟐𝟓 = 𝟓 - 𝟑 𝟐,得 a=5, 故 f(x)=5 x ,所以 f(3)=5 3 =125. 𝟒 𝒙 𝟐

导航 3)已知指数函数fx)的图象过点3,π),求函数fx)的解析式. 解:设fx)=(>0,且呋1),将点(3,π)的坐标代入,得f3)=π, 即=π,解得=V元,故fx)=(V元
导航 (3)已知指数函数f(x)的图象过点(3,π),求函数f(x)的解析式. 解:设f(x)=ax (a>0,且a≠1),将点(3,π)的坐标代入,得f(3)=π, 即 a 3 =π,解得 a= 𝝅 𝟑 ,故 f(x)=( 𝛑 𝟑 ) x

导航 规律总结 判断一个函数是不是指数函数的方法 ()看形式,判断一个函数是否为指数函数,关键是看解析式是 否符合y=(>0,且呋1)这一结构形式. (2)明特征,指数函数y=具有以下特征: ①底数a为大于0且不等于1的常数; ②指数位置是自变量x,且x的系数是1; ③r的系数是1
导航 判断一个函数是不是指数函数的方法 (1)看形式,判断一个函数是否为指数函数,关键是看解析式是 否符合y=ax (a>0,且a≠1)这一结构形式. (2)明特征,指数函数y=ax具有以下特征: ①底数a为大于0且不等于1的常数; ②指数位置是自变量x,且x的系数是1; ③a x的系数是1

导航 指数函数图象的应用 典例剖析 2.(1)函数fx)=2心+13(a>0,且呋1)的图象恒过的定点 是 答案:(1)(-1,-1) 解析:因为y=心的图象过定点(0,1), 所以令x+1=0,即x=-1,则-1)=-1, 故fx)=2m+13的图象过定点(-1,-1)
导航 二 指数函数图象的应用 典例剖析 2.(1)函数f(x)=2a x+1 -3(a>0,且a≠1)的图象恒过的定点 是 . 答案:(1)(-1,-1) 解析:因为y=ax的图象过定点(0,1), 所以令x+1=0,即x=-1,则f(-1)=-1, 故f(x)=2a x+1 -3的图象过定点(-1,-1)