
全程设计 第五章 三角数 5.2 三角函数的概念 5.2.1 三角函数的概念 第1课时 三角函数的定义
第五章 三角函数 5.2 三角函数的概念 5.2.1 三角函数的概念 第1课时 三角函数的定义

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破
导航 课前·基础认知 1.利用单位圆定义任意角的三角函数 在直角坐标系中,设a是一个任意角,a∈R,它的终边OP与 相交于点Pcy), P化,yy (1)把点P的纵坐标叫做a的 A(1,0) 记作 ,即y=sina; (2)把点P的横坐标x叫做a的 记作 ,即x=Cosa;
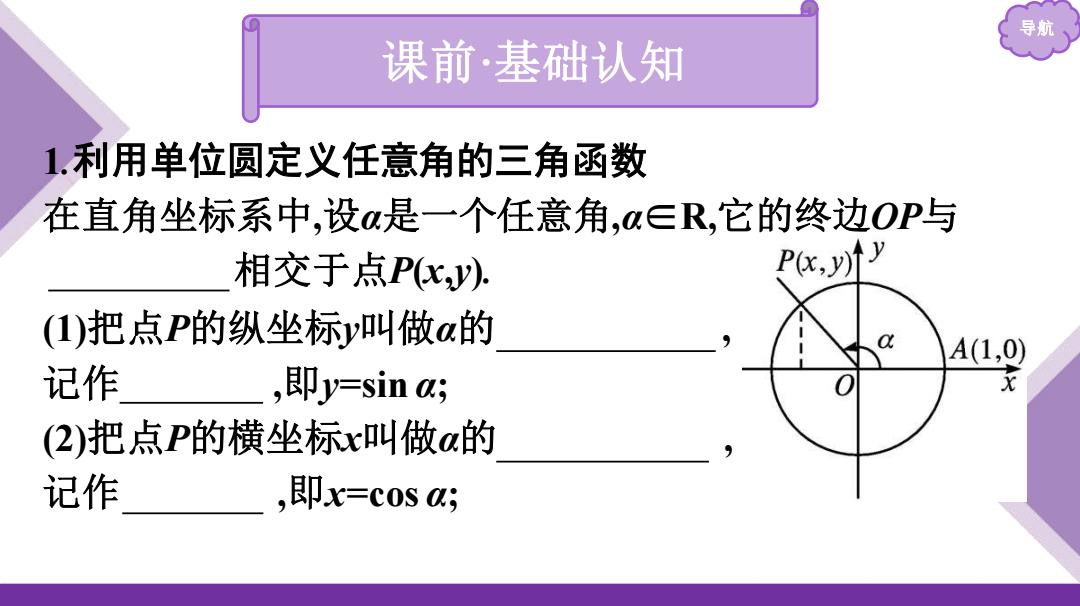
导航 课前·基础认知 1.利用单位圆定义任意角的三角函数 在直角坐标系中,设α是一个任意角,α∈R,它的终边OP与 单位圆 相交于点P(x,y). (1)把点P的纵坐标y叫做α的 正弦函数 , 记作 sin α ,即y=sin α; (2)把点P的横坐标x叫做α的 余弦函数 , 记作 cos α ,即x=cos α;

导航 3)把点P的纵坐标与横坐标的比值兰叫做α的 ,记作 ,即=tana≠0).当≠0时,它也是以角为自变量,以 单位圆上的点的纵坐标与横坐标的比值为函数值的函数,称 为 我们将正弦函数、余弦函数和正切函数统称为
导航 (3)把点P的纵坐标与横坐标的比值 叫做α的 正切 ,记作 tan α ,即 =tan α(x≠0).当x≠0时,它也是以角为自变量,以 单位圆上的点的纵坐标与横坐标的比值为函数值的函数,称 为 正切函数 . 我们将正弦函数、余弦函数和正切函数统称为 三角函数 . 𝒚 𝒙 𝒚 𝒙

导 微总结(1)在任意角的三角函数的定义中,应该明确:x是一个 任意角,其范围是使函数有意义的实数集 (2)要明确sinx是一个整体,不是sin与x的乘积,它是正弦函数 的记号.离开自变量x的“sin“c0s“tan”都是没有意义的. (3)三角函数值是比值,是一个实数,这个实数的大小和点P化y) 在终边上的位置无关,与角的终边位置有关,对于确定的角, 其终边的位置也随之确定
导航 微总结(1)在任意角的三角函数的定义中,应该明确:x是一个 任意角,其范围是使函数有意义的实数集. (2)要明确sin x是一个整体,不是sin与x的乘积,它是正弦函数 的记号.离开自变量x的“sin”“cos”“tan”都是没有意义的. (3)三角函数值是比值,是一个实数,这个实数的大小和点P(x,y) 在终边上的位置无关,与角α的终边位置有关,对于确定的角α, 其终边的位置也随之确定

航 微判断(1)若角a的终边与单位圆交于点(受,受,则sina的 值为竖(V) (2)终边在x轴上的角的正切值不存在.(×) 解析:1)因为根据三角函数在单位圆中的定义,可知 s豆,所以()中说法正流 (2)终边在x轴上的角的正切值为0,故正切值存在.所以(2)中说 法错误
导航 微判断(1)若角 α 的终边与单位圆交于点( 𝟐 𝟐 ,- 𝟐 𝟐 ),则 sin α 的 值为- 𝟐 𝟐 .( ) (2)终边在x轴上的角的正切值不存在.( ) 解析:(1)因为根据三角函数在单位圆中的定义,可知 sin α=y=- ,所以(1)中说法正确. (2)终边在x轴上的角的正切值为0,故正切值存在.所以(2)中说 法错误. × 𝟐 𝟐

导航 2.正弦函数、余弦函数、正切函数在弧度制下的定义域 三角函数 定义域 y=sin x V-coSx y=tan x
导航 2.正弦函数、余弦函数、正切函数在弧度制下的定义域 三角函数 定义域 y=sin x R y=cos x R y=tan x 𝒙∈𝐑 𝒙 ≠ 𝒌𝛑 + 𝛑 𝟐 ,𝒌∈𝐙

导航 课堂·重难突破 三角函数定义的直接应用 典例剖析 1.在直角坐标系中,已知角a的终边与单位圆交于点A,点A的 纵坐标为,求tana
导航 课堂·重难突破 一 三角函数定义的直接应用 典例剖析 1.在直角坐标系中,已知角α的终边与单位圆交于点A,点A的 纵坐标为 ,求tan α. 𝟑 𝟓

导航 解:由题意,设点A的坐标为(x,) 所议斗图1,解得载号 时,an子 = 圣 354 当时,tana 3 4
导航 解:由题意,设点 A 的坐标为 𝒙, 𝟑 𝟓 , 所以 x 2 + 𝟑 𝟓 𝟐 =1,解得 x= 𝟒 𝟓 或 x=- 𝟒 𝟓 . 当 x= 𝟒 𝟓 时,tan α= 𝟑 𝟓 𝟒 𝟓 = 𝟑 𝟒 ; 当 x=- 𝟒 𝟓 时,tan α= 𝟑 𝟓 - 𝟒 𝟓 =- 𝟑 𝟒

二含参数的三角函数定义问题 导期 典例剖析 2已知角0的终边上有一点PV3,m,且sin0匠m,求cos0 与tan0的值. 解:由已知得点P到原点的距离=V3+mZ, 所以mr m 解得m-0或m=√5或m=√5. ①当m0时,P-V3,0,r=V3,cos0= -l1,tan0=0; 3
导航 二 含参数的三角函数定义问题 典例剖析 2.已知角 θ 的终边上有一点 P(- 𝟑,m), 且 sin θ = 𝟐𝟒 m,求 cos θ 与 tan θ 的值. 解:由已知得点 P 到原点的距离 r= 𝟑 + 𝒎 𝟐, 所以 𝟐𝟒 m= 𝒎 𝟑 + 𝒎 𝟐, 解得 m= 0 或 m= 𝟓 或 m=- 𝟓. ①当 m=0 时,P(- 𝟑,0),r= 𝟑,cos θ =- 𝟑 𝟑 =-1,tan θ =0;