
全程设计 第五章 三角函数 5.4 三确函数的图象与性质 5.4.3 正勿函数的性质与图象
第五章 三角函数 5.4 三角函数的图象与性质 5.4.3 正切函数的性质与图象

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破
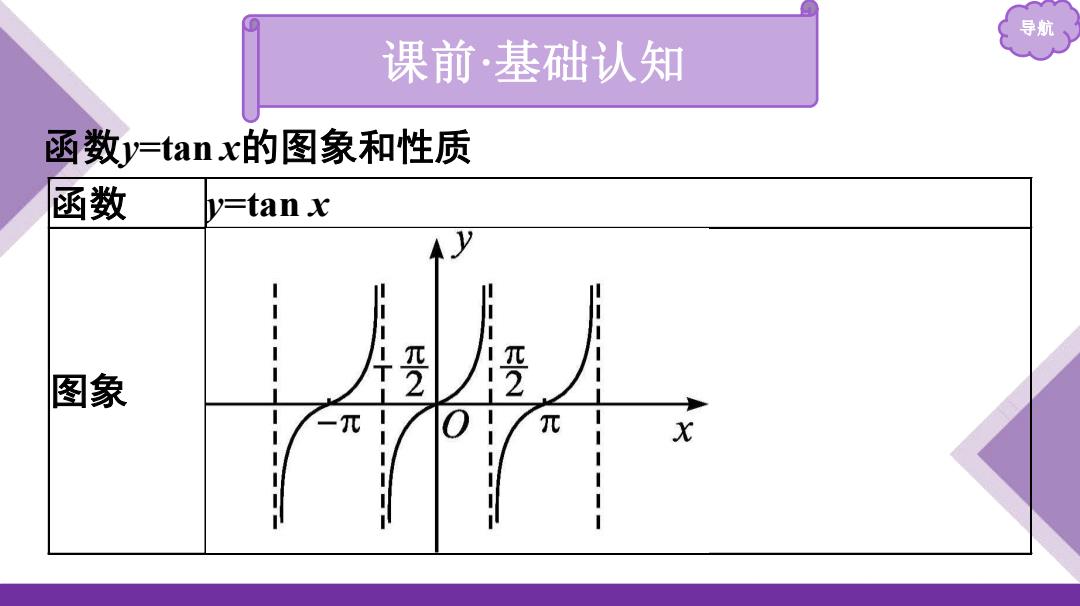
导航 课前·基础认知 函数y=tanx的图象和性质 函数 v=tan x 图象 L 一元 0 X 1
导航 课前 ·基础认知 函数y=tan x的图象和性质 函数 y=tan x 图象

导航 函数 y=tan x 定义域 值域 周期性 正切函数是周期函数,周期是 奇偶性 正切函数是 函数 在每一个区间 内都单 单调性 调递增
导航 函数 y=tan x 定义域 𝐱 𝐱∈𝐑,且𝒙 ≠ 𝛑 𝟐 + 𝒌𝛑,𝒌∈𝐙 值域 R 周期性 正切函数是周期函数,周期是 π 奇偶性 正切函数是 奇 函数 单调性 在每一个区间 𝒌𝛑- 𝛑 𝟐 ,𝒌𝛑 + 𝛑 𝟐 (k∈Z) 内都单 调递增

导航 微点拨对于正切曲线的理解 ()正切曲线的特征 正切曲线是由与y轴平行的一系列直线x=红+化∈Z)所隔开 的无穷多支形状相同的曲线组成的,并沿轴的上、下两个方 向无限伸展
导航 微点拨 对于正切曲线的理解 (1)正切曲线的特征 正切曲线是由与y轴平行的一系列直线x=kπ+ (k∈Z)所隔开 的无穷多支形状相同的曲线组成的,并沿y轴的上、下两个方 向无限伸展. 𝛑 𝟐

导航 2由正切函数的图象可知,正切函数的图象关于点(,0),k ∈Z成中心对称,因此,正切函数图象的对称中心为(,0),k ∈Z正切函数的图象不是轴对称图形,不存在对称轴,但存在 无数条相互平行的渐近线x2+km,k∈Z
导航 (2)由正切函数的图象可知,正切函数的图象关于点 𝒌𝛑 𝟐 ,𝟎 ,k ∈Z 成中心对称,因此,正切函数图象的对称中心为 𝒌𝛑 𝟐 ,𝟎 ,k ∈Z.正切函数的图象不是轴对称图形,不存在对称轴,但存在 无数条相互平行的渐近线:x= 𝛑 𝟐 +kπ,k∈Z

导航 微思考正切函数在定义域内是增函数吗? 提示:不是,在每个单独区间(k-2,kπ+)k∈Z)内都单调 递增,但在整个定义域内不是增函数,如180°>30°,但 tan180°=0<tan30°-3 1
导航 微思考 正切函数在定义域内是增函数吗? 提示:不是,在每个单独区间 𝒌𝛑- 𝛑 𝟐 ,𝒌𝛑 + 𝛑 𝟐 (k∈Z)内都单调 递增,但在整个定义域内不是增函数,如 180°>30°,但 tan 180°=0<tan 30°= 𝟑 𝟑

导航 微训练 (山)函数f)=2tan(x+3)的最小正周期为( A.2元 B.4元 C.2 D.4 (2)函数y=tanx的图象与直线Jy=1相邻两个交点之间的距离 是( A好 B c D.元
导航 微训练 (1)函数 f(x)=2tan 𝛑 𝟐 𝒙 + 𝟑 的最小正周期为( ) A.2π B.4π C.2 D.4 (2)函数 y=|tan x|的图象与直线 y=1 相邻两个交点之间的距离 是( ) A. 𝛑 𝟒 B. 𝛑 𝟑 C. 𝛑 𝟐 D.π

导航 答案:1)C(2)C 解析:(山)函数fx)=2tan(x+3)的最小正周期为四=2故选C (2)函数y=tan的最小正周期为元,由tan=1得,=km±k ∈Z),所以函数Jy=tanx的图象与直线y=1相邻两个交点之间 的距离为函数tanx的半个最小正周期,即空
导航 答案 :(1)C (2)C 解析:(1)函数 f(x)=2tan 𝛑𝟐 𝒙 + 𝟑 的最小正周期为 𝛑𝛑𝟐 = 2.故选 C. (2)函数 y=|tan x|的最小正周期为 π,由|tan x|=1 得,x=kπ ± 𝛑𝟒(k ∈ Z),所以函数 y=|tan x|的图象与直线 y=1 相邻两个交点之间 的距离为函数 y=|tan x|的半个最小正周期,即 𝛑𝟐

导航 课堂·重难突破 正切函数的定义域、值域问题 典例剖析 1.()函数,=3tan(丑)的定义域 为 2)函数)=tan(2x)》x∈(是,Z)的值域 是
导航 课堂·重难突破 一 正切函数的定义域、值域问题 典例剖析 1.(1)函数 y=3tan 𝛑 𝟔 - 𝒙 𝟒 的定义域 为 ; (2)函数 y=tan 𝟐𝒙- 𝛑 𝟑 ,x∈ - 𝛑 𝟏𝟐 , 𝟕𝛑 𝟐𝟒 的值域 是