
全程设计 第四章 指数数与对数数 4.4对数函数 第2课时 对数函数的图象与性质
第四章 指数函数与对数函数 4.4 对数函数 第2课时 对数函数的图象与性质

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破
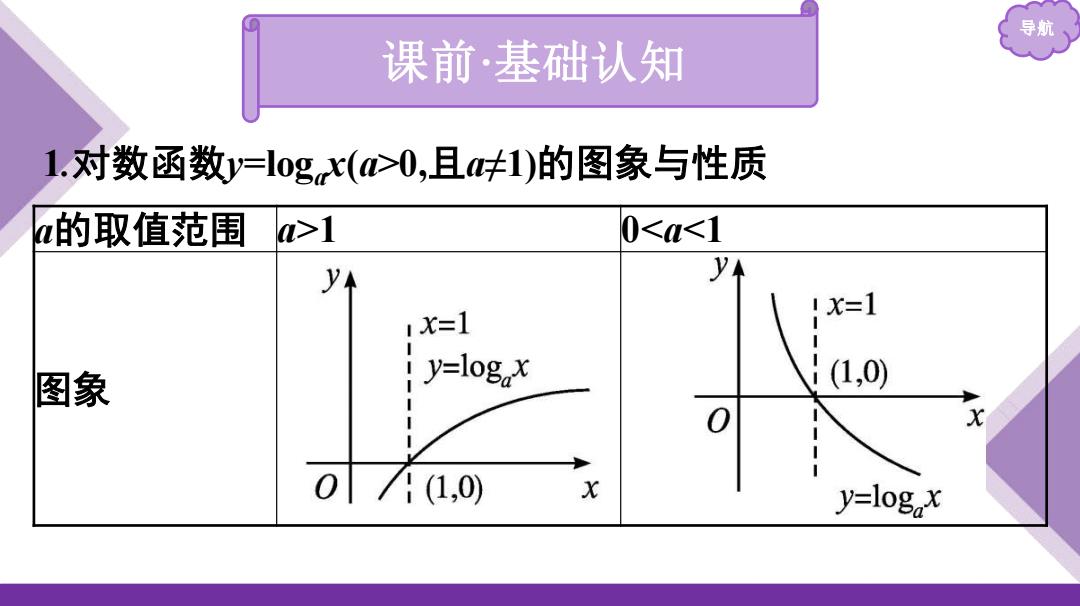
导航、 课前·基础认知 1.对数函数y=logx(a心>0,且呋1)的图象与性质 的取值范围 a>1 0<a<1 A y !x=1 1x=1 图象 y=logx (1,0) 0 071(1,0) X y=log x
导航 课前·基础认知 1.对数函数y=logax(a>0,且a≠1)的图象与性质 a的取值范围 a>1 0<a<1 图象

导航 的取值范围 a>1 01时, 当x>1时, 质 在区间0,+o)内是 在区间(0,+∞)内是 单调性
导航 a的取值范围 a>1 01时, y>0 当00 当x>1时, y<0 单调性 在区间(0,+∞)内是 增函数 在区间(0,+∞)内是 减函数

导航 2.反函数 般地,指数函数y=(>0,且呋1)与对数函数y=logx(>0,且 呋1)互为 ,它们的定义域与值域正好 微拓展并不是任何一个函数y=f),都有反函数只有定义域 和值域满足一一对应的函数才有反函数
导航 2.反函数 一般地,指数函数y=ax (a>0,且a≠1)与对数函数y=logax(a>0,且 a≠1)互为 反函数 ,它们的定义域与值域正好 互换 . 微拓展 并不是任何一个函数y=f(x),都有反函数.只有定义域 和值域满足一一对应的函数才有反函数

导航 课堂·重难突破 比较对数值的大小 典例剖析 1.(1)已知x∈(亏,1),=lnx,b=2lnx,c=(lnx)3,那么( A.a0,且呋1)( A.log 5.1l0g12.2 C.log1(a+1)<log1.a D.log32.9<l0g.s2.2
导航 课堂·重难突破 一 比较对数值的大小 典例剖析 1.(1)已知x∈( ,1),a=ln x,b=2ln x,c=(ln x) 3 ,那么( ) A.a0,且a≠1)( ) A.loga5.1lo𝐠𝟏 𝟐 2.2

导 答案:1)C(2)B 解析:(1.x∈(1,.∴-lnx∈(1,0,则b=2nx=lnx2In x=a,.'.b0,l0g0.52.2<0,故不成 立.故选B
导航 答案:(1)C (2)B 解析:(1)∵x∈( ,1),∴a=ln x∈(-1,0),则b=2ln x=ln x 2ln x=a,∴b0,log0.52.2<0,故不成 立.故选B. 𝟏 𝟐 𝟏 𝟐

导航 规律总结 比较对数值大小时常用的四种方法 (1)同底数的利用对数函数的单调性 (2)同真数的利用对数函数的图象或用换底公式转化. 3)底数和真数都不同,找中间量. (4)若底数为同一参数,则根据底数对对数函数单调性的影响 对底数进行分类讨论
导航 比较对数值大小时常用的四种方法 (1)同底数的利用对数函数的单调性. (2)同真数的利用对数函数的图象或用换底公式转化. (3)底数和真数都不同,找中间量. (4)若底数为同一参数,则根据底数对对数函数单调性的影响, 对底数进行分类讨论

导航 二 简单的对数型不等式的解法 典例剖析 2.()已知l0g21,则u的取值范围为 (2)己知l0g0.7(2x)l1og3,则a的取值范围为
导航 二 简单的对数型不等式的解法 典例剖析 2.(1)已知 log a 𝟏𝟐 >1, 则 a 的取值范围为 . (2)已知log 0.7(2 x)1>lo 𝐠 𝟑𝟒 a,则 a 的取值范围为

导 答案:(山)(21) 21,+o)(3(,1)④(1 解析:(1)由题意可知,>0,且呋1. 当心1时,函数lgx为增函数,且log1=log,所以0<< 与心1矛盾,故舍去;当0<<1时,函数y=l0gx为减函数,由 log71=log,得a心2所以<1.综上,a的取值范围为2<1
导航 答案:(1) 𝟏 𝟐 ,1 (2)(1,+∞) (3) 𝟐 𝟐 ,1 (4) 𝟑 𝟒 ,1 解析:(1)由题意可知,a>0,且 a≠1. 当a>1时,函数y=logax为增函数,且loga 𝟏 𝟐 >1=logaa,所以01 矛盾,故舍去;当 01=logaa,得 a> 𝟏 𝟐 ,所以𝟏 𝟐 <a<1.综上,a 的取值范围为𝟏 𝟐 <a<1