
全程设计 6.3.4 平面向量数乘运算的坐标表示
6.3.4 平面向量数乘运算的坐标表示

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 1.平面向量数乘运算的坐标表示 (1)符号表示:已知=x,),则= (2)文字描述:实数与向量的积的坐标等于用这个实数乘原 来向量的相应坐标 2.平面向量共线的坐标表示 设=(化1y1),b=(化2y2),其中b≠0,,b共线的充要条件是
导航 课前·基础认知 1.平面向量数乘运算的坐标表示 (1)符号表示:已知a=(x,y),则λa= (λx,λy) . (2)文字描述:实数与向量的积的坐标等于用这个实数乘原 来向量的相应坐标. 2.平面向量共线的坐标表示 设a=(x1 ,y1 ),b=(x2 ,y2 ),其中b≠0,a,b共线的充要条件是 x1 y2 -x2 y1 =0

导月 微思考两向量=化1y1),b=(化2y2)共线的坐标条件能表示成 x1y1吗? x2 y2 提示:不能.当x2y2有一者为零时,比例式没有意义,只有当 x2y20时,才能使用. 3.中点坐标公式 若点P1,P2的坐标分别为c1y1),(化2y2,线段P1P2的中点P的坐 X1+X2 标为化y),则 2 v= y1+y2 2
导航 微思考 两向量a=(x1 ,y1 ),b=(x2 ,y2 )共线的坐标条件能表示成 吗? 提示:不能.当x2 ,y2有一者为零时,比例式没有意义,只有当 x2 y2≠0时,才能使用. 3.中点坐标公式 若点P1 ,P2的坐标分别为(x1 ,y1 ),(x2 ,y2 ),线段P1P2的中点P的坐 标为(x,y),则 𝒙𝟏 𝒙𝟐 = 𝒚𝟏 𝒚𝟐 𝒙 = 𝒙𝟏 + 𝒙𝟐 𝟐 , 𝒚 = 𝒚𝟏 + 𝒚𝟐 𝟐

导航 课堂·重难突破 向量共线的判定与证明 典例剖析 1.(1)下列各组向量中,共线的是(D) A.=(-2,3),b=(4,6)B.=(2,3),b=(3,2) C.=(1,-2),b=(7,14)D.=(-3,2),b=(6,-4) 解析:A中,-2×6-3×4≠0;B中,3×3-2×2≠0;C中,1X14-( 2)×7≠0;D中,(-3)×(-4)-2×6=0.故选D
导航 课堂·重难突破 一 向量共线的判定与证明 典例剖析 1.(1)下列各组向量中,共线的是( ) A.a=(-2,3),b=(4,6) B.a=(2,3),b=(3,2) C.a=(1,-2),b=(7,14) D.a=(-3,2),b=(6,-4) 解析:A中,-2×6-3×4≠0;B中,3×3-2×2≠0;C中,1×14-(- 2)×7≠0;D中,(-3)×(-4)-2×6=0.故选D. D

导航 (2)已知A(-1,-1),B(1,3),C1,5),D(2,7),向量AB与CD平行吗?直线 AB平行于直线CD吗? 解:.AB=(2,4),CD=(1,2),又2×2-4×1=0,.AB∥CD. 又AC=(2,6),AB=(2,4),∴.2×4-2×60,∴.A,B,C三点不共线, ∴.直线AB与直线CD不重合,.AB∥CD
导航 (2)已知 A(-1,-1),B(1,3),C(1,5),D(2,7),向量𝑨 𝑩 与𝑪 𝑫 平行吗?直线 AB 平行于直线 CD 吗? 解:∵𝑨 𝑩 =(2,4),𝑪 𝑫 =(1,2),又 2×2-4×1=0,∴𝑨 𝑩 ∥𝑪 𝑫 . 又𝑨 𝑪 =(2,6),𝑨 𝑩 =(2,4),∴2×4-2×6≠0,∴A,B,C 三点不共线, ∴直线 AB 与直线 CD 不重合,∴AB∥CD
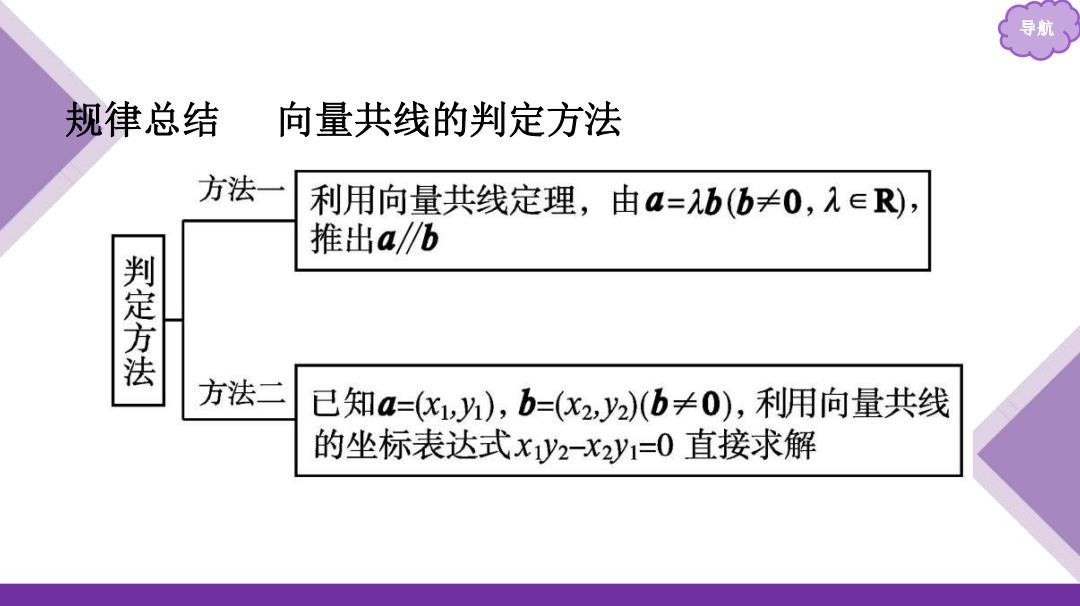
导航 规律总结 向量共线的判定方法 方法一 利用向量共线定理,由a=λb(b≠0,1∈R), 推出ab 判定方法 方法二 已知a=(K,),b=(x2,y2)(b≠0),利用向量共线 的坐标表达式xy2-x2y1=0直接求解
导航 规律总结 向量共线的判定方法

导航 二向量共线的综合应用 典例剖析 2.(1)已知向量=(cosa,-2),b=(sina,1),且a∥b,则2 sinacosa等 于(C) A.3 B.-3 c号 D 解析:因为a∥b,所以cos ax1-(-2)sina=0,即cosa=-2sina,故 tana-2,所以2sina0sa 2sinacosa 2tang 2×(2) sin2a+cos2a tan2a+1 ()+1 5
导航 二 向量共线的综合应用 典例剖析 2.(1)已知向量a=(cosα,-2),b=(sinα,1),且a∥b,则2sinαcosα等 于( ) A.3 B.-3 C.- 𝟒 𝟓 D.𝟒 𝟓 解析:因为 a∥b,所以 cos α×1-(-2)×sin α=0,即 cos α=-2sin α,故 tan α=- 𝟏 𝟐 ,所以 2sin αcos α= 𝟐𝐬𝐢𝐧𝜶𝐜𝐨𝐬𝜶 𝐬𝐢𝐧 𝟐 𝜶+𝐜𝐨𝐬 𝟐 𝜶 = 𝟐𝐭𝐚𝐧𝜶 𝐭𝐚𝐧 𝟐 𝜶+𝟏 = 𝟐× - 𝟏 𝟐 - 𝟏 𝟐 𝟐 +𝟏 =- 𝟒 𝟓 . C
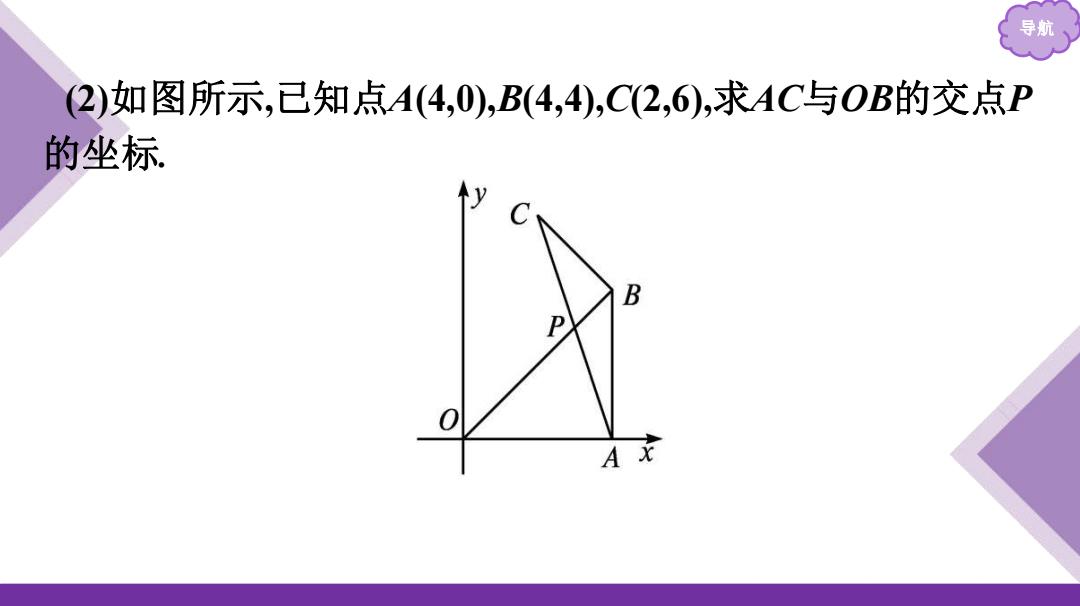
导航 2)如图所示,已知点A(4,0),B(4,4),C2,6),求AC与OB的交点P 的坐标 B A
导航 (2)如图所示,已知点A(4,0),B(4,4),C(2,6),求AC与OB的交点P 的坐标

导航 解:方法一:(定理法)由O,P,B三点共线, 可设0P=20B=(42,42)2∈R), 则AP=0P0A=(41-4,4),AC=0C-0A=(-2,6) 由AP与AC共线得(41-4)x6-4x(-2)0,解得2- 所以0P=0B-(3,3),所以点P的坐标为3,3)
导航 解:方法一:(定理法)由 O,P,B 三点共线, 可设𝑶 𝑷 =λ𝑶 𝑩 =(4λ,4λ)(λ∈R), 则𝑨 𝑷 = 𝑶 𝑷 -𝑶 𝑨 =(4λ-4,4λ),𝑨 𝑪 = 𝑶 𝑪 -𝑶 𝑨 =(-2,6). 由𝑨 𝑷 与𝑨 𝑪 共线得(4λ-4)×6-4λ×(-2)=0,解得 λ= 𝟑 𝟒 , 所以𝑶 𝑷 = 𝟑 𝟒 𝑶 𝑩 =(3,3),所以点 P 的坐标为(3,3)