
全程设计 7.1.1 数系的扩充和复数的概念
7.1.1 数系的扩充和复数的概念

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 1,复数的有关概念 (1)定义:我们把形如+bi(a,b∈R)的数叫做复数,其中i叫做 ,全体复数所构成的集合C={+bia,b∈R叫做 (2)复数通常用字母 表示,即=叶bi(a,b∈R),其中的a与b 分别叫做复数z的实部与虚部. 2.复数相等的充要条件 设a,b,c,d都是实数,那么a+bi=c+i当且仅当
导航 课前·基础认知 1.复数的有关概念 (1)定义:我们把形如a+bi(a,b∈R)的数叫做复数,其中i叫做 虚数单位 .全体复数所构成的集合C={a+bi|a,b∈R}叫做 复数集 . (2)复数通常用字母 z 表示,即z=a+bi(a,b∈R),其中的a与b 分别叫做复数z的实部与虚部. 2.复数相等的充要条件 设a,b,c,d都是实数,那么a+bi=c+di当且仅当a=c且b=d

微探究1由3>2能否推出3+>2+i?两个实数能比较大小,那 么两个复数能比较大小吗? 提示:由3>2不能推出3+>2+i,当两个复数都是实数时,可以 比较大小,当两个复数不全是实数时,不能比较大小 微探究2若复数z=+bi>0,则实数a,b满足什么条件? 提示:若复数z=叶bi>0,则实数a,b满足心>0,且b=0
导航 微探究1 由3>2能否推出3+i>2+i?两个实数能比较大小,那 么两个复数能比较大小吗? 提示:由3>2不能推出3+i>2+i,当两个复数都是实数时,可以 比较大小,当两个复数不全是实数时,不能比较大小. 微探究2 若复数z=a+bi>0,则实数a,b满足什么条件? 提示:若复数z=a+bi>0,则实数a,b满足a>0,且b=0
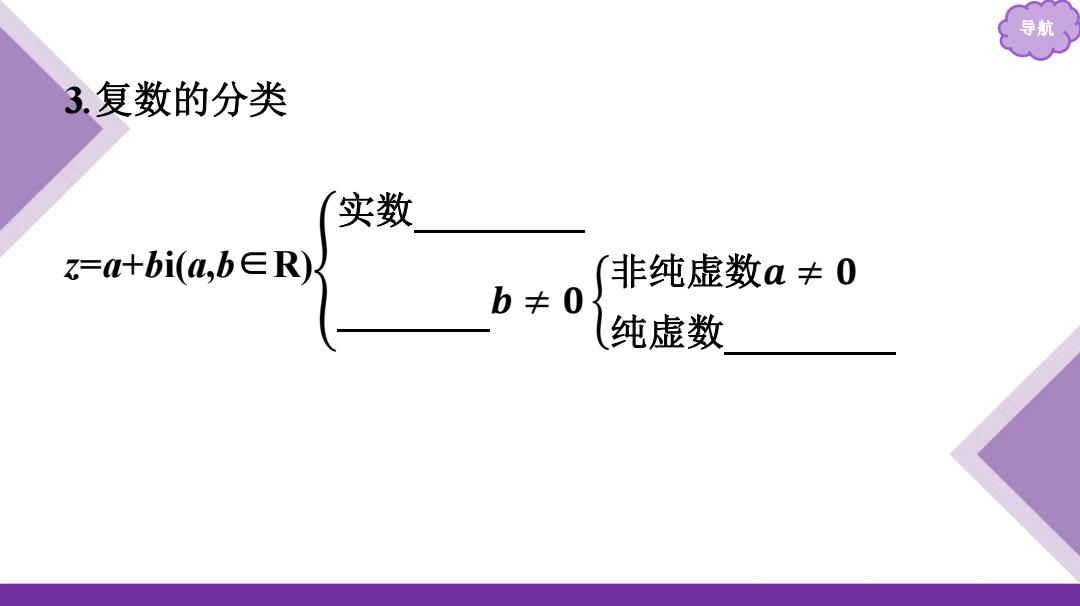
导航 3.复数的分类 实数 Z=+bi(a,b∈R) T非纯虚数a≠0 b≠0 纯虚数
导航 3 .复数的分类 z = a + bi( a , b ∈R) 实数 𝒃 = 𝟎 虚数 𝒃 ≠ 𝟎 非纯虚数 𝒂 ≠ 𝟎 纯虚数 𝒂 = 𝟎
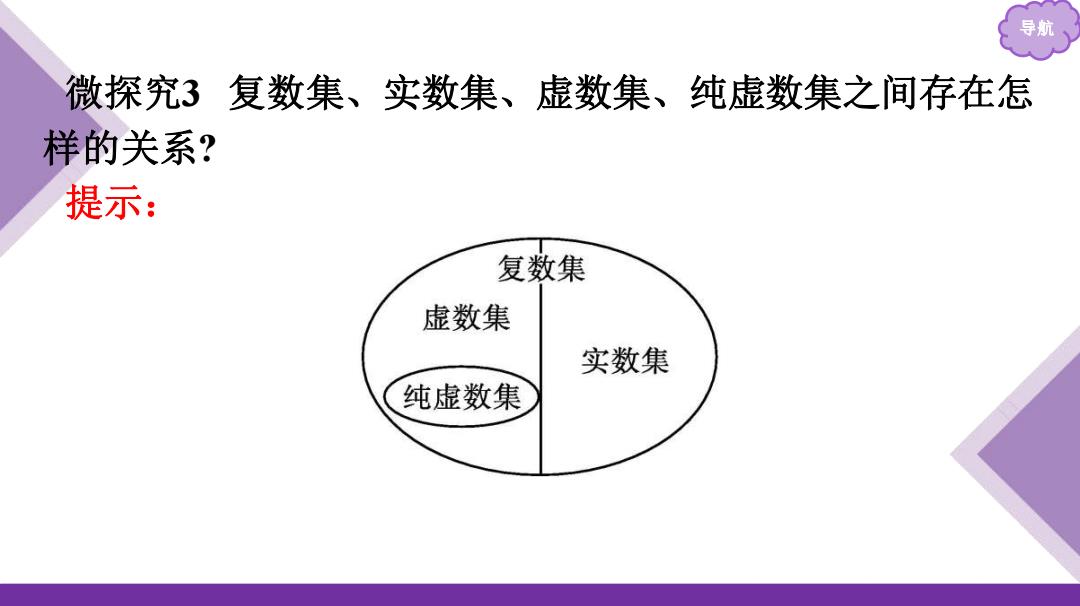
导航 微探究3复数集、实数集、虚数集、纯虚数集之间存在怎 样的关系? 提示: 复数集 虚数集 实数集 纯虚数集
导航 微探究3 复数集、实数集、虚数集、纯虚数集之间存在怎 样的关系? 提示:

导航 课堂·重难突破 复数的概念 典例剖析 1.给出下列说法:①复数2+3的虚部是3i;②形如+bi(b∈R) 的数一定是虚数;③若a∈R,0,则(+3)i是纯虚数;④若两个 复数能够比较大小,则它们都是实数其中错误说法的个数是 (C) A.1 B.2 C.3 D.4
导航 课堂·重难突破 一 复数的概念 典例剖析 1.给出下列说法:①复数2+3i的虚部是3i;②形如a+bi(b∈R) 的数一定是虚数;③若a∈R,a≠0,则(a+3)i是纯虚数;④若两个 复数能够比较大小,则它们都是实数.其中错误说法的个数是 ( ) A.1 B.2 C.3 D.4 C

导航 解析:复数2+3i的虚部是3,①错;形如a+bi(b∈R)的数不一 定是虚数,②错;只有当a∈R,+3≠0时,(+3)i是纯虚数,③错;若 两个复数能够比较大小,则它们都是实数,故④正确,所以错误 说法有3个
导航 解析:复数2+3i的虚部是3,①错;形如a+bi(b∈R)的数不一 定是虚数,②错;只有当a∈R,a+3≠0时,(a+3)i是纯虚数,③错;若 两个复数能够比较大小,则它们都是实数,故④正确,所以错误 说法有3个

导航 规律总结判断复数概念方面的命题真假的注意点 ()正确理解复数、虚数、纯虚数、实部、虚部、复数相等 的概念,注意它们之间的区别与联系; (2)注意复数集与实数集中有关概念与性质的不同; 3)注意通过列举反例来判断一些命题的真假
导航 规律总结 判断复数概念方面的命题真假的注意点 (1)正确理解复数、虚数、纯虚数、实部、虚部、复数相等 的概念,注意它们之间的区别与联系; (2)注意复数集与实数集中有关概念与性质的不同; (3)注意通过列举反例来判断一些命题的真假

导航 二复数的分类 典例剖析 2.己知复数z= 2-x-6+2-2x-15)1,当z分别满足下列条件时, X+3 求实数x的值 (1)z是实数; (2)z是虚数; 3)z是纯虚数
导航 二 复数的分类 典例剖析 2.已知复数z= +(x 2 -2x-15)i,当z分别满足下列条件时, 求实数x的值. (1)z是实数; (2)z是虚数; (3)z是纯虚数. 𝒙 𝟐 -𝒙-𝟔 𝒙 + 𝟑