
全程设计 8.5.3 平面与平面平行
8.5.3 平面与平面平行

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 1.平面与平面平行的判定定理 文字语言 图形语言 符号语言 如果一个平面内的 与 aCB,bCB,anb 另一个平面平行,那 =P,a∥a,b∥ 么这两个平面平行 a→B1∥a
导航 课前·基础认知 1.平面与平面平行的判定定理 文字语言 图形语言 符号语言 如果一个平面内的 两条相交直线 与 另一个平面平行,那 么这两个平面平行 a⊂β,b⊂β,a∩b =P,a∥α,b∥ α⇒β∥α

导航 微思考1判定定理中的“相交”能否去掉? 提示:不能,如果是一个平面内的两条平行直线与另一个平 面平行,那么这两个平面也可能相交
导航 微思考1 判定定理中的“相交”能否去掉? 提示:不能,如果是一个平面内的两条平行直线与另一个平 面平行,那么这两个平面也可能相交
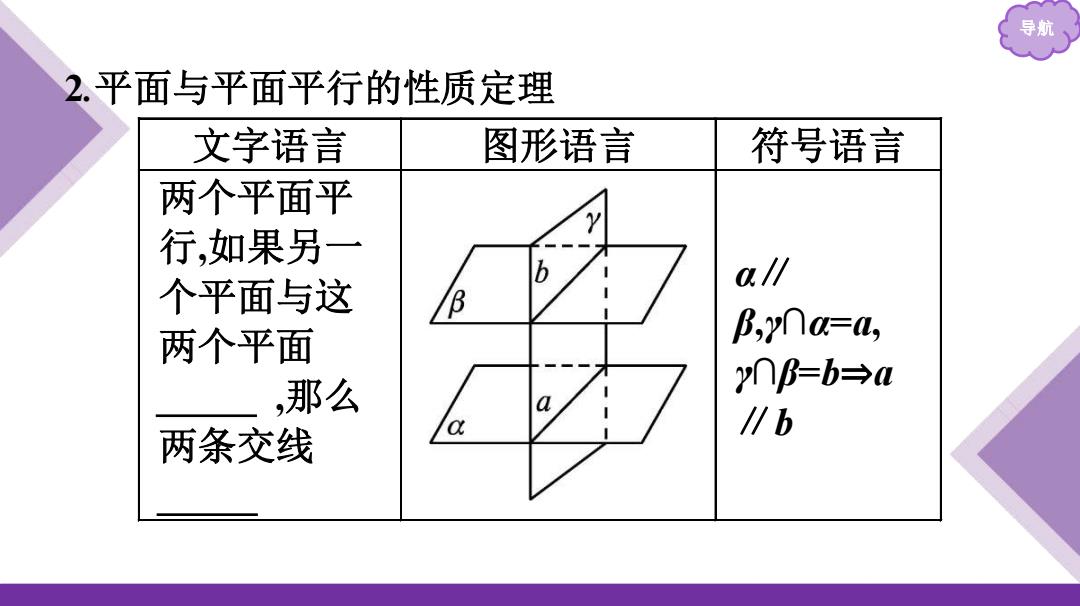
导航 2.平面与平面平行的性质定理 文字语言 图形语言 符号语言 两个平面平 行,如果另一 个平面与这 a∥ B 两个平面 B,y∩=a, ,那么 ynB=b→a C ∥b 两条交线
导航 2 .平面与平面平行的性质定理 文字语言 图形语言 符号语言 两个平面平 行,如果另一 个平面与这 两个平面 相交 ,那么 两条交线 平行 α ∥ β,γ∩ α = a, γ∩β=b⇒a ∥b

导航 微思考2分别位于两个平行平面内的两条直线有什么位置 关系? 提示:分别位于两个平行平面内的两条直线一定无公共点, 故它们的位置关系是平行或异面
导航 微思考2 分别位于两个平行平面内的两条直线有什么位置 关系? 提示:分别位于两个平行平面内的两条直线一定无公共点, 故它们的位置关系是平行或异面

微拓展1常用的面面平行的其他几个性质 两个平面平行,其中一个平面内的任意一条直线平行于另 一个平面. 2)夹在两个平行平面之间的平行线段长度相等 3)经过平面外一点有且只有一个平面与已知平面平行. (4)两条直线被三个平行平面所截,截得的对应线段成比例: (⑤)如果两个平面分别平行于第三个平面,那么这两个平面互 相平行!
导航 微拓展1 常用的面面平行的其他几个性质 (1)两个平面平行,其中一个平面内的任意一条直线平行于另 一个平面. (2)夹在两个平行平面之间的平行线段长度相等. (3)经过平面外一点有且只有一个平面与已知平面平行. (4)两条直线被三个平行平面所截,截得的对应线段成比例. (5)如果两个平面分别平行于第三个平面,那么这两个平面互 相平行
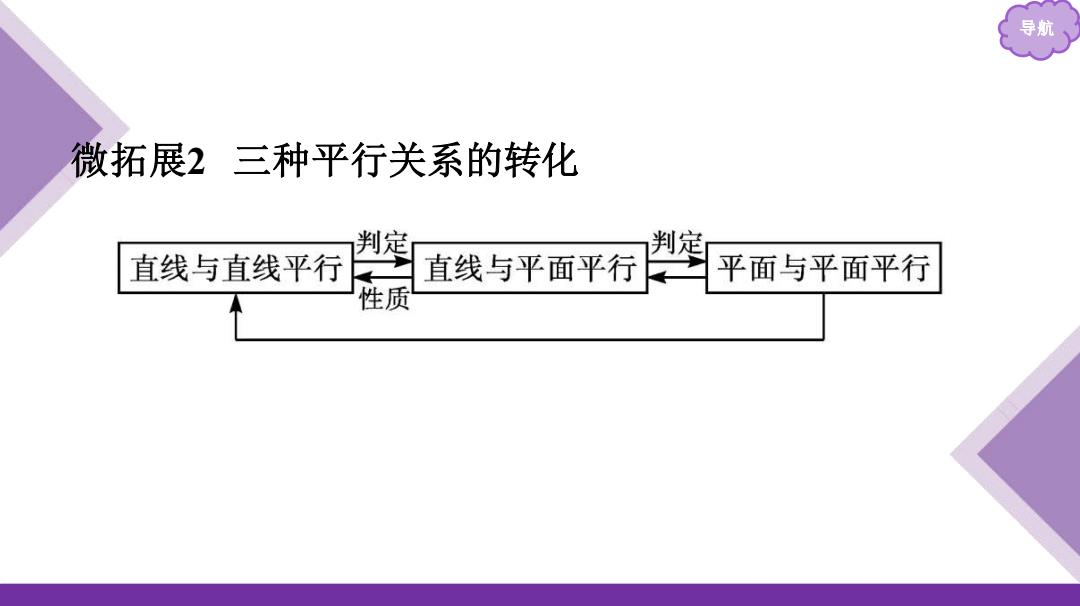
导航 微拓展2三种平行关系的转化 判定 判定 直线与直线平行 直线与平面平行 平面与平面平行 性质
导航 微拓展2 三种平行关系的转化

导航 课堂·重难突破 平面与平面平行的判定 典例剖析 1如图,在正方体ABCD-A1B1C1D1中,M,E,F,N分别是 A1B1,B1C1,C1D1,D1A1的中点 求证:(1)E,F,B,D四点共面; A B (2)平面MAN∥平面EFDB. N Ai M
导航 课堂·重难突破 一 平面与平面平行的判定 典例剖析 1.如图,在正方体ABCD-A1B1C1D1中,M,E,F,N分别是 A1B1 ,B1C1 ,C1D1 ,D1A1的中点. 求证:(1)E,F,B,D四点共面; (2)平面MAN∥平面EFDB
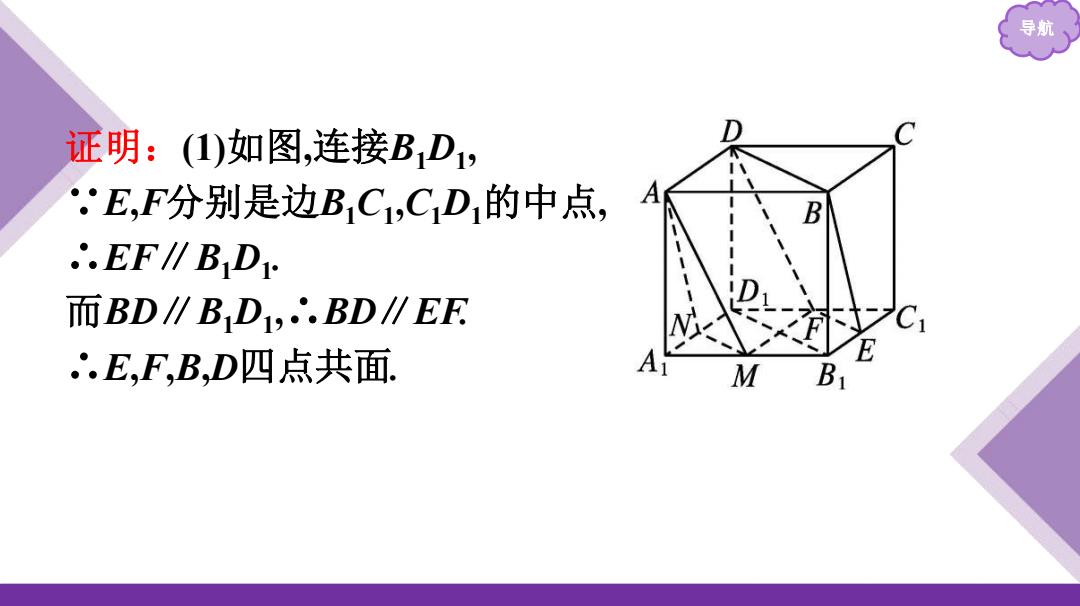
导航 证明:(1)如图,连接BD1, D .E,F分别是边BC1,CD1的中点, A ∴.EF∥BD1 而BD∥BD,.BD∥EF .E,F,B,D四点共面 M B
导航 证明:(1)如图 ,连接 B 1 D 1 , ∵ E , F分别是边B 1 C1 , C1 D 1的中点 , ∴EF ∥ B 1 D 1 . 而BD ∥ B 1 D 1 , ∴BD ∥EF. ∴ E , F, B ,D四点共面