
全程设计 1.3 空间向量及其运算的坐标表示 1.3.1 空间直角坐标系
1.3 空间向量及其运算的坐标表示 1.3.1 空间直角坐标系
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
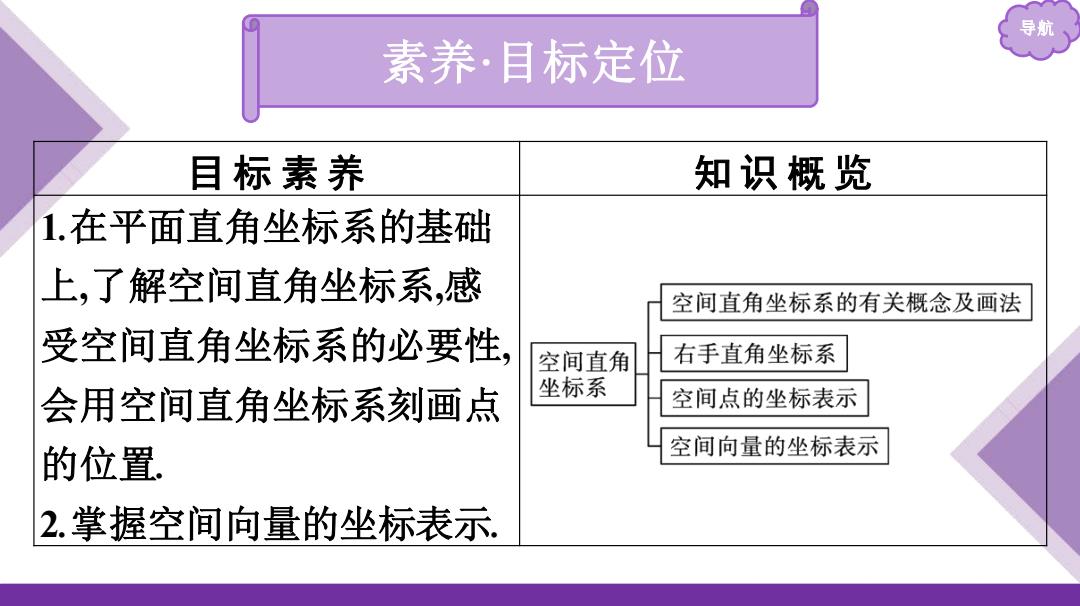
导航 素养·目标定位 目标素养 知识概览 1.在平面直角坐标系的基础 上,了解空间直角坐标系,感 空间直角坐标系的有关概念及画法 受空间直角坐标系的必要性, 空间直角 右手直角坐标系 会用空间直角坐标系刻画点 坐标系 空间点的坐标表示 的位置 空间向量的坐标表示 2.掌握空间向量的坐标表示
导航 素养·目标定位 目 标 素 养 知 识 概 览 1.在平面直角坐标系的基础 上,了解空间直角坐标系,感 受空间直角坐标系的必要性, 会用空间直角坐标系刻画点 的位置. 2.掌握空间向量的坐标表示

导期 课前·基础认知 1.空间直角坐标系 在空间选定一点O和一个单位正交基底{ij,k}.以点O为原点, 分别以i,,k的方向为正方向、以它们的长为单位长度建立三 条数轴: ,它们都叫做坐标轴这时我们就建 立了一个空间直角坐标系Oxz,O叫做原点,ij,k都叫做坐标向 量,通过每两条坐标轴的平面叫做坐标平面,分别称为 平面, 平面, 平面,它们把空间分成了八个部 分
导航 课前·基础认知 1.空间直角坐标系 在空间选定一点O和一个单位正交基底{i,j,k}.以点O为原点, 分别以i,j,k的方向为正方向、以它们的长为单位长度建立三 条数轴: x轴、y轴、z轴 ,它们都叫做坐标轴.这时我们就建 立了一个空间直角坐标系Oxyz,O叫做原点,i,j,k都叫做坐标向 量,通过每两条坐标轴的平面叫做坐标平面,分别称为 Oxy 平面, Oyz 平面, Ozx 平面,它们把空间分成了八个部 分

导期 画法:画空间直角坐标系Oxz时,一般使∠xOy=或 ,∠yOz= 2.右手直角坐标系 在空间直角坐标系中,让右手拇指指向 的正方向,食指 指向 的正方向,如果中指指向 的正方向,则称 这个坐标系为右手直角坐标系
导航 画法:画空间直角坐标系Oxyz时,一般使∠xOy= 135° (或 45° ),∠yOz= 90° . 2.右手直角坐标系 在空间直角坐标系中,让右手拇指指向 x轴 的正方向,食指 指向 y轴 的正方向,如果中指指向 z轴 的正方向,则称 这个坐标系为右手直角坐标系

3.空间点的坐标表示 在空间直角坐标系Oxz中,ij,k为坐标向量,对空间任意一点 A,对应一个向量OA,且点A的位置由向量OA唯一确定,由空间 向量基本定理,存在唯一的有序实数组(x,y,),使0A= 在单位正交基底{i,j,k}下与向量OA对应的 叫做点A在空间直角坐标系中的坐标,记作 ,其中 叫做点A的横坐标,叫做点A的纵 坐标, 叫做点A的竖坐标
导航 3 .空间点的坐标表示 在空间直角坐标系 Oxyz 中,i,j,k 为坐标向量,对空间任意一点 A,对应一个向量 𝑂 𝐴 ,且点 A 的位置由向量 𝑂 𝐴 唯一确定,由空间 向量基本定理,存在唯一的有序实数组(x,y,z), 使 𝑂 𝐴 = xi+yj+z k .在单位正交基底{i,j,k}下与向量 𝑂 𝐴 对应的 有序 实数组(x,y,z) ,叫做点 A 在空间直角坐标系中的坐标,记作 A(x,y,z) ,其中 x 叫做点 A 的横坐标, y 叫做点 A 的纵 坐标, z 叫做点 A 的竖坐标

导航 微思考在给定的空间直角坐标系中,空间任意一点是否与有 序实数组心y,z)存在唯一的对应关系? 提示:是
导航 微思考在给定的空间直角坐标系中,空间任意一点是否与有 序实数组(x,y,z)存在唯一的对应关系? 提示:是

导航 4.空间向量的坐标表示 在空间直角坐标系Oxyz中,给定向量a,作0A=a.由空间向量 基本定理,存在唯一的有序实数组(x,y,z),使a= 有序实数组(x,y,z)叫做a在空间直角坐标系Oxyz中的坐标,上 式可简记作a=
导航 4.空间向量的坐标表示 在空间直角坐标系Oxyz中,给定向量a,作 =a.由空间向量 基本定理,存在唯一的有序实数组(x,y,z),使a= xi+yj+zk . 有序实数组(x,y,z)叫做a在空间直角坐标系Oxyz中的坐标,上 式可简记作a= (x,y,z) . 𝑂 𝐴

导航 课堂·重难突破 空间点、向量的坐标表示 典例剖析 1.如图,在直三棱柱ABC-A1B,C1 B 中,CA=CB=1,∠BCA=90°,棱AA1=2,M,N分别为 M AB1,AA的中点,试建立适当的坐标系,求: N (1)点B,C1,B1,M,N的坐标; (2)向量BN,BA,A1B的坐标
导航 课堂·重难突破 一 空间点、向量的坐标表示 典例剖析 1.如图,在直三棱柱ABC-A1B1C1 中,CA=CB=1,∠BCA=90° ,棱AA1 =2,M,N分别为 A1B1 ,A1A的中点,试建立适当的坐标系,求: (1)点B,C1 ,B1 ,M,N的坐标; (2)向量𝑩 𝑵 , 𝑩𝑨𝟏 ,𝑨 𝟏 𝑩 的坐标

解:.CC1⊥AC,CC1⊥BC,AC⊥BC,且CA=CB=1,CC1=2, 以{CA,C丽,CC为单位正交基底,建立空间直角坐标系 Cxyz,如图所示. (1),点B在y轴上,且CB=1,所以CB=0i+j+0k 所以点B的坐标是(0,1,0) 同理,点C1的坐标是(0,0,2), 点B,在x轴、y轴、z轴上的射影分别为C,B,C1,它们在坐标轴 上的坐标分别为0,1,2,所以点B的坐标是(0,1,2)
导航 解:∵CC1⊥AC,CC1⊥BC,AC⊥BC,且CA=CB=1,CC1 =2, ∴以 𝐶 𝐴 ,𝐶 𝐵 , 1 2 𝐶𝐶1 为单位正交基底,建立空间直角坐标系 Cxyz,如图所示. (1)点 B 在 y 轴上,且 CB=1,所以𝐶 𝐵 =0i+j+0k. 所以点B的坐标是(0,1,0). 同理,点C1的坐标是(0,0,2). 点B1在x轴、y轴、z轴上的射影分别为C,B,C1 ,它们在坐标轴 上的坐标分别为0,1,2,所以点B1的坐标是(0,1,2)