
全程设计 8.5.2 直线与平面平行
8.5.2 直线与平面平行

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破
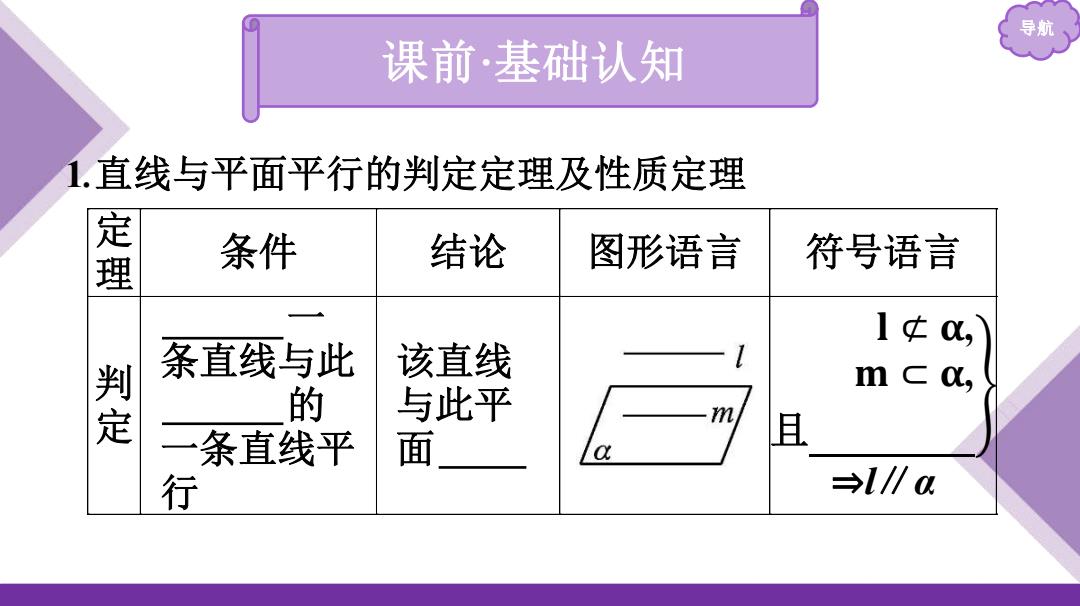
导航 课前·基础认知 1直线与平面平行的判定定理及性质定理 蜜 条件 结论 图形语言 符号语言 1中0, 条直线与此 该直线 m c a, 定 的 与此平 m 条直线平 面 且 行 →l/∥a
导航 课前·基础认知 1.直线与平面平行的判定定理及性质定理 定 理 条件 结论 图形语言 符号语言 判 定 平面外 一 条直线与此 平面内 的 一条直线平 行 该直线 与此平 面 平行 𝐥 ⊄ 𝛂, 𝐦 ⊂ 𝛂, 且 𝐥 ∥ 𝐦 ⇒l∥α
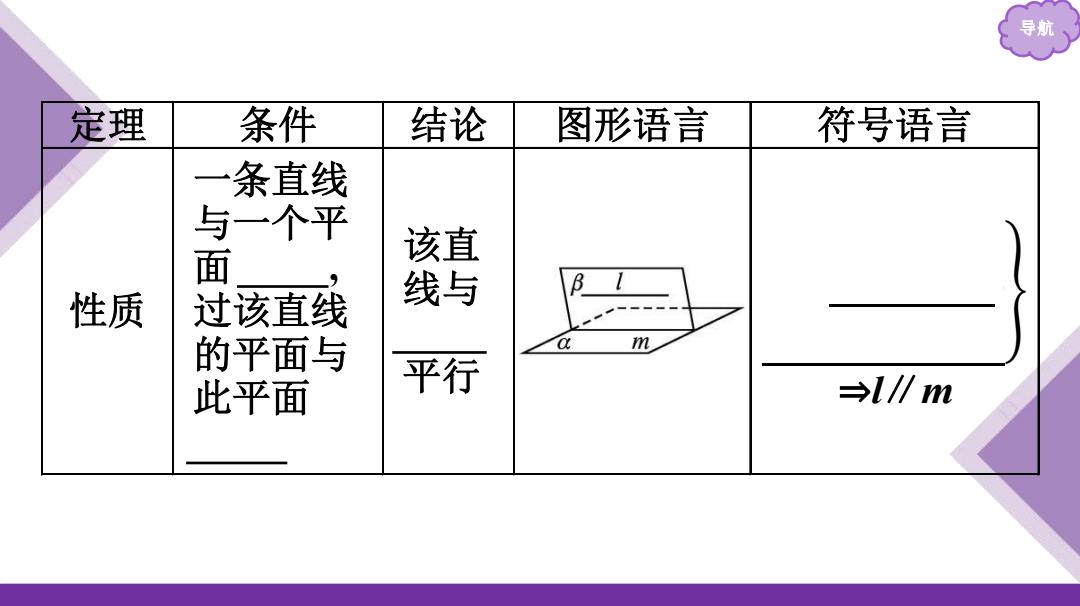
导航 定理 条件 结论 图形语言 符号语言 一条直线 与一个平 面 该直 性质 过该直线 线与 的平面与 a m 此平面 平行 →l/∥m
导航 定理 条件 结论 图形语言 符号语言 性质 一条直线 与一个平 面 平行 , 过该直线 的平面与 此平面 相交 该直 线与 交线 平行 𝐥 ∥ 𝛂, 𝐥 ⊂ 𝛃 , 𝛂⋂𝛃 = 𝐦 ⇒l∥m

微思考 (1)若一条直线平行于一个平面内的一条直线,则 这条直线和这个平面平行,对吗? 提示:根据直线与平面平行的判定定理可知该结论错误,该 直线可能在平面内. (2)若直线l∥平面a,则平行于平面a内的所有直线吗? 提示:不是 3)若a∥a,过a与a相交的平面有多少个?这些平面与a的交 线与直线有什么关系? 提示:若a∥a,则过a且与a相交的平面有无数个.这些平面 与a的交线与直线相互平行
导航 微思考 (1)若一条直线平行于一个平面内的一条直线,则 这条直线和这个平面平行,对吗? 提示:根据直线与平面平行的判定定理可知该结论错误,该 直线可能在平面内. (2)若直线l∥平面α,则l平行于平面α内的所有直线吗? 提示:不是. (3)若a∥α,过a与α相交的平面有多少个?这些平面与α的交 线与直线a有什么关系? 提示:若a∥α,则过a且与α相交的平面有无数个.这些平面 与α的交线与直线a相互平行

导航 课堂·重难突破 直线与平面平行的判定定理的应用 典例剖析 1如图,在斜三棱柱ABC-A1B1C1中,CA=CB,D,E分别是 AB,B,C的中点. Av 求证:DE∥平面ACCA1, B B
导航 课堂·重难突破 一 直线与平面平行的判定定理的应用 典例剖析 1.如图,在斜三棱柱ABC-A1B1C1中,CA=CB,D,E分别是 AB,B1C的中点. 求证:DE∥平面ACC1A1

导航 证明:如图,连接BC1,AC· 由题意可知,四边形BCCB是平行四边形, A 因为E是BC的中点, 所以E也是BC,的中点, 又D是AB的中点,所以DE∥AC· 又DE女平面ACCA1,ACC平面ACC1A1, 所以DE∥平面ACCA·
导航 证明:如图,连接BC1 ,AC1 . 由题意可知,四边形BCC1B1是平行四边形, 因为E是B1C的中点, 所以E也是BC1的中点. 又D是AB的中点,所以DE∥AC1 . 又DE⊄平面ACC1A1 ,AC1⊂平面ACC1A1 , 所以DE∥平面ACC1A1

导航 规律总结 1.利用直线与平面平行的判定定理证明线面平行,关键是在 平面内寻找一条与已知直线平行的直线 2.证明:线线平行常用三角形中位线定理、平行四边形的 性质、基本事实4等
导航 规律总结 1.利用直线与平面平行的判定定理证明线面平行,关键是在 平面内寻找一条与已知直线平行的直线. 2.证明:线线平行常用三角形中位线定理、平行四边形的 性质、基本事实4等
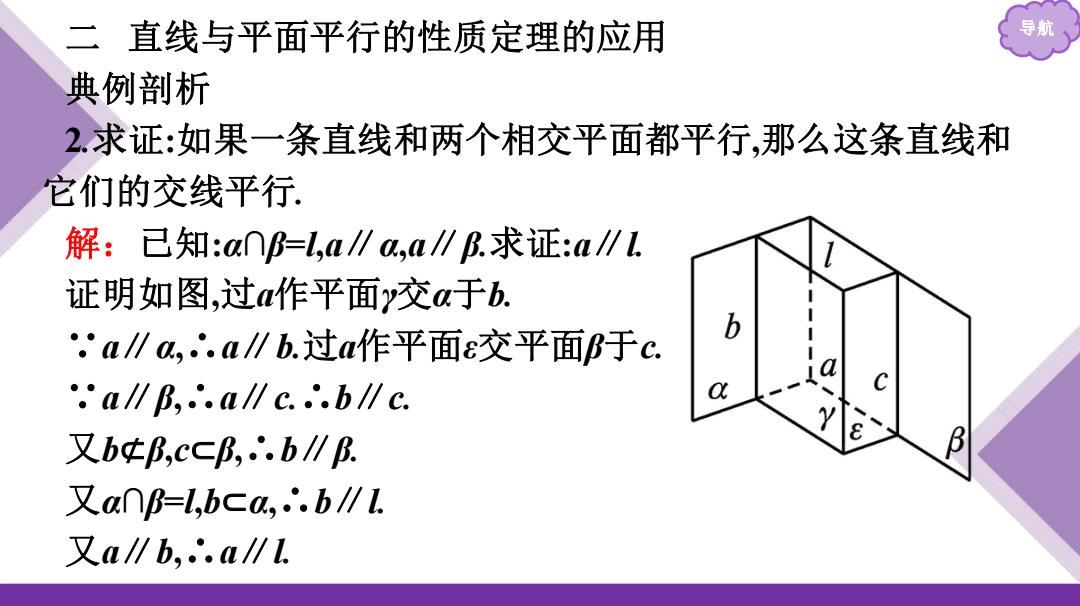
二直线与平面平行的性质定理的应用 典例剖析 2.求证:如果一条直线和两个相交平面都平行,那么这条直线和 它们的交线平行 解:已知:a∩f=L,a∥a,a∥B.求证:a∥1 证明如图,过a作平面y交a于b. b .a∥a,∴.a∥b.过a作平面交平面f于c .a∥B,.a∥c∴.b∥c 又btp,cCf,∴.b∥B. B 又anf=l,bca,∴.b∥l 又a∥b,∴.a∥1
二 直线与平面平行的性质定理的应用 导航 典例剖析 2.求证:如果一条直线和两个相交平面都平行,那么这条直线和 它们的交线平行. 解:已知:α∩β=l,a∥α,a∥β.求证:a∥l. 证明如图,过a作平面γ交α于b. ∵a∥α,∴a∥b.过a作平面ε交平面β于c. ∵a∥β,∴a∥c.∴b∥c. 又b⊄β,c⊂β,∴b∥β. 又α∩β=l,b⊂α,∴b∥l. 又a∥b,∴a∥l

导航 规律总结运用线面平行的性质定理时,应先确定线面平行, 再寻找过已知直线的平面与这个平面的交线,最后确定线线 平行
导航 规律总结 运用线面平行的性质定理时,应先确定线面平行, 再寻找过已知直线的平面与这个平面的交线,最后确定线线 平行