
全程设计 第1课时棱柱、棱锥、 棱台的结构特征
第1课时 棱柱、棱锥、棱台的结构特征

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 1空间几何体 类别 多面体 旋转体 一条平面曲线(包括直线) 一 般地,由若干个平 绕它所在平面内的一条定 定义 面多边形围成的几何 直线旋转所形成的曲面叫 体叫做多面体 做旋转面,封闭的旋转面 围成的几何体叫做旋转体
导航 课前 ·基础认知 1 .空间几何体 类别 多面体 旋转体 定义 一般地,由若干个平 面多边形围成的几何 体叫做多面体 一条平面曲线(包括直线) 绕它所在平面内的一条定 直线旋转所形成的曲面叫 做旋转面,封闭的旋转面 围成的几何体叫做旋转体
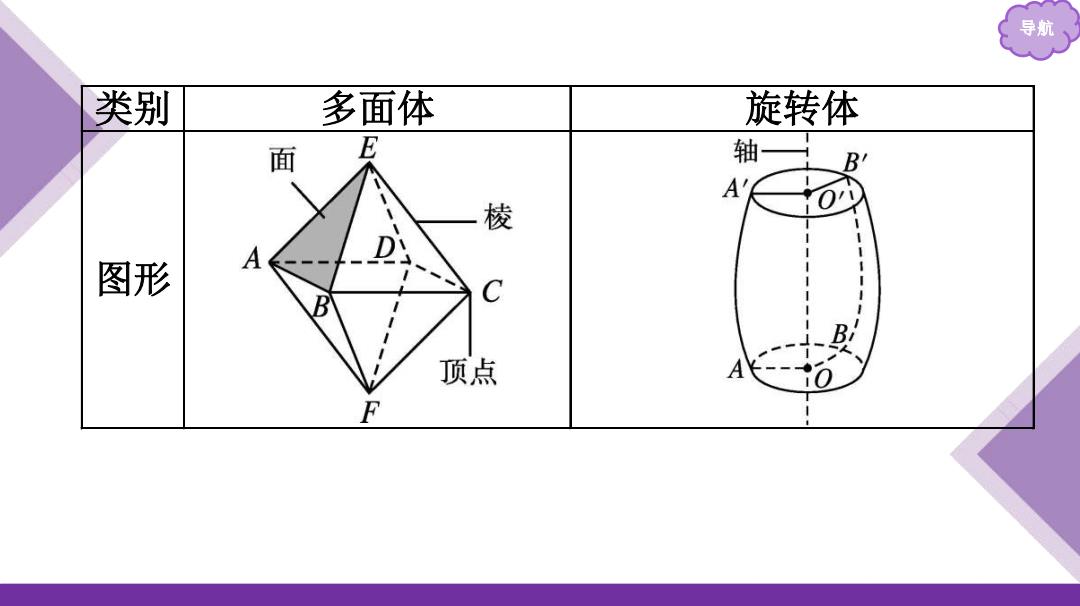
导航 类别 多面体 旋转体 面 E 轴 B A 棱 10 图形 A B 顶点 F
导航 类别 多面体 旋转体 图形
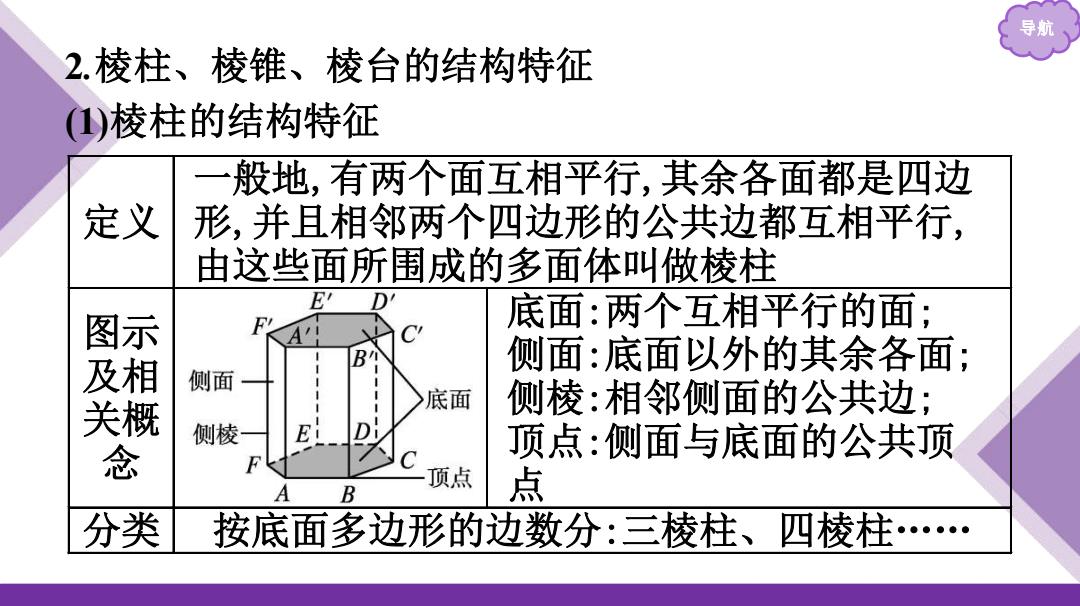
导期 2.棱柱、棱锥、棱台的结构特征 )棱柱的结构特征 一 般地,有两个面互相平行,其余各面都是四边 定义 形,并且相邻两个四边形的公共边都互相平行, 由这些面所围成的多面体叫做棱柱 恩 底面:两个互相平行的面; 相 侧面:底面以外的其余各面; 侧面 底面 侧棱:相邻侧面的公共边; 侧棱 E 念 顶点:侧面与底面的公共顶 F 顶点 B 点 分类 按底面多边形的边数分:三棱柱、四棱柱
导航 2 .棱柱、棱锥、棱台的结构特征 (1)棱柱的结构特征 定义 一般地,有两个面互相平行,其余各面都是四边 形,并且相邻两个四边形的公共边都互相平行, 由这些面所围成的多面体叫做棱柱 图示 及相 关概 念 底面:两个互相平行的面; 侧面:底面以外的其余各面; 侧棱:相邻侧面的公共边; 顶点:侧面与底面的公共顶 点 分类 按底面多边形的边数分:三棱柱、四棱柱……

导 微思考1棱柱的侧面一定是平行四边形吗? 是示:根据棱柱的概念可知,棱柱侧面一定是平行四边形 2)棱柱的分类 直棱柱:侧棱 于底面的棱柱 斜棱柱:侧棱不垂直于底面的棱柱 正棱柱:底面是 的直棱柱 平行六面体:底面是 的四棱柱
导航 微思考1 棱柱的侧面一定是平行四边形吗? 提示:根据棱柱的概念可知,棱柱侧面一定是平行四边形. (2)棱柱的分类 直棱柱:侧棱 垂直 于底面的棱柱. 斜棱柱:侧棱不垂直于底面的棱柱. 正棱柱:底面是 正多边形 的直棱柱. 平行六面体:底面是 平行四边形 的四棱柱
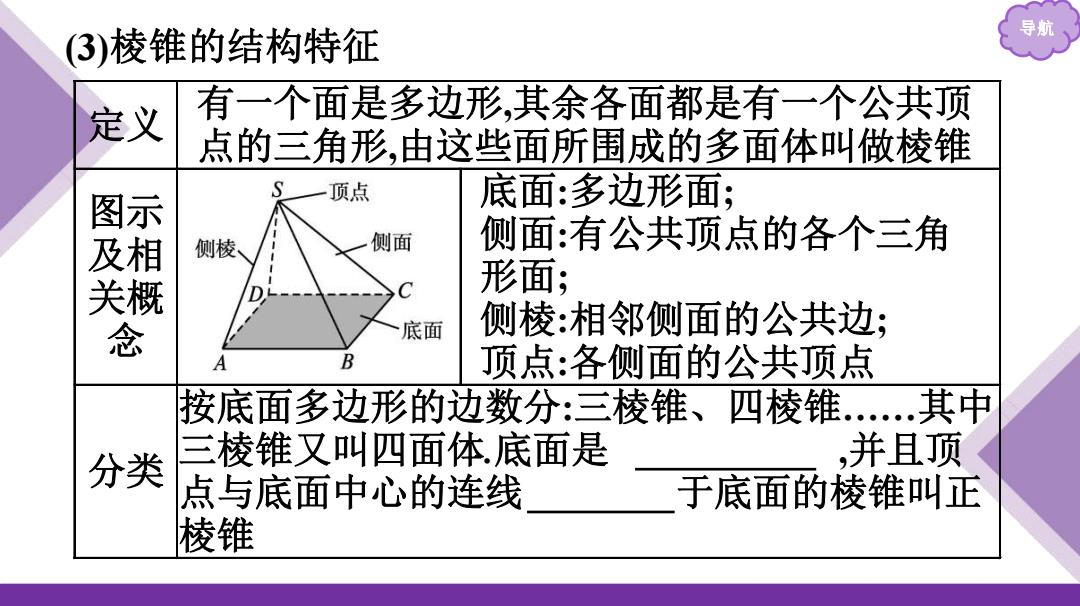
(3)棱锥的结构特征 导财 定义 有一个面是多边形,其余各面都是有一个公共顶 点的三角形,由这些面所围成的多面体叫做棱锥 顶点 底面:多边形面; 图及关 侧面:有公共顶点的各个三角 相概 侧棱 侧面 形面; 底面 侧棱:相邻侧面的公共边; B 顶点:各侧面的公共顶点 按底面多边形的边数分:三棱锥、四棱锥..其中 分类 三棱锥又叫四面体.底面是 ,并且顶 点与底面中心的连线 于底面的棱锥叫正 棱锥
导航 (3)棱锥的结构特征 定义 有一个面是多边形,其余各面都是有一个公共顶 点的三角形,由这些面所围成的多面体叫做棱锥 图示 及相 关概念 底面:多边形面; 侧面:有公共顶点的各个三角 形面; 侧棱:相邻侧面的公共边; 顶点:各侧面的公共顶点 分类 按底面多边形的边数分:三棱锥、四棱锥……其中 三棱锥又叫四面体.底面是 正多边形 ,并且顶 点与底面中心的连线 垂直 于底面的棱锥叫正 棱锥

导航 微思考2有一个面是多边形,其余各面是三角形的几何体 一定是棱锥吗? 提示:不一定.因为“其余各面都是三角形”并不等价于“其 余各面都是有一个公共顶点的三角形
导航 微思考2 有一个面是多边形,其余各面是三角形的几何体 一定是棱锥吗? 提示:不一定.因为“其余各面都是三角形”并不等价于“其 余各面都是有一个公共顶点的三角形”

导航 (4)棱台的结构特征 定义 用一个平行于棱锥底面的平面去截棱锥,底面和 截面之间的部分叫做棱台 上底面:原棱锥的截面; 雨 下底面:原棱锥的底面; 侧面:除上下底面以外的面; 关 上底面 侧面 侧棱 侧棱:相邻侧面的公共边; 顶点 下底面 项点:侧面与上下)底面的公 共顶点 分类 由对应的棱锥截得,如三棱台、四棱台
导航 (4)棱台的结构特征 定义 用一个平行于棱锥底面的平面去截棱锥,底面和 截面之间的部分叫做棱台 图示 及相 关概念 上底面:原棱锥的截面; 下底面:原棱锥的底面; 侧面:除上下底面以外的面; 侧棱:相邻侧面的公共边; 顶点:侧面与上(下)底面的公 共顶点 分类 由对应的棱锥截得,如三棱台、四棱台……

导航 微思考3棱台的上下底面互相平行,各侧棱延长线一定相 交于一点吗? 提示:根据棱台的定义可知其侧棱延长线一定交于一点:
导航 微思考3 棱台的上下底面互相平行,各侧棱延长线一定相 交于一点吗? 提示:根据棱台的定义可知其侧棱延长线一定交于一点