
全程设计 第1课时 向量数量积的概念
第1课时 向量数量积的概念

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破
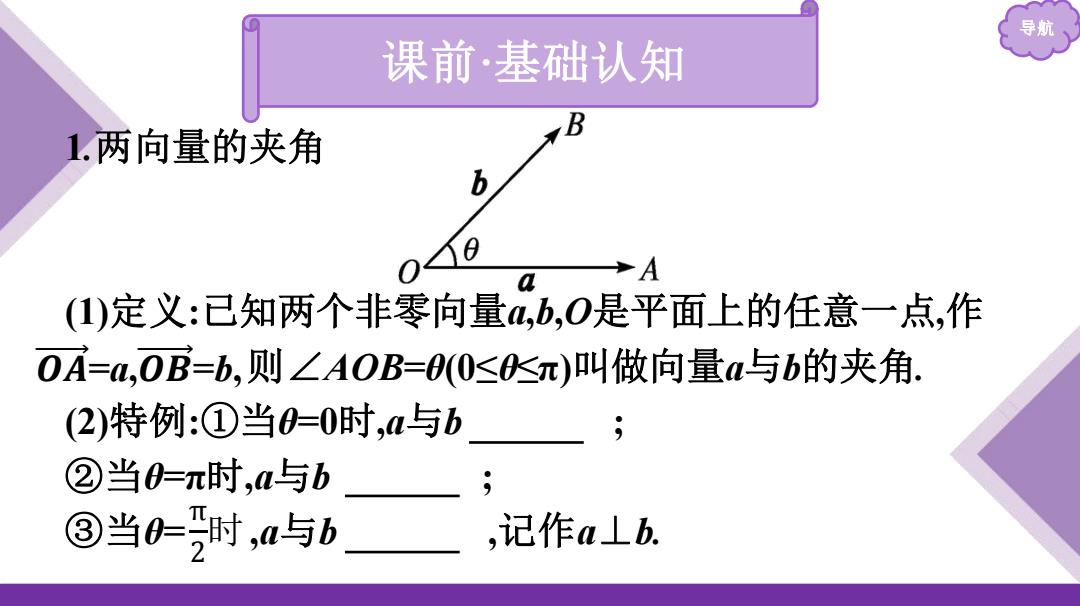
导航 课前·基础认知 1.两向量的夹角 A (1)定义:已知两个非零向量4,b,O是平面上的任意一点,作 OA=a,OB=b,则∠AOB=00≤sπ)叫做向量a与b的夹角. (2)特例:①当0=0时,a与b ②当0=π时,a与b ③当时,a与b,记作m1b
导航 课前·基础认知 1.两向量的夹角 (1)定义:已知两个非零向量a,b,O是平面上的任意一点,作 则∠AOB=θ(0≤θ≤π)叫做向量a与b的夹角. (2)特例:①当θ=0时,a与b 同向 ; ②当θ=π时,a与b 反向 ; ③当θ= ,a与b 垂直 ,记作a⊥b. 𝑶 𝑨 =a,𝑶 𝑩 =b, π 2 时

导航 微提醒 要注意夹角0的范围0∈[0,, 当cos0时,0∈[0,): 当c0s00时,0∈(经,,当c0s0时,0究
导航 微提醒 要注意夹角 θ 的范围 θ∈[0,π], 当 cos θ>0 时,θ∈ 𝟎, 𝛑 𝟐 ; 当 cos θ<0 时,θ∈ 𝛑 𝟐 ,𝛑 ,当 cos θ=0 时,θ=𝛑 𝟐

2.向量数量积的定义 已知两个非零向量a与b,它们的夹角为0,我们把数量bcos 叫做向量a与b的数量积(或内积),记作b, 即ab=alblcos0. 规定:零向量与任一向量的数量积为 微思考向量数量积的运算结果与线性运算的结果有什么 不同? 提示:两个向量数量积的运算结果是一个数量,向量线性运 算的结果是一个向量
导航 2.向量数量积的定义 已知两个非零向量a与b,它们的夹角为θ,我们把数量|a||b|cos θ叫做向量a与b的数量积(或内积),记作a·b, 即a·b=|a||b|cos θ. 规定:零向量与任一向量的数量积为 0 . 微思考 向量数量积的运算结果与线性运算的结果有什么 不同? 提示:两个向量数量积的运算结果是一个数量,向量线性运 算的结果是一个向量

导航 3.投影向量 B a BD 设a,b是两个非零向量,AB=a,CD=b,过AB的起点A和终点B, 分别作CD所在直线的垂线,垂足分别为A1,B1,得到A1B1,我们 称这种变换为向量α向向量b ,A1B1,叫做向量在向 量b上的
导航 3.投影向量 设a,b是两个非零向量, 过 的起点A和终点B, 分别作 所在直线的垂线,垂足分别为A1 ,B1 ,得到 我们 称这种变换为向量a向向量b 投影 , 叫做向量a在向 量b上的 投影向量 . 𝑨 𝑩 =a,𝑪 𝑫 =b, 𝑨 𝑩 𝑪 𝑫 𝑨𝟏 𝑩𝟏 , 𝑨𝟏 𝑩𝟏

导加 4.向量数量积的性质 设a,b是非零向量,它们的夹角是0,e是与b方向相同的单位向 量,则 (1)a-e=e-a=acos 0. (2)a⊥b台 =0. (3)当a与b同向时,ab= 当a与b反向时,b= 特别地,a=lal或a=。 (4)川a'b1 allbl
导航 4.向量数量积的性质 设a,b是非零向量,它们的夹角是θ,e是与b方向相同的单位向 量,则 (1)a·e=e·a=|a|cos θ. (2)a⊥b⇔ a·b =0. (3)当a与b同向时,a·b= |a||b| ; 当a与b反向时,a·b= -|a||b| . 特别地,a·a=|a|2或|a|= . (4)|a·b| ≤ |a||b|. 𝑎·𝑎

导航 课堂·重难突破 一、向量的夹角问题 典例剖析 1.己知@=b=2,且a与b的夹角为60°,则a叶b与a的夹角是多 少?a-b与a的夹角又是多少?
导航 课堂·重难突破 一、向量的夹角问题 典例剖析 1.已知|a|=|b|=2,且a与b的夹角为60° ,则a+b与a的夹角是多 少?a-b与a的夹角又是多少?

导 解:如图所示,作0A=a,0B=b,且∠AOB=60°. 以OA,OB为邻边作平行四边形OACB, B 则0C=a+b,BA=a-b. b 因为la=bl=2, 所以平行四边形OACB是菱形, a 又∠AOB=60°,所以0C与0A的夹角为30°, BA与0A的夹角为60°. 即a+b与a的夹角是30°,a-b与a的夹角是60°
导航 解:如图所示,作𝑶 𝑨 =a,𝑶 𝑩 =b,且∠AOB=60°. 以 OA,OB 为邻边作平行四边形 OACB, 则𝑶 𝑪 =a+b,𝑩 𝑨 =a-b. 因为|a|=|b|=2, 所以平行四边形 OACB 是菱形, 又∠AOB=60°,所以𝑶 𝑪 与𝑶 𝑨 的夹角为 30°, 𝑩 𝑨 与𝑶 𝑨 的夹角为 60°. 即 a+b 与 a 的夹角是 30°,a-b 与 a 的夹角是 60°

导航 二、数量积的定义及几何意义 典例剖析 2已知lb-品,a与b的夹角=120° 2 1)求ab; (2)求在b上的投影向量
导航 二、数量积的定义及几何意义 典例剖析 (1)求a·b; (2)求a在b上的投影向量. 2.已知|a|=𝟑 𝟓 ,|b|= 𝟐 𝟏𝟏 ,a 与 b 的夹角 θ=120°