
全程设计 第四章 指数数与对数数 4.4对数函数 第1课时 对数函数的概念与图象
第四章 指数函数与对数函数 4.4 对数函数 第1课时 对数函数的概念与图象

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 1.对数函数的概念 一 般地,函数 叫做对数函数,其中 是自变量,定义域是 微判断()函数log2是对数函数(×)》 (2)函数y=2l0g3x是对数函数.(× ) (3)函数y=l0g3c+1)的定义域是(0,+o).(×)
导航 课前·基础认知 1.对数函数的概念 一般地,函数 y=logax(a>0,且a≠1) 叫做对数函数,其中 x 是自变量,定义域是 (0,+∞) . 微判断 (1)函数y=logx 是对数函数.( ) (2)函数y=2log3x是对数函数.( ) (3)函数y=log3 (x+1)的定义域是(0,+∞).( ) 𝟏 𝟐 × × ×
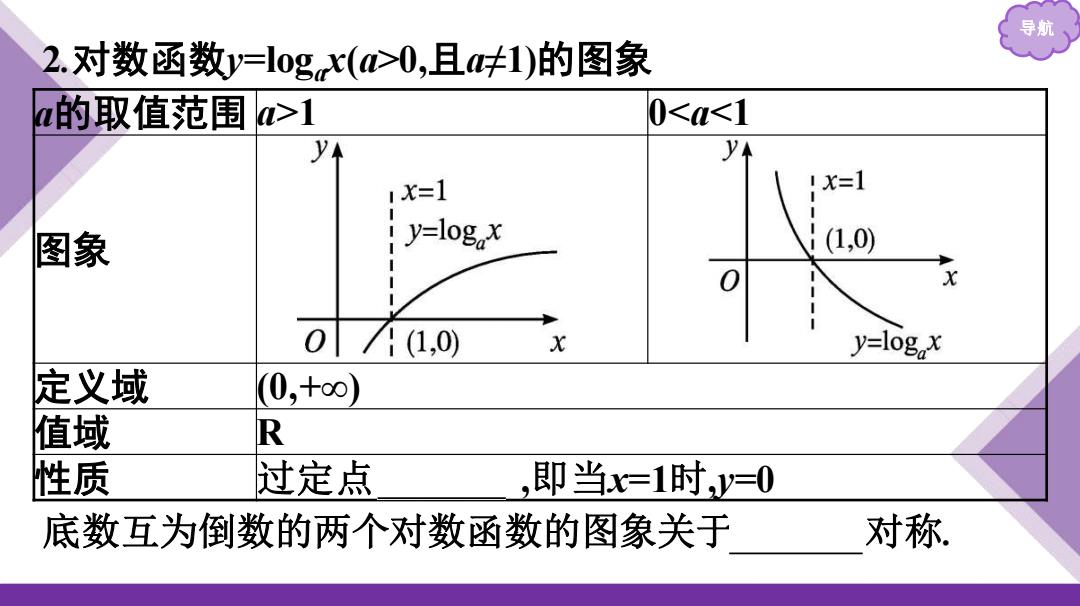
导航 2.对数函数y=log(心0,且a呋1)的图象 的取值范围>1 0<a<1 y y 1x=1 !x=1 图象 iy=logx (1,0) 071(1,0) x y=log x 定义域 (0,+o∞) 值域 R 性质 过定点 ,即当=1时,y=0 底数互为倒数的两个对数函数的图象关于 对称
导航 2.对数函数y=logax(a>0,且a≠1)的图象 a的取值范围 a>1 0<a<1 图象 定义域 (0,+∞) 值域 R 性质 过定点 (1,0) ,即当x=1时,y=0 底数互为倒数的两个对数函数的图象关于 x轴 对称

微训练(1)对数函数y=logx与y=logx的图象如图,则( A.a0 C.01 D.00,且呋1)的图象恒过定点
导航 微训练 (1)对数函数y=logax与y=logbx的图象如图,则( ) A.a0 C.01 D.00,且a≠1)的图象恒过定点

导航 答案:1)C(2)B (3)(4,3) 10g1(4x-3)≥0, 3-4 0, x> , 故x∈(1], 故选B. (3)当x-3=1,即x=4时y=l0gk-3)+3=0+3=3, 所以函数y=l0gc-3)+3的图象恒过定点(4,3)
导航 答案:(1)C (2)B (3)(4,3) 解析:(2)由题意可得 𝐥𝐨𝐠𝟏 𝟐 (𝟒𝒙-𝟑) ≥ 𝟎, 𝟒𝒙-𝟑 > 𝟎, 解得 𝟑 𝟒 𝟑 𝟒 , 故 x∈ 𝟑 𝟒 ,1 . 故选B. (3)当x-3=1,即x=4时,y=loga (x-3)+3=0+3=3, 所以函数y=loga (x-3)+3的图象恒过定点(4,3)

导航 课堂·重难突破 对数函数的概念及应用 典例剖析 1.(1)下列函数中,是对数函数的有( ①=log2;②y=logx(a∈R);③y=logg;④y=lnx;⑤y=log.(x+2); ⑥y=2log4x;⑦y=log2(x+1), A.1个 B.2个 C.3个 D.4个 (2)若对数函数fx)的图象过点(4,-2),则f8)=
导航 课堂·重难突破 一 对数函数的概念及应用 典例剖析 1.(1)下列函数中,是对数函数的有( ) ①y=logx2;②y=logax(a∈R);③y=log8x;④y=ln x;⑤y=logx (x+2); ⑥y=2log4x;⑦y=log2 (x+1). A.1个 B.2个 C.3个 D.4个 (2)若对数函数f(x)的图象过点(4,-2),则f(8)=

导航 答案:(1)B(2)3 解析:1)①中自变量在底数位置上, ①不是对数函数; .②中底数a∈R不能保证>0,且呋1, ②不是对数函数; .⑤⑦的真数分别为x+2,x+1, .⑤⑦不是对数函数; .⑥中对数符号前面的系数为2, .⑥不是对数函数;只有③④符合对数函数的定义
导航 答案:(1)B (2)-3 解析:(1)∵①中自变量在底数位置上, ∴①不是对数函数; ∵②中底数a∈R不能保证a>0,且a≠1, ∴②不是对数函数; ∵⑤⑦的真数分别为x+2,x+1, ∴⑤⑦不是对数函数; ∵⑥中对数符号前面的系数为2, ∴⑥不是对数函数;只有③④符合对数函数的定义

导航 (2)由题意设fx)=l0gx(a>0,且呋1),'fx)的图象过点(4,-2), 'f4)=l0g4=-2, ∴2=4,得2 ∴x)=log1x,于是8)=log18=3
导航 (2)由题意设f(x)=logax(a>0,且a≠1),∵f(x)的图象过点(4,-2), ∴f(4)=loga4=-2, ∴a -2 =4,得 a= 𝟏 𝟐 , ∴f(x)=lo𝐠𝟏 𝟐 x,于是 f(8)=lo𝐠𝟏 𝟐 8=-3
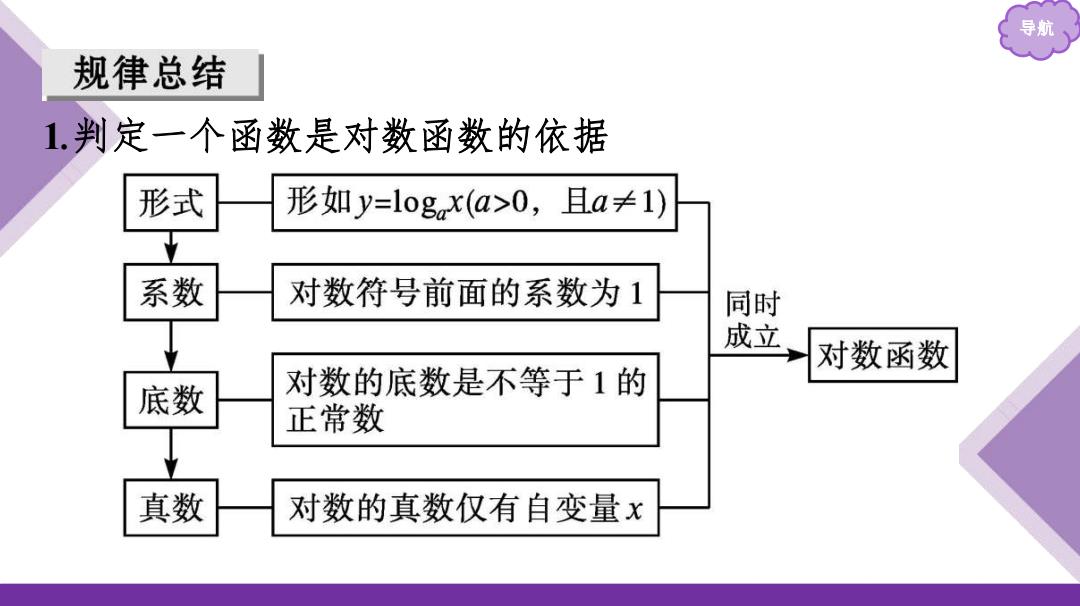
导航 规律总结 1.判定一个函数是对数函数的依据 形式 形如y=logx(a>0,且a≠1) 系数 对数符号前面的系数为1 同时 成立 对数函数 底数 对数的底数是不等于1的 正常数 真数 对数的真数仅有自变量x
导航 1.判定一个函数是对数函数的依据