
全程设计 第五章 三角丞数 5.5三角恒等变换 5.5.1 两角和与差的正弦、余弦和正物公式 第2课时 两角和与差的正弦、余弦、正切公式
第五章 三角函数 5.5 三角恒等变换 5.5.1 两角和与差的正弦、余弦和正切公式 第2课时 两角和与差的正弦、余弦、正切公式

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 1.两角和的余弦公式 cos(a+B)= ,简记为 2.两角和与差的正弦公式 sin(a+B)- ,简记为 sin(a-B)= ,简记为
导航 课前·基础认知 1.两角和的余弦公式 cos(α+β)= cos αcos β-sin αsin β ,简记为 C(α+β) . 2.两角和与差的正弦公式 sin(α+β)= sin αcos β+cos αsin β ,简记为 S(α+β) . sin(α-β)= sin αcos β-cos αsin β ,简记为 S(α-β)

导航、 微点拨1(1)公式的结构特征: 同角的余弦、正弦 cos(a+B)=cos acosB-sinasinB 同角α的余弦、正弦 同角β的余弦、正弦 sin(a±B)=-sin acosB±cos asinB 同角α的正弦、余弦
导航 微点拨1 (1)公式的结构特征:

导期 (2)两角和的余弦公式的记忆要诀: 两角和的余弦值等于两角的余弦值乘积减去两角的正弦值 乘积. 记忆时要与两角和与差的正弦公式区别开来,两角和与差的 正弦公式的右端的两部分为异名三角函数之积,连接符号与 左端的连接符号相同。 (3)使用范围:,B为任意角,可以是一个角,也可以是角的组合:
导航 (2)两角和的余弦公式的记忆要诀: 两角和的余弦值等于两角的余弦值乘积减去两角的正弦值 乘积. 记忆时要与两角和与差的正弦公式区别开来,两角和与差的 正弦公式的右端的两部分为异名三角函数之积,连接符号与 左端的连接符号相同. (3)使用范围:α,β为任意角,可以是一个角,也可以是角的组合

导航 微训练1(1)sin131°sin19°+cos19°sin41°=( 2 2 D (2)sin345°=() V6-V2 B.4 CV6+V2 6+V2 D. 4 4
导航 微训练1 (1)sin 131°sin 19°+cos 19°sin 41° =( ) A. 𝟏 𝟐 B.- 𝟏 𝟐 C. 𝟑 𝟐 D.- 𝟑 𝟐 (2)sin 345°=( ) A. 𝟐- 𝟔 𝟒 B. 𝟔- 𝟐 𝟒 C.- 𝟔+ 𝟐 𝟒 D. 𝟔+ 𝟐 𝟒

导航 答案:(1)C(2)A 解析:(1)sin131°sin19°+cos19°sin41°=sin(90°+41)sin 19°+c0s19°sin41° =c0s41°sin19°+c0s19°sin41°=sin(19°+41) =sin60°=3 故选C (2)sin345°=sin(360°-15)=-sin15°=-sin(45°-30) V2-V6 =-sin45°c0s30°+c0s45°sin30°= ·4 故选A
导航 答案:(1)C (2)A 解析:(1)sin 131°sin 19°+cos 19°sin 41° =sin(90°+41°)sin 19°+cos 19°sin 41° =cos 41°sin 19°+cos 19°sin 41° =sin(19°+41°) =sin 60° = . 故选C. (2)sin 345° =sin(360°-15°)=-sin 15° =-sin(45°-30°) =-sin 45° cos 30°+cos 45°sin 30° = . 故选A. 𝟑 𝟐 𝟐- 𝟔 𝟒

导航 3.两角和与差的正切公式 tan(a+) tana+tang 1-tanatanB ,简记为 tan(c-)1tanctan tana-tanβ 简记为 公式Sa+Ca+,Ta+给出了任意角a,B的三角函数值与其和 角α+B的三角函数值之间的关系,为方便起见,我们把这三个 公式都叫做 ,类似地,Sa-,Ca-,T(a-都叫做
导航 3.两角和与差的正切公式 tan(α+β)= 𝐭𝐚𝐧𝜶+𝐭𝐚𝐧𝜷 𝟏-𝐭𝐚𝐧𝜶𝐭𝐚𝐧𝜷 ,简记为 T(α+β) . tan(α-β)= 𝐭𝐚𝐧𝜶-𝐭𝐚𝐧𝜷 𝟏+𝐭𝐚𝐧𝜶𝐭𝐚𝐧𝜷 ,简记为 T(α-β) . 公式S(α+β) ,C(α+β) ,T(α+β)给出了任意角α,β的三角函数值与其和 角α+β的三角函数值之间的关系,为方便起见,我们把这三个 公式都叫做 和角公式 ,类似地,S(α-β) ,C(α-β) ,T(α-β)都叫做 差角公式
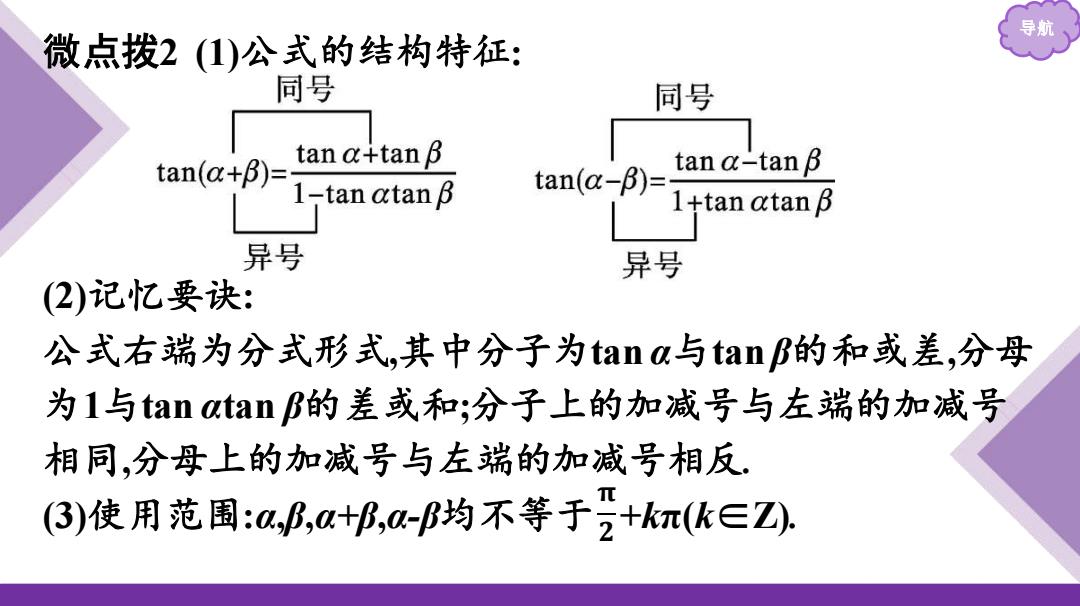
导航 微点拨2(1)公式的结构特征: 同号 同号 tan(a+β)= tan a+tan B tan a-tan B 1-tan atan B 1+tan atan B 异号 异号 2)记忆要诀: 公式右端为分式形式,其中分子为ana与tanB的和或差,分母 为1与tan atan B的差或和;分子上的加减号与左端的加减号 相同,分母上的加减号与左端的加减号相反. (3)使用范围:a,B,a+f,a-B均不等于,+kπ(k∈Z)
导航 微点拨2 (1)公式的结构特征: (2)记忆要诀: 公式右端为分式形式,其中分子为tan α与tan β的和或差,分母 为1与tan αtan β的差或和;分子上的加减号与左端的加减号 相同,分母上的加减号与左端的加减号相反. (3)使用范围:α,β,α+β,α-β均不等于 +kπ(k∈Z). 𝛑 𝟐

导月 微判断(1)不存在角a,P,使得cos(a+)=cos acos+sin asin B. (X) (2)对于任意角a,f,都有sin(a+=sin acos B-+cos asin B.(V) (d对于任意角ag总有an(a+价(×) 解析:(1)如a=f=0,cos(a+)=cos0=1,cos acos+sin asin=1. (2)由两角和的正弦公式知结论正确. (3)公式成立需a,B,+B均不等于km+2,k∈Z
导航 微判断(1)不存在角α,β,使得cos(α+β)=cos αcos β+sin αsin β. ( ) (2)对于任意角α,β,都有sin(α+β)=sin αcos β+cos αsin β.( ) (3)对于任意角α,β,总有tan(α+β)= 𝐭𝐚𝐧𝜶+𝐭𝐚𝐧𝜷 𝟏−𝐭𝐚𝐧𝜶𝐭𝐚𝐧𝜷.( ) 解析:(1)如α=β=0,cos(α+β)=cos 0=1,cos αcos β+sin αsin β=1. (2)由两角和的正弦公式知结论正确. (3)公式成立需α,β,α+β均不等于kπ+ ,k∈Z. 𝛑 𝟐 × ×