
全程设计 10.1.1 有限样体空间与随机事件
10.1.1 有限样本空间与随机事件

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导月 课前·基础认知 1.随机试验的概念和特点 随机试验:我们把对 的实现和对它的观察称为 随机试验,简称试验,常用字母E表示我们感兴趣的是具有以 下特点的随机试验: (1)试验可以在相同条件下 进行; (2)试验的所有可能结果是 的,并且不止一个; 3)每次试验总是恰好出现这些可能结果中的一个,但事先不 能确定出现哪一个结果
导航 课前·基础认知 1.随机试验的概念和特点 随机试验:我们把对 随机现象 的实现和对它的观察称为 随机试验,简称试验,常用字母E表示.我们感兴趣的是具有以 下特点的随机试验: (1)试验可以在相同条件下 重复 进行; (2)试验的所有可能结果是 明确可知 的,并且不止一个; (3)每次试验总是恰好出现这些可能结果中的一个,但事先不 能确定出现哪一个结果
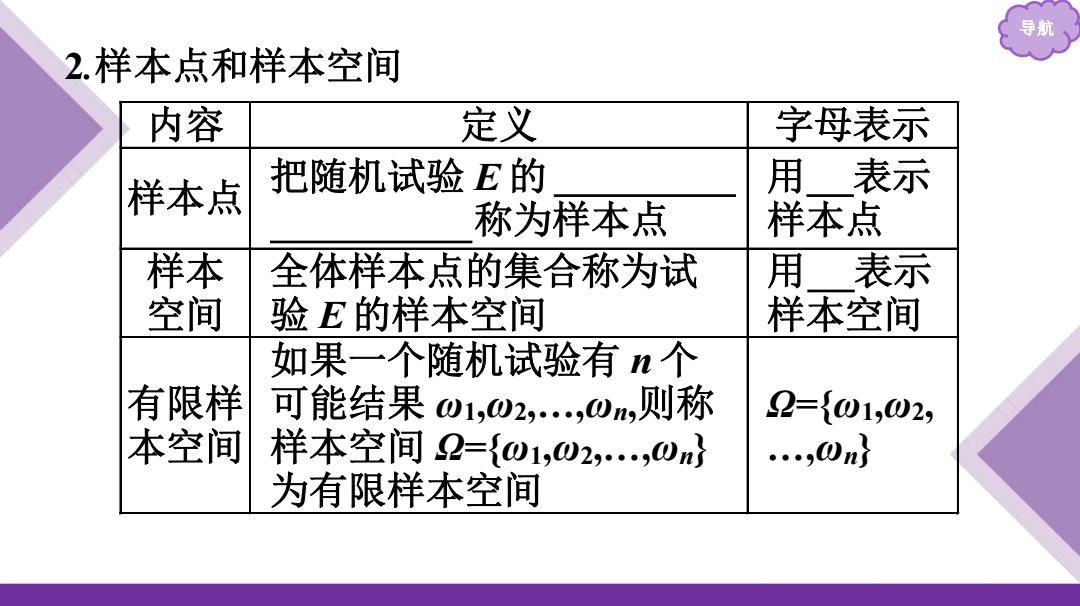
导航 2.样本点和样本空间 内容 定义 字母表示 样本点 把随机试验E的 用 表示 称为样本点 样本点 样本 全体样本点的集合称为试 用表示 空间 验E的样本空间 样本空间 如果一个随机试验有n个 有限样 可能结果01,02,,0,则称 2={01,02, 本空间 样本空间2={01,02,,0m} .…,0n} 为有限样本空间
导航 2 .样本点和样本空间 内容 定义 字母表示 样本点 把随机试验 E 的 每个可能 的基本结果 称为样本点 用 ω 表示 样本点 样本 空间 全体样本点的集合称为试 验 E 的样本空间 用 Ω 表示 样本空间 有限样 本空间 如果一个随机试验有 n 个 可能结果 ω1,ω 2,…, ω n,则称 样本空间 Ω={ ω1,ω 2,…, ω n} 为有限样本空间 Ω={ ω1,ω 2, …, ω n}

导航 微思考1(1)如何确定试验的样本空间? 提示:确定试验的样本空间就是写出试验的所有可能的结 果,并写成2={01,02,,0m}的形式。 (2)写试验的样本空间要注意些什么? 提示:要考虑周全,应想到试验的所有可能的结果,避免发 生遗漏和出现多余的结果
导航 微思考1 (1)如何确定试验的样本空间? 提示:确定试验的样本空间就是写出试验的所有可能的结 果,并写成Ω={ω1 ,ω2 ,…,ωn }的形式. (2)写试验的样本空间要注意些什么? 提示:要考虑周全,应想到试验的所有可能的结果,避免发 生遗漏和出现多余的结果

导航 3.三种事件的定义 将样本空间2的 称为随机事件,简 随机 称事件,并把只包含 样本点的事件 事件 称为基本事件.随机事件一般用大写字母 A,B,C,…表示在每次试验中,当且仅当A中 某个样本点出现时,称为事件A发生 必然 2作为自身的子集,包含了所有的样本点,在 事件 每次试验中总有 样本点发生,所以 2总会发生,我们称2为必然事件 不可能 空集⑦不包含任何样本点,在每次试验中都 事件 我们称②为不可能事件
导航 3 .三种事件的定义 随机 事件 将样本空间 Ω 的 子集 称为随机事件,简 称事件,并把只包含 一个 样本点的事件 称为基本事件.随机事件一般用大写字母 A,B,C,…表示.在每次试验中,当且仅当 A 中 某个样本点出现时,称为事件 A 发生 必然 事件 Ω 作为自身的子集,包含了所有的样本点,在 每次试验中总有 一个 样本点发生,所以 Ω 总会发生,我们称 Ω 为必然事件 不可能 事件 空集⌀不包含任何样本点,在每次试验中都 不会发生 ,我们称⌀为不可能事件

导航 微思考2观察随机试验时,其可能出现的结果的数量一定 是有限的吗? 提示:不一定,也可能是无限的.如在实数集中,任取一个实 数
导航 微思考2 观察随机试验时,其可能出现的结果的数量一定 是有限的吗? 提示:不一定,也可能是无限的.如在实数集中,任取一个实 数

导航 课堂·重难突破 写出随机试验的样本空间 典例剖析 1.写出下列各随机试验的样本空间: (1)从含有5件次品的100件产品中任取3件,记录其中的次品 数 (2)从装有大小和质地完全相同、分别标有,b,c,d的4个球的 袋中,任取1个球
导航 课堂·重难突破 一 写出随机试验的样本空间 典例剖析 1.写出下列各随机试验的样本空间: (1)从含有5件次品的100件产品中任取3件,记录其中的次品 数; (2)从装有大小和质地完全相同、分别标有a,b,c,d的4个球的 袋中,任取1个球

导航 解:(1)因为任取3件,次品数可能有0,1,2,3件,所以试验的样 本空间2={0,1,2,3}. (2)任取1个球,可能的基本结果为a,b,c,山,所以试验的样本空 间2={a,b,c
导航 解:(1)因为任取3件,次品数可能有0,1,2,3件,所以试验的样 本空间Ω={0,1,2,3}. (2)任取1个球,可能的基本结果为a,b,c,d,所以试验的样本空 间Ω={a,b,c,d}

导 规律总结不重不漏地列举试验的所有样本点的方法 (1)样本空间只与问题的背景有关,根据问题的背景明确试验 的每个可能的基本结果 (2)根据日常生活经验,按照一定的顺序列举出所有可能的结 果,用集合表示样本空间,也可以借助树状图、列表等方法帮 助我们列出试验的所有可能结果
导航 规律总结 不重不漏地列举试验的所有样本点的方法 (1)样本空间只与问题的背景有关,根据问题的背景明确试验 的每个可能的基本结果. (2)根据日常生活经验,按照一定的顺序列举出所有可能的结 果,用集合表示样本空间,也可以借助树状图、列表等方法帮 助我们列出试验的所有可能结果