
全程设计 6.2.1 向量的加法运算
6.2.1 向量的加法运算

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 1.向量加法的定义 ()定义:求 的运算,叫做向量的加法 (2)对于零向量与任意向量4,规定+_一=0+=一
导航 课前·基础认知 1.向量加法的定义 (1)定义:求 两个向量和 的运算,叫做向量的加法. (2)对于零向量与任意向量a,规定a+ 0 = 0+a= a
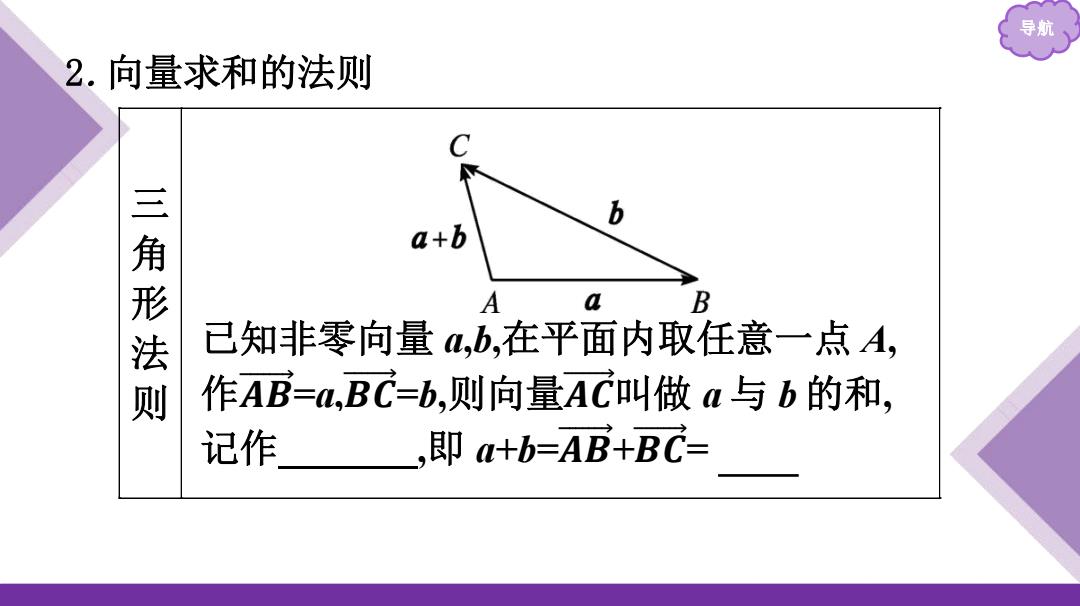
导航 2.向量求和的法测 b 三角形法则 a+b a B 已知非零向量a,b,在平面内取任意一点A, 作AB=,BC=b,则向量AC叫做a与b的和, 记作 ,即a+b=AB+BC=
导航 2 .向量求和的法则 三角形法则 已知非零向量 a,b,在平面内取任意一点 A, 作𝑨 𝑩 =a,𝑩 𝑪 =b,则向量𝑨 𝑪 叫做 a 与 b 的和, 记作 a+b ,即 a+b =𝑨 𝑩 + 𝑩 𝑪 = 𝑨 𝑪
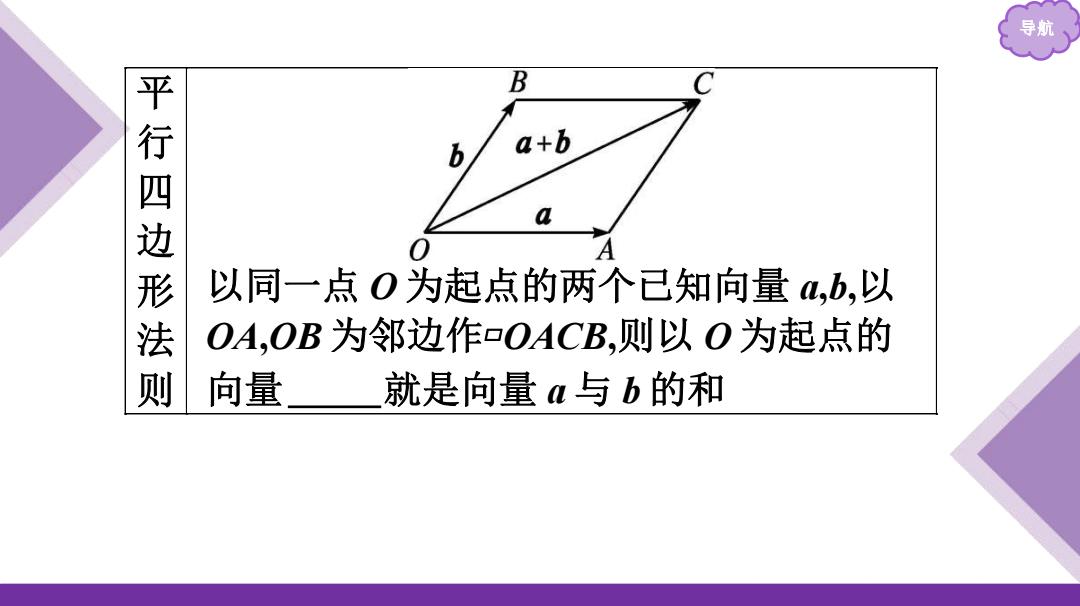
导航 B 平行四边形法 b a+b 0 0 A 以同一点O为起点的两个已知向量,b,以 OA,OB为邻边作口OACB,则以O为起点的 向量 就是向量a与b的和
导航 平 行 四 边 形 法 则 以同一点 O 为起点的两个已知向量 a,b,以 OA,OB 为邻边作▱OACB,则以 O 为起点的 向量 𝑶 𝑪 就是向量 a 与 b 的和
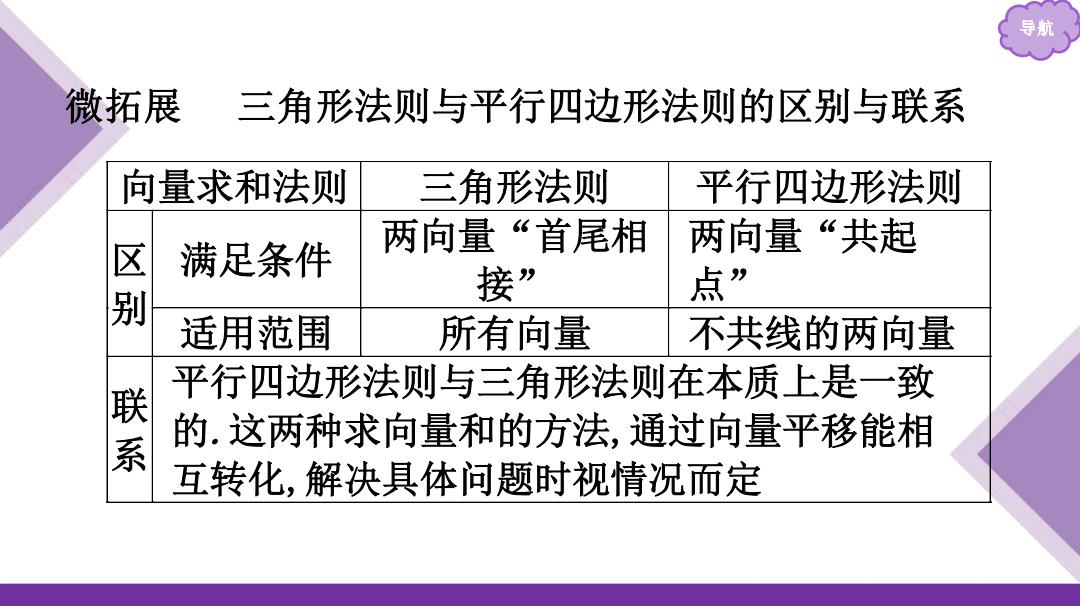
微拓展 三角形法则与平行四边形法则的区别与联系 向量求和法则 三角形法则 平行四边形法则 两向量“首尾相 两向量“共起 区 满足条件 别 接” 点” 适用范围 所有向量 不共线的两向量 联 平行四边形法则与三角形法则在本质上是一致 的.这两种求向量和的方法,通过向量平移能相 互转化,解决具体问题时视情况而定
导航 微拓展 三角形法则与平行四边形法则的区别与联系 向量求和法则 三角形法则 平行四边形法则 区 别 满足条件 两向量“首尾相 接” 两向量“共起 点” 适用范围 所有向量 不共线的两向量 联 系 平行四边形法则与三角形法则在本质上是一致 的.这两种求向量和的方法,通过向量平移能相 互转化,解决具体问题时视情况而定

微思考1两个向量相加就是这两个向量的模相加吗? 提示:不是,向量相加要考虑大小及方向,而模相加只是数量的 加法 3.+b1与d,lb之间的关系 一般地,我们有a+b_d+bl,当且仅当a,b 时等号 成立 4.向量加法的运算律 (1)交换律:a+b= (2)结合律:(+b)+c= 微思考2向量加法的运算律与实数加法的运算律相同吗? 提示:相同
微思考 导航 1 两个向量相加就是这两个向量的模相加吗? 提示:不是,向量相加要考虑大小及方向,而模相加只是数量的 加法. 3.|a+b|与|a|,|b|之间的关系 一般地,我们有|a+b| ≤ |a|+|b|,当且仅当a,b 方向相同 时等号 成立. 4.向量加法的运算律 (1)交换律:a+b= b+a . (2)结合律:(a+b)+c= a+(b+c) . 微思考2 向量加法的运算律与实数加法的运算律相同吗? 提示:相同

导航 课堂·重难突破 向量加法的三角形法则和平行四边形法则 典例剖析 1.(1)如图,在△ABC中,D,E分别是 AB,AC上的点,F为线段DE延长线上的 点,DE∥BC,AB∥CF,连接CD,那么 (在横线上只填一个向量): B ①AB+DF=AD+F元=AD+BC+FC=
导航 课堂·重难突破 一 向量加法的三角形法则和平行四边形法则 典例剖析 1.(1)如图,在△ABC中,D,E分别是 AB,AC上的点,F为线段DE延长线上的 点,DE∥BC,AB∥CF,连接CD,那么 (在横线上只填一个向量): ①𝐴 𝐵 +𝐷 𝐹 = 𝐴 𝐷 +𝐹 𝐶 = 𝐴 𝐷 +𝐵 𝐶 +𝐹 𝐶 =

导航 答案:①AC②AB ③AC 解析:根据题图及己知可得四边形DFCB为平行四边形, 由向量加法的运算法则可知: ①AB+DF=AB+BC=AC ②AD+FC=AD+DB=AB. AD+BC+FC-AD+DE+FC-AC
导航 答案:① AC ② AB ③ AC 解析:根据题图及已知可得四边形 DFCB 为平行四边形, 由向量加法的运算法则可知: ①𝐴 𝐵 +𝐷 𝐹 =𝐴 𝐵 +𝐵 𝐶 =𝐴 𝐶 . ②𝐴 𝐷 +𝐹 𝐶 =𝐴 𝐷 +𝐷 𝐵 =𝐴 𝐵 . ③𝐴 𝐷 +𝐵 𝐶 +𝐹 𝐶 =𝐴 𝐷 +𝐷 𝐹 +𝐹 𝐶 =𝐴 𝐶
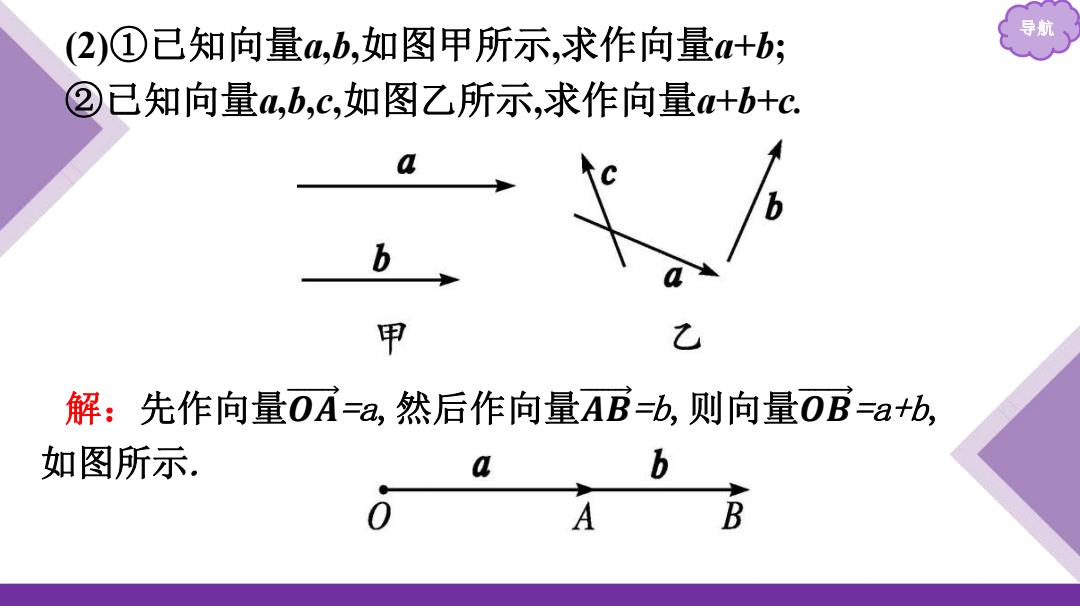
(2)①已知向量a,b,如图甲所示,求作向量a+b; 导航 ②已知向量a,b,c,如图乙所示,求作向量a+b+c. a b 甲 解:先作向量0A=a,然后作向量AB=b,则向量0B=a+b, 如图所示 a b 0 A B
导航 (2)①已知向量a,b,如图甲所示,求作向量a+b; ②已知向量a,b,c,如图乙所示,求作向量a+b+c. 解:先作向量 𝑶 𝑨 =a,然后作向量 𝑨 𝑩 =b,则向量 𝑶 𝑩 =a+b, 如图所示