
全程设计 7.1.2 复数的几何意义
7.1.2 复数的几何意义

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 1.复平面 建立直角坐标系来表示复数的平面叫做复平面,x轴叫做 轴叫做 .实轴上的点都表示实数;除了 外,虚轴上的点都表示纯虚数
导航 课前·基础认知 1.复平面 建立直角坐标系来表示复数的平面叫做复平面,x轴叫做 实轴 ,y轴叫做 虚轴 .实轴上的点都表示实数;除了 原 点 外,虚轴上的点都表示纯虚数
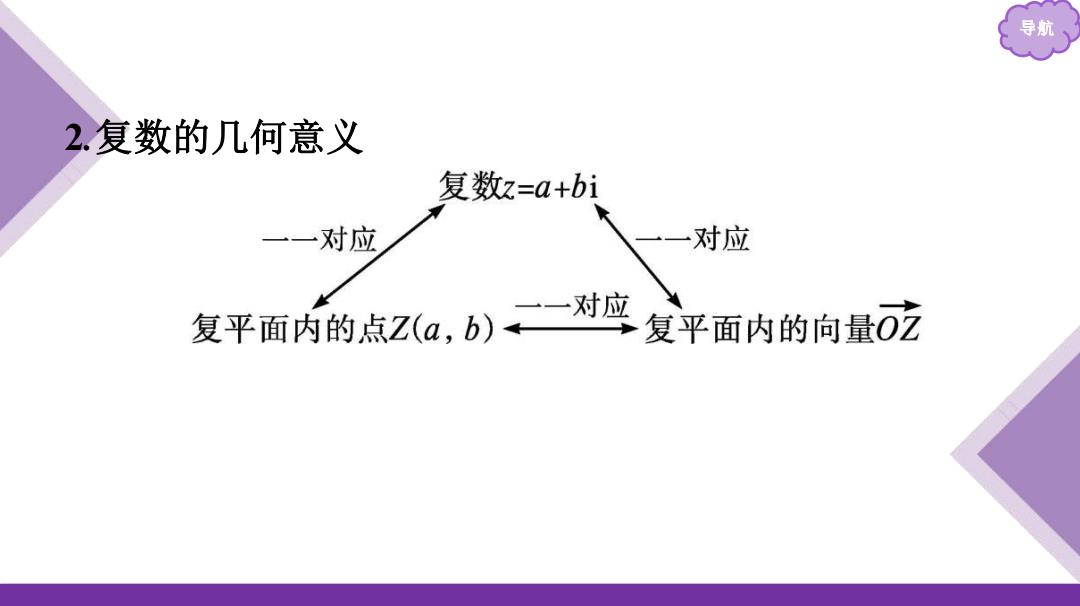
导航 2.复数的几何意义 复数z=a+bi 一一对应 一一对应 复平面内的点Za,b)二对应 复平面内的向量0立
导航 2 .复数的几何意义
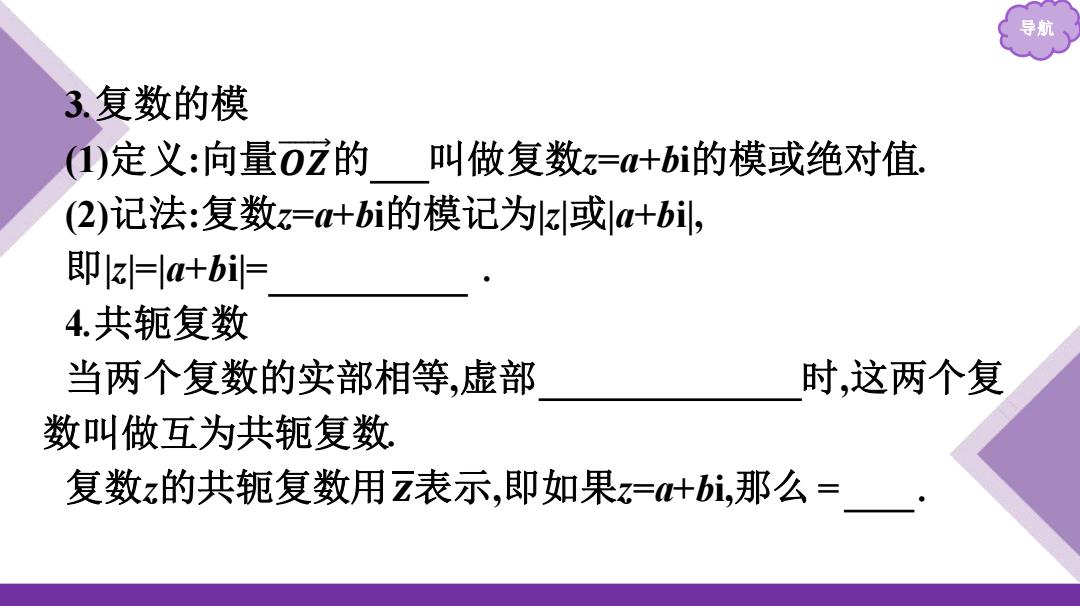
导 3复数的模 )定义:向量0z的 叫做复数z=a+bi的模或绝对值: (2)记法:复数z=叶bi的模记为z或a+bi, 即z=la+bi= 4.共轭复数 当两个复数的实部相等,虚部 时,这两个复 数叫做互为共轭复数 复数z的共轭复数用z表示,即如果z=+bi,那么=
导航 3.复数的模 (1)定义:向量 的 模 叫做复数z=a+bi的模或绝对值. (2)记法:复数z=a+bi的模记为|z|或|a+bi|, 即|z|=|a+bi|= . 4.共轭复数 当两个复数的实部相等,虚部 互为相反数 时,这两个复 数叫做互为共轭复数. 复数z的共轭复数用 表示,即如果z=a+bi,那么 = a-bi . 𝑎 2 + 𝑏 2 𝒛 𝑶 𝒁

导航 微提醒设R>>0,则根据复数模的几何意义可知: (1)z=R表示以原点为圆心,半径为R的圆. (2)<R表示以原点为圆心,半径为R的圆面(不含边界线) 3)<<R表示以原点为圆心,介于半径为r的小圆和半径为 R的大圆之间的圆环(不含边界线)
导航 微提醒 设R>r>0,则根据复数模的几何意义可知: (1)|z|=R表示以原点为圆心,半径为R的圆. (2)|z|<R表示以原点为圆心,半径为R的圆面(不含边界线). (3)r<|z|<R表示以原点为圆心,介于半径为r的小圆和半径为 R的大圆之间的圆环(不含边界线)

导航 课堂·重难突破 复数与复平面内的点的对应关系 典例剖析 a2-a-6 1当实数分别取何值时,复数z=a十3 +(a2-2-15)i(a∈R) 对应的点Z满足下列条件? ()在复平面的第二象限内; (2)在复平面内的x轴上方
导航 课堂·重难突破 一 复数与复平面内的点的对应关系 典例剖析 1.当实数a分别取何值时,复数z= +(a 2 -2a-15)i(a∈R) 对应的点Z满足下列条件? (1)在复平面的第二象限内; (2)在复平面内的x轴上方. 𝒂 𝟐 -𝒂-𝟔 𝒂 + 𝟑

导航 解:(1)若点Z在复平面的第二象限内, (a2-a-6 则} a+3 0, 解得<-3. (2)若点Z在x轴上方, 则g180 解得心5或<-3
导航 解:(1)若点 Z 在复平面的第二象限内, 则 𝒂 𝟐-𝒂-𝟔 𝒂+𝟑 𝟎, 解得 a 𝟎, 𝒂 + 𝟑 ≠ 𝟎, 解得 a>5 或 a<-3

导航 规律总结利用复数与点的对应关系解题的步骤 (1)确定复数的实部与虚部,从而确定复数对应点的横、纵坐 标 (2)根据已知条件,确定实部与虚部满足的关系:
导航 规律总结 利用复数与点的对应关系解题的步骤 (1)确定复数的实部与虚部,从而确定复数对应点的横、纵坐 标. (2)根据已知条件,确定实部与虚部满足的关系

导 二复数与复平面内的向量的对应关系 典例剖析 2.在复平面内,点A,B,C对应的复数分别为1+4i,-3i,2,O为复平 面的坐标原点. (1)求向量OA+OB和AC对应的复数; (2)求平行四边形ABCD的顶点D对应的复数
导航 二 复数与复平面内的向量的对应关系 典例剖析 2.在复平面内,点A,B,C对应的复数分别为1+4i,-3i,2,O为复平 面的坐标原点. (1)求向量 对应的复数; (2)求平行四边形ABCD的顶点D对应的复数. 𝑶 𝑨 + 𝑶 𝑩 和𝑨 𝑪