
全程设计 第2课时 直线与平面垂直的性质定理
第2课时 直线与平面垂直的性质定理

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破
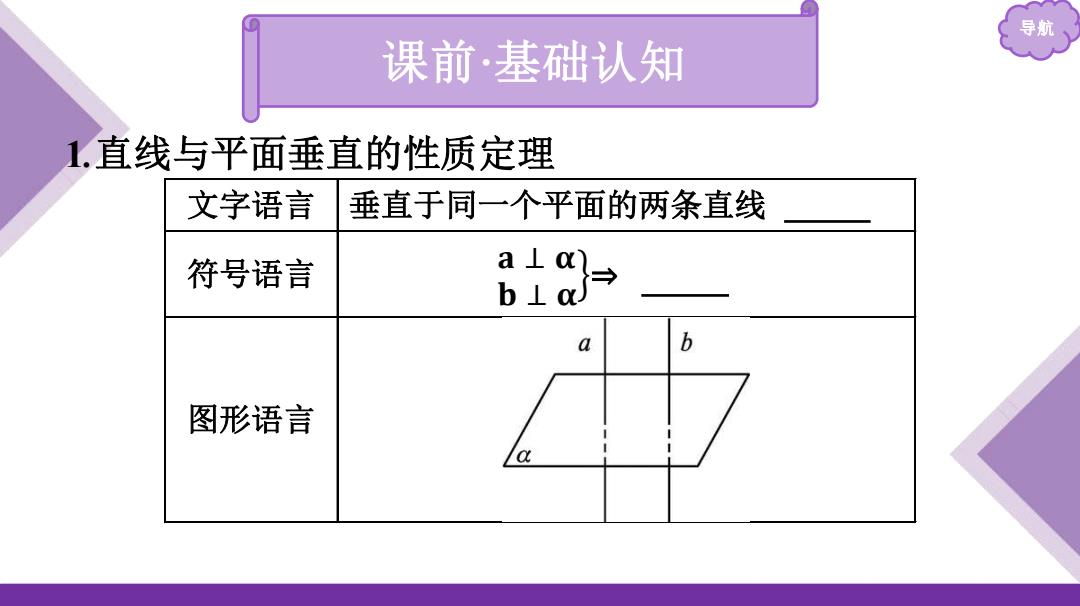
导航 课前·基础认知 1.直线与平面垂直的性质定理 文字语言 垂直于同一个平面的两条直线 符号语言 a⊥o a b 图形语言
导航 课前 ·基础认知 1 .直线与平面垂直的性质定理 文字语言 垂直于同一个平面的两条直线 平行 符号语言 𝐚 ⊥ 𝛂 𝐛 ⊥ 𝛂 ⇒ a ∥ b 图形语言

导航 微思考 如果两个平面都垂直于一条直线,那么这两个平面有 什么关系? 提示:平行 2.直线与平面、平面与平面的距离 (1)直线与平面的距离 一条直线与一个平面平行时,这条直线上 到这个平 面的距离,叫做这条直线到这个平面的距离: (2)平面与平面的距离 如果两个平面平行,那么其中一个平面内的任意一点到另 平面的距离都,我们把它叫做这两个平行平面间的距离
导航 微思考 如果两个平面都垂直于一条直线,那么这两个平面有 什么关系? 提示:平行. 2.直线与平面、平面与平面的距离 (1)直线与平面的距离 一条直线与一个平面平行时,这条直线上 任意一点 到这个平 面的距离,叫做这条直线到这个平面的距离. (2)平面与平面的距离 如果两个平面平行,那么其中一个平面内的任意一点到另一个 平面的距离都 相等 ,我们把它叫做这两个平行平面间的距离
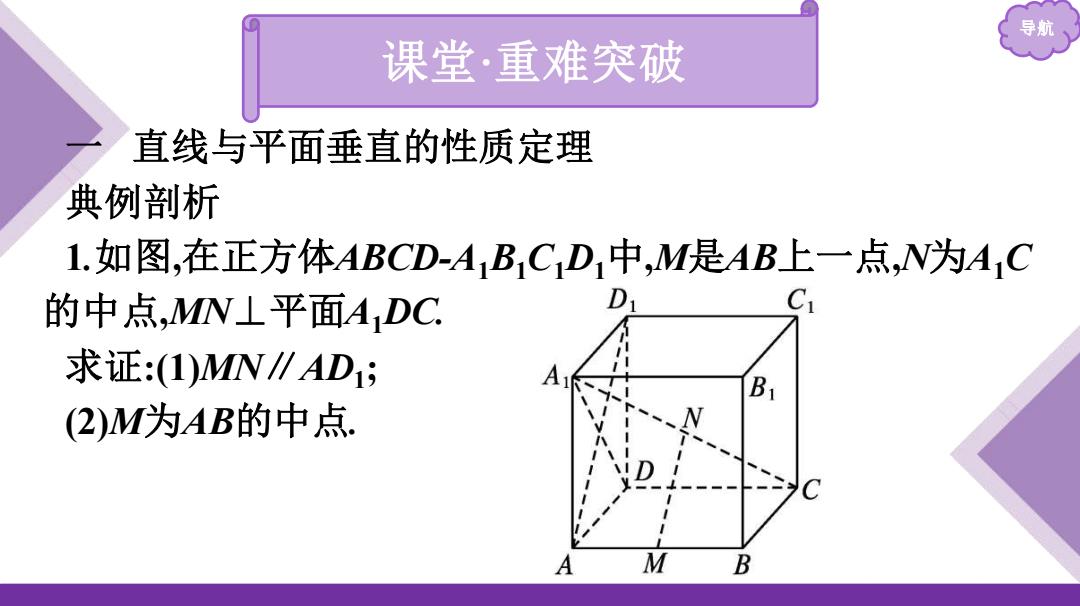
导航 课堂·重难突破 直线与平面垂直的性质定理 典例剖析 1.如图,在正方体ABCD-A1B1C1D1中,M是AB上一点,N为A1C 的中点,MN⊥平面ADC. C 求证:(1)MN∥AD; A (2)M为AB的中点 A M B
导航 课堂·重难突破 一 直线与平面垂直的性质定理 典例剖析 1.如图,在正方体ABCD-A1B1C1D1中,M是AB上一点,N为A1C 的中点,MN⊥平面A1DC. 求证:(1)MN∥AD1 ; (2)M为AB的中点

导航 证明:(1).四边形ADD1A1为正方形,∴.AD1⊥A1D 又CD⊥平面ADDA,∴.CD⊥AD1 又AD∩CD=D,∴.AD1⊥平面ADC 又MN⊥平面ADC,.MN∥AD· (2)设A1D与AD1交于点O,连接ON(图略), 由题意可知,O为AD的中点 :N为AC的中点:ON∥CD/AB,.ON2CD-2AB又 MN∥AD1,'.四边形AMNO为平行四边形, .OW=AM,AM=号AB,即M为AB的中点
导航 证明:(1)∵四边形ADD1A1为正方形,∴AD1⊥A1D. 又CD⊥平面ADD1A1 ,∴CD⊥AD1 . 又A1D∩CD=D,∴AD1⊥平面A1DC. 又MN⊥平面A1DC,∴MN∥AD1 . (2)设A1D与AD1交于点O,连接ON(图略), 由题意可知,O为A1D的中点. ∵N为A1C的中点,∴ON∥CD∥AB,ON= CD= AB.又 MN∥AD1 ,∴四边形AMNO为平行四边形, ∴ON=AM,∴AM= AB,即M为AB的中点. 𝟏 𝟐 𝟏 𝟐 𝟏 𝟐

导航 规律总结证明线线平行的方法: )利用线线平行的定义; (2)利用基本事实4; (3)利用线面平行的性质定理; (4)利用面面平行的性质定理; (⑤)利用线面垂直的性质定理
导航 规律总结 证明线线平行的方法 : (1)利用线线平行的定义 ; (2)利用基本事实 4 ; (3 )利用线面平行的性质定理 ; (4)利用面面平行的性质定理 ; (5)利用线面垂直的性质定理

导航 二空间中的距离问题 典例剖析 2.如图,长方体ABCD-A1B1C1D1的底面ABCD是正方形,点E 在棱AA1上,BE⊥EC,若AE=A1E,AB=3,求四棱锥E-BB1C1C的 体积. D A E D B
导航 二 空间中的距离问题 典例剖析 2.如图,长方体ABCD-A1B1C1D1的底面ABCD是正方形,点E 在棱AA1上,BE⊥EC1 .若AE=A1E,AB=3,求四棱锥E-BB1C1C的 体积

解:在长方体ABCD-A1B1C1D1中,B1C1⊥平面ABB1A1,BEC平航 面ABB1A1,所以B1C1⊥BE. 因为BE⊥EC1,BC∩EC=C1,所以BE⊥平面EB,C,所以 BE⊥EB1,即∠BEB1=90°. 由题意可知Rt△ABE≌Rt△A1B,E, 所以∠AEB=∠A1EB1=45°,所以AE=AB=3,AA1=2AE=6. 因为在长方体ABCD-A1B1C1D1中,AA1∥平面 BB1C1C,E∈AA1,AB⊥平面BB1C1C,AB=3, 所以点E到平面BB1C1C的距离等于点A到平面BB,C1C的距离, 即点E到平面BB1C1C的距离为3, 所以四棱锥E-BB1C1C的体积=3X3X6X3=18
解:在长方体ABCD-A 导航 1B1C1D1中,B1C1⊥平面ABB1A1 ,BE⊂平 面ABB1A1 ,所以B1C1⊥BE. 因为BE⊥EC1 ,B1C1∩EC1=C1 ,所以BE⊥平面EB1C1 ,所以 BE⊥EB1 ,即∠BEB1=90° . 由题意可知Rt△ABE≌Rt△A1B1E, 所以∠AEB=∠A1EB1=45° ,所以AE=AB=3,AA1=2AE=6. 因为在长方体ABCD-A1B1C1D1中,AA1∥平面 BB1C1C,E∈AA1 ,AB⊥平面BB1C1C,AB=3, 所以点E到平面BB1C1C的距离等于点A到平面BB1C1C的距离, 即点E到平面BB1C1C的距离为3, 所以四棱锥E-BB1C1C的体积V= ×3×6×3=18. 𝟏 𝟑

导航 规律总结点到平面的距离可转化为直线到平面的距离,也 可转化为两平行平面间的距离注意点到平面的距离、直线 到平面的距离、两平行平面间的距离互相转化的条件
导航 规律总结 点到平面的距离可转化为直线到平面的距离,也 可转化为两平行平面间的距离.注意点到平面的距离、直线 到平面的距离、两平行平面间的距离互相转化的条件