
全程设计 1.4.1用空间向量研究直线、平面的位置关系 第1课时 用空间向量研究直线、平面的平行关系
1.4.1 用空间向量研究直线、平面的位置关系 第1课时 用空间向量研究直线、平面的平行关系

素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练

导航 素养·目标定位 目标素养 知识概览 1.能用向量语言描述直线和 点的位置向量 平面,理解直线的方向向量 用空间向量 空间直线的向量表示式 与平面的法向量. 研究直线、 平面的平行 空间平面的向量表示式 2.会求平面的法向量 关系 平面的法向量 证明线线平行 3.能用向量方法证明直线、 用向量方法证 明直线、平面 证明线面平行 平面的平行关系 的平行关系 证明面面平行
导航 素养·目标定位 目 标 素 养 知 识 概 览 1.能用向量语言描述直线和 平面,理解直线的方向向量 与平面的法向量. 2.会求平面的法向量. 3.能用向量方法证明直线、 平面的平行关系

导航 课前·基础认知 1点的位置向量 在空间中,取一定点O作为基点,那么空间中任意一点P就可以 用向量0P来表示我们把向量0P称为点P的位置向 量
导航 课前·基础认知 1.点的位置向量 在空间中,取一定点O作为基点,那么空间中任意一点P就可以 用向量 来表示.我们把向量 称为点P的位置向 量. 𝑶 𝑷 𝑶 𝑷
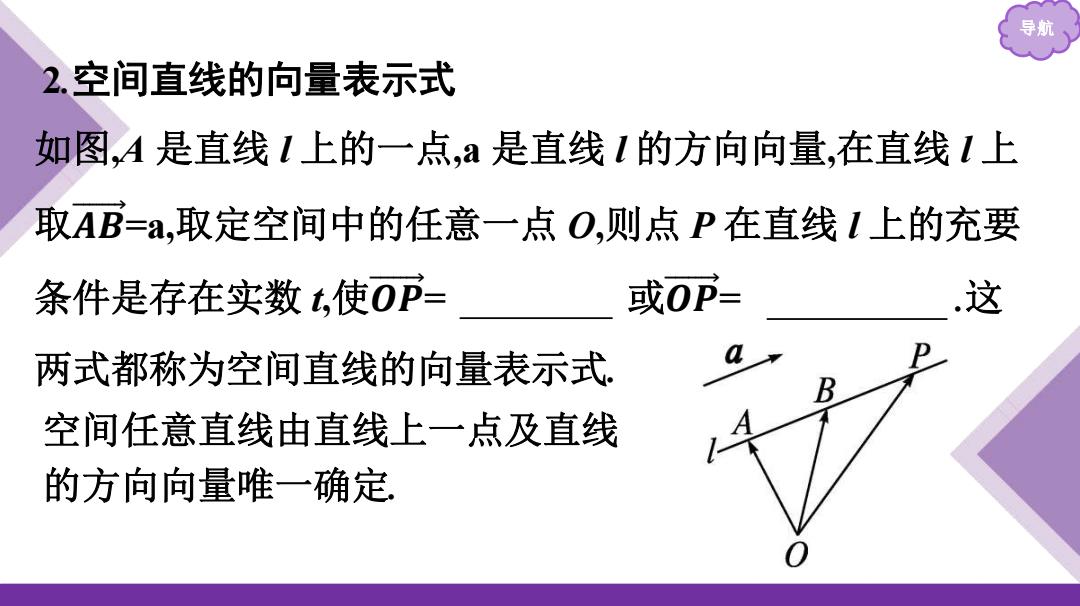
导月 2.空间直线的向量表示式 如图,A是直线1上的一点,a是直线1的方向向量,在直线1上 取AB=a,取定空间中的任意一点O,则点P在直线l上的充要 条件是存在实数t,使OP= 或OP= 这 两式都称为空间直线的向量表示式。 空间任意直线由直线上一点及直线 的方向向量唯一确定
导航 2.空间直线的向量表示式 如图,A 是直线 l 上的一点,a 是直线 l 的方向向量,在直线 l 上 取𝑨 𝑩 =a,取定空间中的任意一点 O,则点 P 在直线 l 上的充要 条件是存在实数 t,使𝑶 𝑷 = 𝑶 𝑨 +ta 或𝑶 𝑷 = 𝑶 𝑨 +t𝑨 𝑩 .这 两式都称为空间直线的向量表示式. 空间任意直线由直线上一点及直线 的方向向量唯一确定
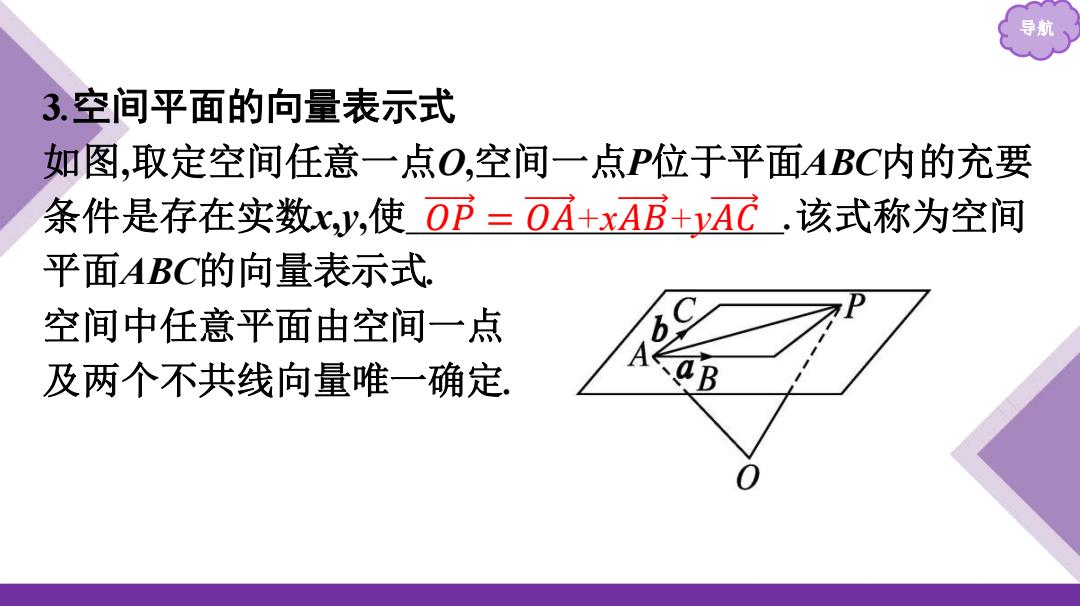
导航 3.空间平面的向量表示式 如图,取定空间任意一点O,空间一点P位于平面ABC内的充要 条件是存在实数x,y,使OP=OA+xAB+AC.该式称为空间 平面ABC的向量表示式 空间中任意平面由空间一点 及两个不共线向量唯一确定
导航 3.空间平面的向量表示式 如图,取定空间任意一点O,空间一点P位于平面ABC内的充要 条件是存在实数x,y,使 .该式称为空间 平面ABC的向量表示式. 空间中任意平面由空间一点 及两个不共线向量唯一确定. 𝑂 𝑃 = 𝑂 𝐴 +x𝐴 𝐵 +y𝐴 𝐶

导航 4.平面的法向量 如图,直线l⊥,取直线的方向向量a,我们称向量a为平面a的 法向量.给定一个点A和一个向量a,那么过点A,且以向量a为法 向量的平面完全确定,可以表示为集合PaA卫0!, a
导航 4.平面的法向量 如图,直线l⊥α,取直线l的方向向量a,我们称向量a为平面α的 法向量.给定一个点A和一个向量a,那么过点A,且以向量a为法 向量的平面完全确定,可以表示为集合 {P|a·𝐴 𝑃 =0}

导航 微思考一个平面的法向量是唯一确定的吗? 提示:不是
导航 微思考一个平面的法向量是唯一确定的吗? 提示:不是
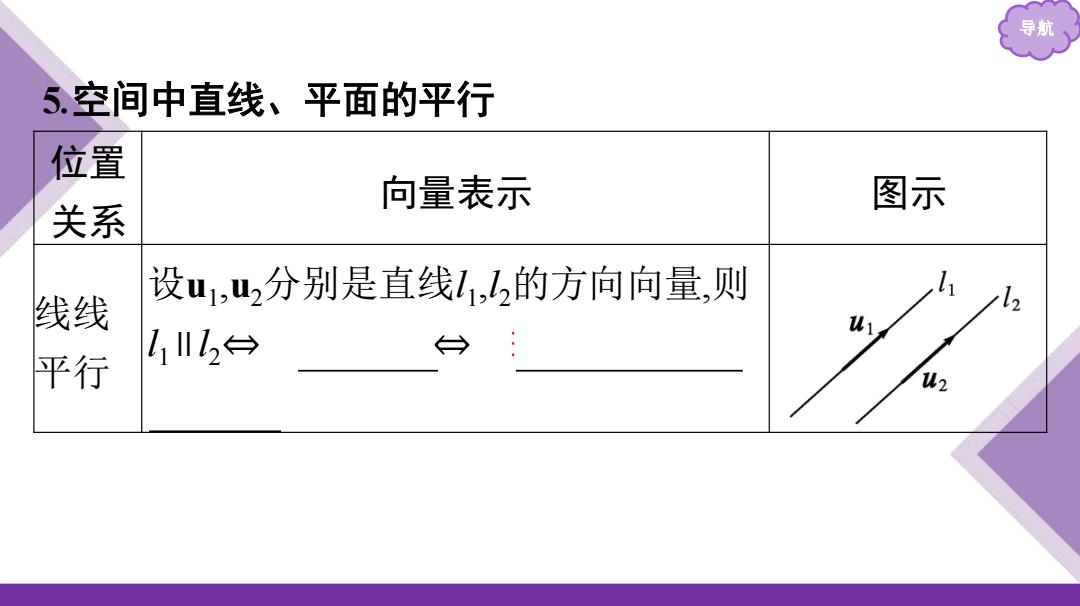
导航 5空间中直线、平面的平行 位置 向量表示 图示 关系 设u1,2分别是直线1,2的方向向量,则 h 线线 M 平行 11川12台 u2
导航 5.空间中直线、平面的平行 位置 关系 向量表示 图示 线线 平行 设u1 ,u2分别是直线l1 ,l2的方向向量,则 l1∥l2⇔ u1∥u2 ⇔ ∃λ∈R,使得 u1 =λu2
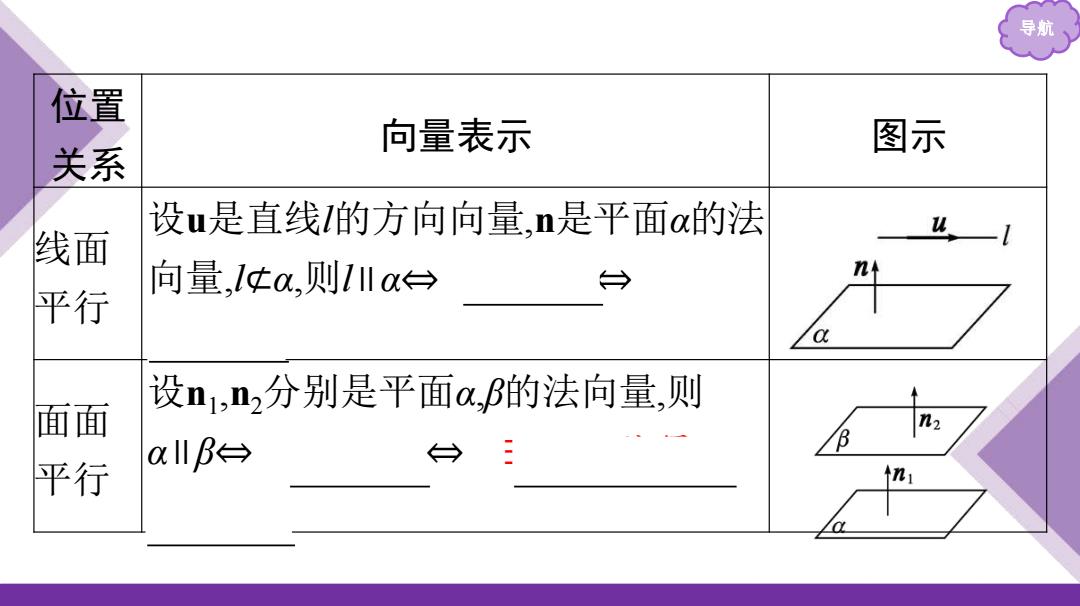
导航 位置 向量表示 图示 关系 设u是直线的方向向量,n是平面a的法 线面 向量,1¢a,则1I川o台 → 平行 设n1,n2分别是平面a,的法向量,则 面面 n2 allB台 ←→ 平行 in
导航 位置 关系 向量表示 图示 线面 平行 设 u是直线 l的方向向量 , n是平面 α的法 向量 , l ⊄ α , 则 l ∥ α ⇔ u ⊥ n ⇔ u · n = 0 面面 平行 设 n 1 , n 2分别是平面 α ,β的法向量 , 则 α ∥ β ⇔ n 1 ∥ n 2 ⇔ ∃ λ ∈R,使得 n 1 = λ n 2