
全程设计 2.1直线的倾斜角与斜率 2.1.1 倾斜确与斜率
2.1 直线的倾斜角与斜率 2.1.1 倾斜角与斜率
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练

导 素养·目标定位 目标素养 1.在平面直角坐标系中,结合具体图形,探索确定直线位置的 几何要素 2.理解直线的倾斜角和斜率的概念. 3.经历用代数法刻画直线斜率的过程,掌握过两点的直线斜 率的计算公式。 4.掌握倾斜角与斜率的对应关系
导航 素养·目标定位 目 标 素 养 1.在平面直角坐标系中,结合具体图形,探索确定直线位置的 几何要素. 2.理解直线的倾斜角和斜率的概念. 3.经历用代数法刻画直线斜率的过程,掌握过两点的直线斜 率的计算公式. 4.掌握倾斜角与斜率的对应关系
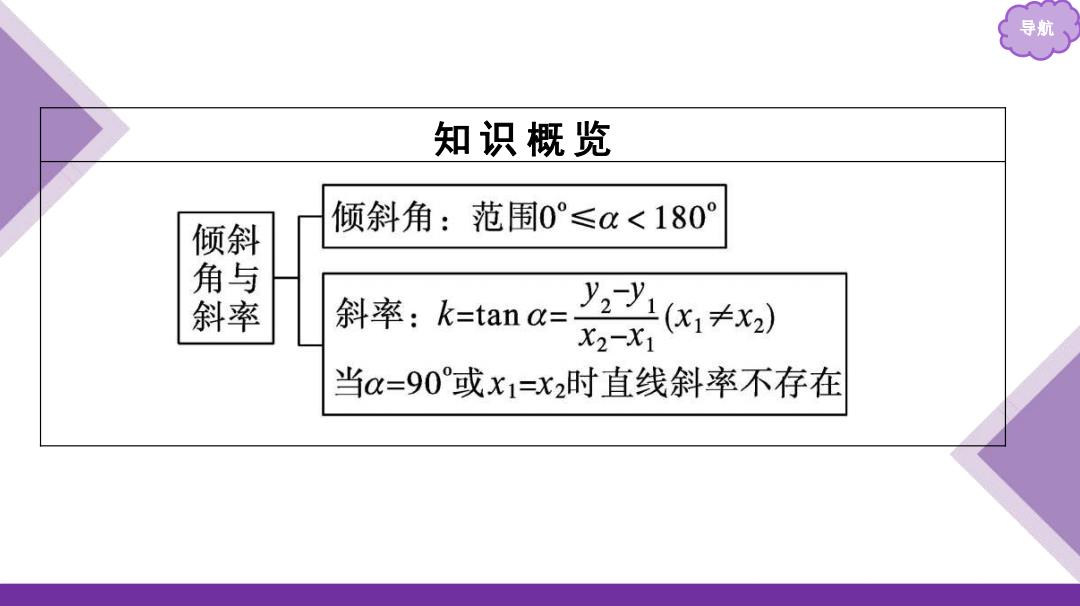
导航 知识概览 倾斜角:范围0°≤a<180 倾斜 角与 斜率 斜率:k=tana=y, (1≠x2) X2-X1 当au=90°或x1=x2时直线斜率不存在
导航 知 识 概 览

导 课前·基础认知 1.直线的倾斜角 (1)倾斜角的定义:当直线l与x轴相交时,我们以x轴为基准,x轴 与直线l 的方向之间所成的角α叫做直线的 倾斜角. (2)倾斜角的范围:当直线与x轴平行或重合时,我们规定它的 倾斜角为 直线的倾斜角α的取值范围为
导航 课前·基础认知 1.直线的倾斜角 (1)倾斜角的定义:当直线l与x轴相交时,我们以x轴为基准,x轴 正向 与直线l 向上 的方向之间所成的角α叫做直线l的 倾斜角. (2)倾斜角的范围:当直线l与x轴平行或重合时,我们规定它的 倾斜角为 0° ,直线的倾斜角α的取值范围为 0°≤α<180°

2.直线的斜率 (1)斜率的定义:一条直线的倾斜角a的 值叫做这条 直线的斜率斜率常用小写字母k表示,即= 倾斜角是 的直线没有斜率,倾斜角不是90°的直线都 有斜率 (2)斜率公式:如果直线经过两点P1(c1y1),P2(K2y2)K1x2),那么 y2-y1 可得斜率公式为= X2-X1 3)倾斜角与斜率的作用:在平面直角坐标系中,倾斜角与斜率 分别从形和数两个角度刻画了直线相对于x轴的倾斜程度
导航 2.直线的斜率 (1)斜率的定义:一条直线的倾斜角α的 正切 值叫做这条 直线的斜率.斜率常用小写字母k表示,即k= tan α . 倾斜角是 90° 的直线没有斜率,倾斜角不是90°的直线都 有斜率. (2)斜率公式:如果直线经过两点P1 (x1 ,y1 ),P2 (x2 ,y2 )(x1≠x2 ),那么 可得斜率公式为k= . (3)倾斜角与斜率的作用:在平面直角坐标系中,倾斜角与斜率 分别从形和数两个角度刻画了直线相对于x轴的倾斜程度. 𝑦2 -𝑦1 𝑥2-𝑥1

导航 微思考(1)只给出倾斜角能确定一条直线吗? (2)当一条直线的倾斜角为0°时,这条直线一定与x轴平行吗? 提示:)不能倾斜角只能确定直线的方向,要确定直线还需知 道直线上的一个点 (2)不一定,也可能与x轴重合
导航 微思考 (1)只给出倾斜角能确定一条直线吗? (2)当一条直线的倾斜角为0°时,这条直线一定与x轴平行吗? 提示:(1)不能.倾斜角只能确定直线的方向,要确定直线还需知 道直线上的一个点. (2)不一定,也可能与x轴重合

导期 课堂·重难突破 求直线的倾斜角 典例剖析 1.设直线过原点,其倾斜角为α,将直线绕坐标原点沿逆时针 方向旋转45°得到直线L,则直线l的倾斜角为(D) A.a+45° B.a-135° C.135°-a D.当0°≤a<135时,倾斜角为a+45°,当135°≤a<180°时,倾斜 角为a-135°
导航 课堂·重难突破 一 求直线的倾斜角 典例剖析 1.设直线l过原点,其倾斜角为α,将直线l绕坐标原点沿逆时针 方向旋转45°得到直线l1 ,则直线l1的倾斜角为( ) A.α+45° B.α-135° C.135°-α D.当0°≤α<135°时,倾斜角为α+45° ,当135°≤α<180°时,倾斜 角为α-135° D
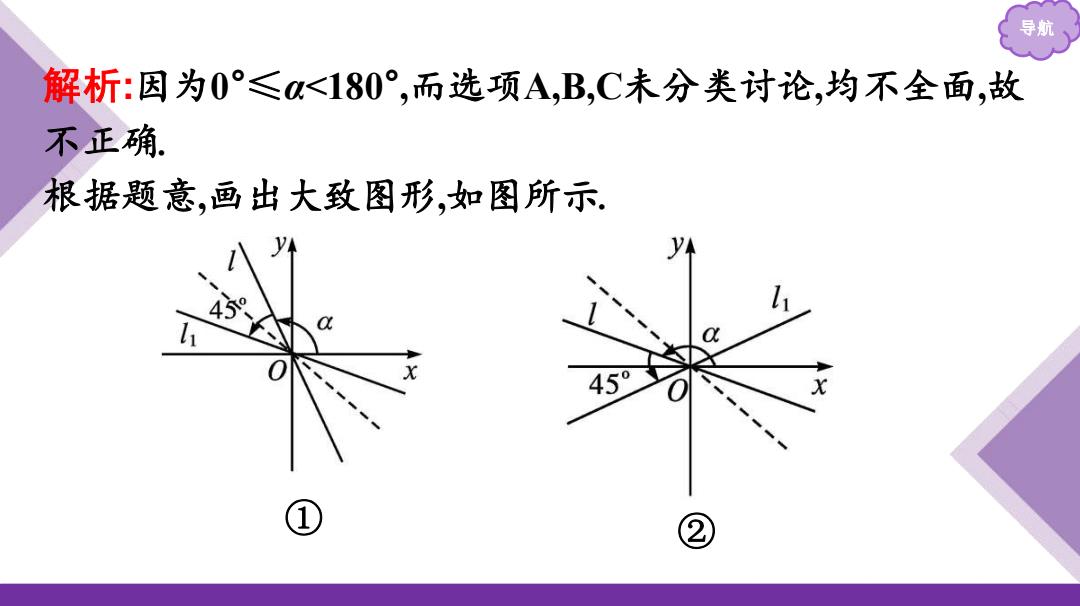
导航 解析:因为0°≤a<180°,而选项A,B,C未分类讨论,均不全面,故 不正确 根据题意,画出大致图形,如图所示 1】 45 459 ① ②
导航 解析:因为0°≤α<180° ,而选项A,B,C未分类讨论,均不全面,故 不正确. 根据题意,画出大致图形,如图所示. ① ②

导航 当0°≤a<135°时,直线l1的倾斜角为a+45°,如图①所示; 当135°≤a<180°时,直线1,的倾斜角为45°+a-180° =0-135°,如图②所示. 故选D
导航 当0°≤α<135°时,直线l1的倾斜角为α+45° ,如图①所示; 当135°≤α<180°时,直线l1的倾斜角为45°+α-180° =α-135° ,如图②所示. 故选D