
全程设计 6.2 排列与组合 第1课时 排列与排列数
6.2 排列与组合 第1课时 排列与排列数
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随 堂 训 练

导航 素养·目标定位 目标素养 1理解排列、排列数的定义,掌握排列数公式及推导方法 2.能用列举法、树形图法表示出一个排列问题的所有的排列. 3.能用排列数公式解决无限制条件的排列问题
导航 目 标 素 养 1.理解排列、排列数的定义,掌握排列数公式及推导方法. 2.能用列举法、树形图法表示出一个排列问题的所有的排列. 3.能用排列数公式解决无限制条件的排列问题. 素养·目标定位
知识概览 导航 排列 排列数 概念 全排列 排列与 排列数 阶乘 公式 排列数公式
知 识 概 览 导航

导 课前·基础认知 1排列 (1)一般地,从n个不同元素中取出m(m≤n)个元素,并按照 排成一列,叫做从n个不同元素中取出个元素 的一个排列 (2)根据排列的定义,两个排列相同的充要条件是:两个排列 的元素完全 ,且元素的排列顺序也
导航 1.排列 (1)一般地,从n个不同元素中取出m(m≤n)个元素,并按照 一定的顺序 排成一列,叫做从n个不同元素中取出m个元素 的一个排列. (2)根据排列的定义,两个排列相同的充要条件是:两个排列 的元素完全 相同 ,且元素的排列顺序也 相同 . 课前·基础认知

导 微判断(1)若两个排列的元素相同,则这两个排列是相同的 排列.(×) (2)从6名学生中选3名学生参加数学、物理、化学竞赛,共 有多少种选法属于排列问题(√) (3)有12名学生参加植树活动,要求三人一组,共有多少种分 组方案属于排列问题(×)
导航 微判断(1)若两个排列的元素相同,则这两个排列是相同的 排列.( ) (2)从6名学生中选3名学生参加数学、物理、化学竞赛,共 有多少种选法属于排列问题.( ) (3)有12名学生参加植树活动,要求三人一组,共有多少种分 组方案属于排列问题.( ) × √ ×

导航 (4)从3,5,7,9中任取两个数进行指数运算,可以得到多少个幂 属于排列问题(√) (⑤)从1,2,3,4中任取两个数作为点的坐标,可以得到多少个点 属于排列问题(√)
导航 (4)从3,5,7,9中任取两个数进行指数运算,可以得到多少个幂 属于排列问题.( ) (5)从1,2,3,4中任取两个数作为点的坐标,可以得到多少个点 属于排列问题.( ) √ √

导航 2.排列数与排列数公式 从n个不同元素中取出mm≤n)个元素的所有 排列数 叫做从n个不同元素中取出m个元素 的定义 的排列数,用符号 表示 特别地,把n个不同的元素 的一个排列, 全排列 叫做n个元素的一个全排列,用符号 表示 正整数1到n的连乘积,叫做n的 ,用符号 阶乘 表示
导航 2 .排列数与排列数公式 排列数 的定义 从 n 个不同元素中取出 m(m ≤ n)个元素的所有 不同 排列的个数 ,叫做从 n 个不同元素中取出 m 个元素 的排列数,用符号 𝑨 𝐧𝐦 表示 全排列 特别地,把 n 个不同的元素 全部取出 的一个排列, 叫做 n 个元素的一个全排列,用符号 𝑨 𝐧𝐧 表示 阶乘 正整数 1 到 n 的连乘积,叫做 n 的 阶乘 ,用符号 n! 表示
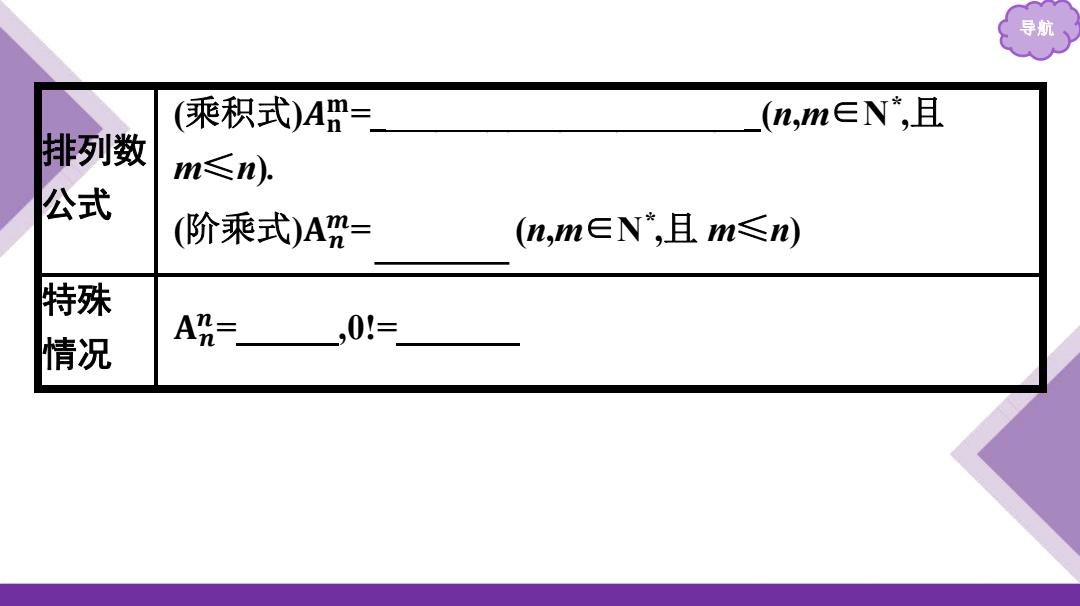
导航 (乘积式)Am= (n,m∈N,且 排列数 m≤n. 公式 (阶乘式)A= (n,m∈N*,且m≤m) 特殊 情况 A7=,01=
导航 排列数 公式 (乘积式)𝑨𝐧 𝐦= n(n-1)(n-2)…(n-m+1) (n,m∈N * ,且 m≤n). (阶乘式)𝐀𝒏 𝒎= 𝒏! (𝒏-𝒎)! (n,m∈N * ,且 m≤n) 特殊 情况 𝐀𝒏 𝒏 = n! ,0!= 1

导航 微思考排列与排列数有何区别? 提示:“排列”是指从n个不同的元素中任取m(m≤n)个元素, 按照一定的顺序排成一列,不是数;“排列数”是指从个不同 元素中取出m(m≤n)个元素的所有排列的个数,是一个数.因 此符号An只表示排列数,而不表示具体的排列
导航 微思考排列与排列数有何区别? 提示:“排列”是指从n个不同的元素中任取m(m≤n)个元素, 按照一定的顺序排成一列,不是数;“排列数”是指从n个不同 元素中取出m(m≤n)个元素的所有排列的个数,是一个数.因 此符号 𝐀𝒏 只表示排列数,而不表示具体的排列. 𝒎