
全程设计 6.2 排列与组合 第3课时 组合与组合数
6.2 排列与组合 第3课时 组合与组合数
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随 堂 训 练

导航 素养·目标定位 目标素养 1.理解组合与组合数的概念 2.会推导组合数公式,并会应用公式求值 3.理解组合数的两个性质,并会化简、求值和证明
导航 目 标 素 养 1.理解组合与组合数的概念. 2.会推导组合数公式,并会应用公式求值. 3.理解组合数的两个性质,并会化简、求值和证明. 素养·目标定位
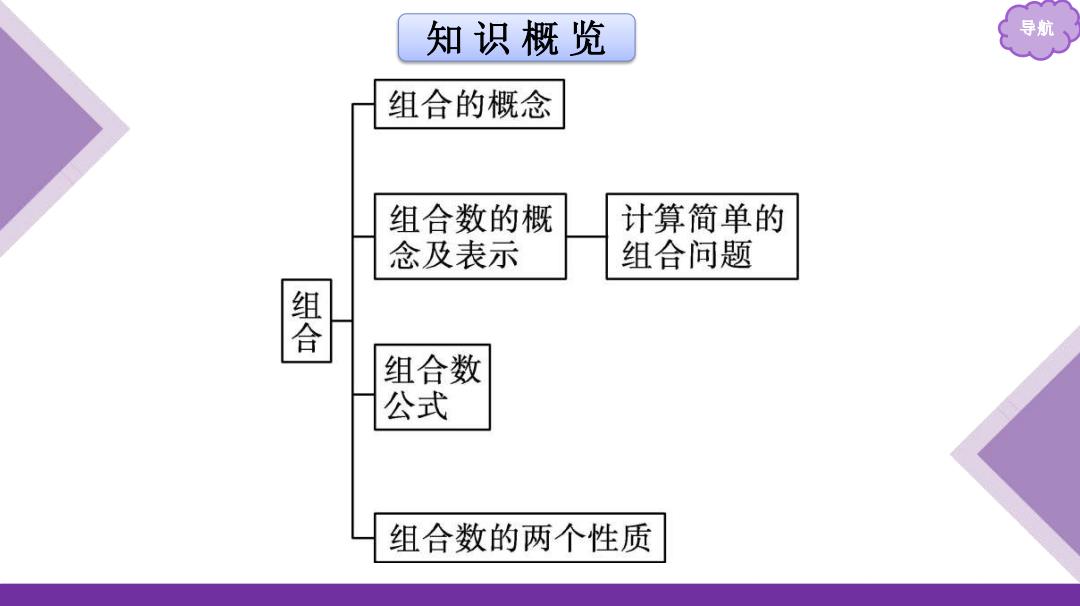
知识概览 导航 组合的概念 组合数的概 计算简单的 念及表示 组合问题 礐 组合数 公式 组合数的两个性质
知 识 概 览 导航

导航 课前·基础认知 1.组合 一般地,从n个不同元素中取出m(m≤m)个元素作为 叫做从n个不同元素中取出m个元素的一个组合
导航 1.组合 一般地,从n个不同元素中取出m(m≤n)个元素作为 一组 , 叫做从n个不同元素中取出m个元素的一个组合. 课前·基础认知

微思考1如何理解组合,它与排列有何区别? 提示:1)组合要求n个元素是不同的,被取出的m个元素也是 不同的,即从n个不同的元素中进行m次不放回地取出, (2)取出的个元素不讲究顺序,也就是说元素没有位置的要 求,无序性是组合的特点 (3)辨别一个问题是排列问题还是组合问题,关键看选出的 元素与顺序是否有关.若交换某一问题中某两个元素的位置 对结果产生影响,则是排列问题,否则就是组合问题
导航 微思考1如何理解组合,它与排列有何区别? 提示:(1)组合要求n个元素是不同的,被取出的m个元素也是 不同的,即从n个不同的元素中进行m次不放回地取出. (2)取出的m个元素不讲究顺序,也就是说元素没有位置的要 求,无序性是组合的特点. (3)辨别一个问题是排列问题还是组合问题,关键看选出的 元素与顺序是否有关.若交换某一问题中某两个元素的位置 对结果产生影响,则是排列问题,否则就是组合问题

2.组合数的概念、公式、性质 导航 从n个不同元素中取出m(m≤m)个元素的 组合数 的个数,叫做从n个不同元素中取出m个元素 定义 的组合数 表示法 CH 组合数 乘积式 Cm= 公式 阶乘式 Cm= 备注 ①n,m∈N,且m≤n;②规定:C=1
导航 2 .组合数的概念、公式、性质 组合数 定义 从 n 个不同元素中取出 m(m ≤ n)个元素的 所有不同 组合 的个数,叫做从 n 个不同元素中取出 m 个元素 的组合数 表示法 𝑪 𝐧𝐦 组合数 公式 乘积式 𝑪 𝐧𝐦 = 𝑨 𝐧𝐦 𝑨 𝐦𝐦 = 𝐧(𝐧-𝟏)( 𝐧-𝟐)…(𝐧-𝐦 + 𝟏) 𝐦! 阶乘式 𝑪 𝐧𝐦 = 𝐧! 𝐦!(𝐧-𝐦)! 备注 ①n,m ∈ N*,且 m ≤ n;②规定:𝐂 𝒏𝟎 =1

微思考2如何理解“组合”与“组合数”这两个概念? 提示:类比“排列”与“排列数”,“组合”与“组合数”也是两个 不同的概念,“组合”是指“从n个不同元素中取m(m≤m个元 素作为一组”,它不是一个数,而是具体的一件事;“组合数”是 指“从n个不同元素中取出m(m≤m)个元素的所有不同组合的 个数”,它是一个数.例如,从3个不同元素,b,c中每次取出两个 元素的组合为b,C,bc,其中每一种都叫一个组合,这些组合共 有3个,则组合数为3
导航 微思考2如何理解“组合”与“组合数”这两个概念? 提示:类比“排列”与“排列数”,“组合”与“组合数”也是两个 不同的概念,“组合”是指“从n个不同元素中取m(m≤n)个元 素作为一组”,它不是一个数,而是具体的一件事;“组合数”是 指“从n个不同元素中取出m(m≤n)个元素的所有不同组合的 个数”,它是一个数.例如,从3个不同元素a,b,c中每次取出两个 元素的组合为ab,ac,bc,其中每一种都叫一个组合,这些组合共 有3个,则组合数为3

,C18= 导航 微训练(1)C名= 答案:1518 解析:c3=袋15c出=c=18 2)方程C4=C4的解为 答案:4或6 X=2x-4, X+2X-4=14, 解析:由题意知2x-4≤14,或2x-4≤14, 解得x=4或6. X≤14 x≤14
导航 答案 :15 18 微训练(1) 𝐂 𝟔𝟐 = ,𝐂 𝟏 𝟖 𝟏 𝟕 = . 解析:𝐂 𝟔𝟐 = 𝟔 × 𝟓 𝟐 × 𝟏 =15, 𝐂 𝟏 𝟖 𝟏 𝟕 = 𝐂 𝟏 𝟖 𝟏 =18. (2)方程 𝐂 𝟏 𝟒 𝒙 = 𝐂 𝟏 𝟒 𝟐 𝒙-𝟒 的解为 . 答案 : 4 或6 解析:由题意知 𝒙 = 𝟐 𝒙-𝟒, 𝟐𝒙-𝟒 ≤ 𝟏𝟒, 𝒙 ≤ 𝟏𝟒 或 𝒙 + 𝟐 𝒙-𝟒 = 𝟏 𝟒, 𝟐𝒙-𝟒 ≤ 𝟏𝟒, 𝒙 ≤ 𝟏𝟒, 解得 x= 4 或 6

导航 课堂·重难突破 组合的概念 典例剖析 1.(1)判断下列问题是组合问题还是排列问题: ①设集合A={a,b,c,山,,则集合A的子集中含有3个元素的有多少个? ②某铁路线上有5个车站,则这条线上共需准备多少种车票?多少 种票价(假设来回的票价相同)? ③2022年元旦期间,某班10名同学互送贺年卡,表示新年的祝福,贺 年卡共有多少张? (2)已知a,b,c,d,五个元素,写出每次取出3个元素的所有组合
导航 一 组合的概念 典例剖析 1.(1)判断下列问题是组合问题还是排列问题: ①设集合A={a,b,c,d,e},则集合A的子集中含有3个元素的有多少个? ②某铁路线上有5个车站,则这条线上共需准备多少种车票?多少 种票价(假设来回的票价相同)? ③2022年元旦期间,某班10名同学互送贺年卡,表示新年的祝福,贺 年卡共有多少张? (2)已知a,b,c,d,e五个元素,写出每次取出3个元素的所有组合. 课堂·重难突破