
全程设计 6.3.2 二项式系数的性质
6.3.2 二项式系数的性质
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随 堂 训 练

导航 素养·目标定位 目标素养 1.学会运用函数观点分析处理二项式系数的性质. 2理解和掌握二项式系数的性质,并能够求解与二项式系数有 关的问题
导航 目 标 素 养 1.学会运用函数观点分析处理二项式系数的性质. 2.理解和掌握二项式系数的性质,并能够求解与二项式系数有 关的问题. 素养·目标定位
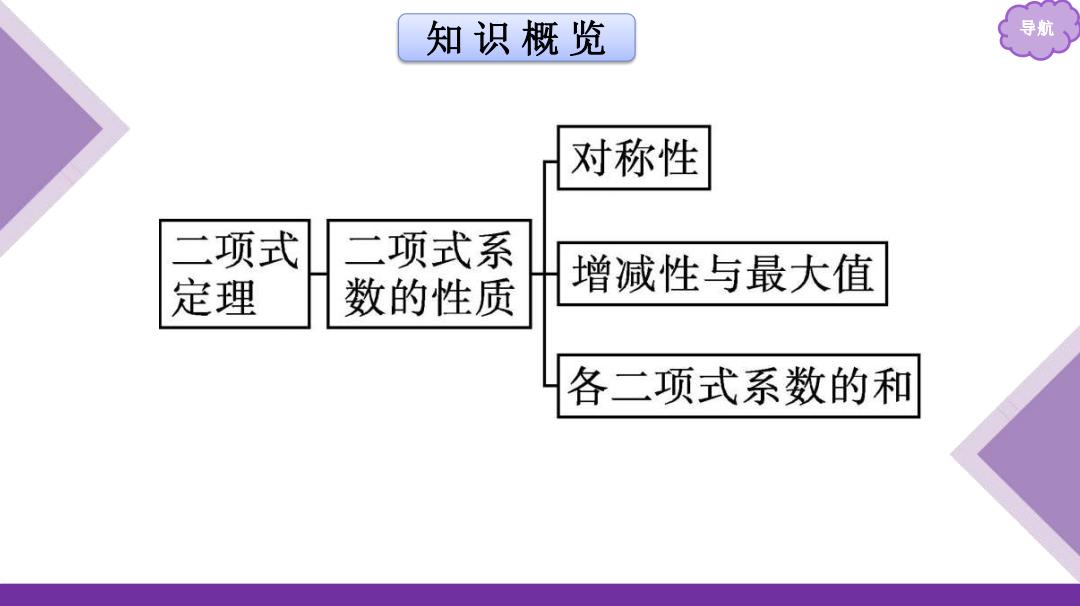
知识概览 导航 对称性 二项式 二项式系 定理 数的性质 增减性与最大值 各二项式系数的和
知 识 概 览 导航

导期 课前·基础认知 1从函数的观点分析二项式系数 对于(+b)”的展开式的二项式系数C%,CC品,…,Ch,可以从函 数的角度分析它们,C可看成以r为自变量的函数r),其定义域 是 2.二项式系数的性质 (1)对称性 与首末两端“等距离”的两个二项式系数 .事实上,这一性 质可直接由 得到
导航 1.从函数的观点分析二项式系数 对于(a+b) n 的展开式的二项式系数𝐂𝒏 𝟎 , 𝐂𝒏 𝟏 , 𝐂𝒏 𝟐 ,…,𝐂𝒏 𝒏 ,可以从函 数的角度分析它们,𝐂𝒏 𝒓 可看成以 r 为自变量的函数 f(r),其定义域 是 {0,1,2,…,n} . 2.二项式系数的性质 (1)对称性 与首末两端“等距离”的两个二项式系数 相等 .事实上,这一性 质可直接由 𝐂𝒏 𝒎 = 𝐂𝒏 𝒏-𝒎 得到. 课前·基础认知

(2)增减性与最大值 当k<时,C随k的增加而增大;由对称性知,当心n时,C随k 2 的增加而减小 当n是偶数时,中间的一项 取得最大值; 当n是奇数时,中间的两项 与 相等,且同时取得 最大值. (3)各二项式系数的和C+C品+C2++C一;C%+C?+ C4+…=C7+C%+C克+…=2m-1
导航 (2)增减性与最大值 当 k𝒏 + 𝟏 𝟐 时,𝐂 𝒏𝒌 随 k 的增加而减小. 当 n 是偶数时,中间的一项 𝐂 𝒏𝒏𝟐 取得最大值; 当 n 是奇数时,中间的两项 𝐂𝒏𝒏-𝟏𝟐 与 𝐂𝒏𝒏+𝟏𝟐 相等,且同时取得 最大值. (3)各二项式系数的和 𝐂 𝒏𝟎 + 𝐂 𝒏𝟏 + 𝐂 𝒏𝟐 + … + 𝐂 𝒏𝒏 = 2 n ;𝐂 𝒏𝟎 + 𝐂 𝒏𝟐 + 𝐂 𝒏𝟒 + … = 𝐂 𝒏𝟏 + 𝐂 𝒏𝟑 + 𝐂 𝒏𝟓 + … = 2 n-1

导 微判断()二项展开式的二项式系数和为Ch+C?+…+C(×) (2)二项展开式中系数最大项与二项式系数最大项相同: (X) (3)(a+b)的展开式中某项的二项式系数是该项中非字母因 数部分,包括符号等(×)
导航 微判断(1)二项展开式的二项式系数和为𝐂𝒏 𝟏 + 𝐂𝒏 𝟐 +…+𝐂𝒏 𝒏 .( ) (2)二项展开式中系数最大项与二项式系数最大项相同. ( ) (3)(a+b) n的展开式中某项的二项式系数是该项中非字母因 数部分,包括符号等.( ) × × ×

导航 课堂·重难突破 求展开式的系数和 典例剖析 1.己知(2x-1)5=r5+ax4+a23+a3x2+a4x+as求: (1)ao+u1+2+…+as; (2)laol+la+lal++asl; (③)a1+u3+us (4)a+2+4; (5)a1+a2+a3t4+as; (6)5a0+4a1+32+2a3+u4
导航 一 求展开式的系数和 典例剖析 1.已知(2x-1)5=a0x 5+a1x 4+a2x 3+a3x 2+a4x+a5 .求: (1)a0+a1+a2+…+a5 ; (2)|a0 |+|a1 |+|a2 |+…+|a5 |; (3)a1+a3+a5 ; (4)a0+a2+a4 ; (5)a1+a2+a3+a4+a5 ; (6)5a0+4a1+3a2+2a3+a4 . 课堂·重难突破

解:(1)令x=1,得ao+a1+2+…+5=1. 导期 (2)令x=-1,得-35=-l0+41-2+3-4+s 由(2x-1)5的通项Tk+1=C5(-1).25-kx5-k知1,3,s为负值, 因此ao+a1+a2+…+las=o-41+u2-3+4-5-35-243. (3)由4o+a1+2+…+a5=1,-o+1-2+…+45=-35, 得2(a1++s)=1-35 antastas121 (4)a0+1+2+…+5=1,-a0+M1-2+…+s=-35, 即Q0+2+04= 1+35-122. 2
解 导航 :(1)令x=1,得a0+a1+a2+…+a5 =1. (2)令x=-1,得-3 5=-a0+a1 -a2+a3 -a4+a5 . 由(2x-1)5 的通项 Tk+1=𝐂𝟓 𝒌 (-1)k ·2 5-k ·x 5-k 知 a1,a3,a5为负值, 因此|a0 |+|a1 |+|a2 |+…+|a5 |=a0 -a1+a2 -a3+a4 -a5 =3 5=243. (3)由a0+a1+a2+…+a5 =1,-a0+a1 -a2+…+a5 =-3 5 , 得2(a1+a3+a5 )=1-3 5 . 即 a1+a3+a5= 𝟏-𝟑 𝟓 𝟐 =-121. (4)a0+a1+a2+…+a5=1,-a0+a1-a2+…+a5=-3 5 , 即 a0+a2+a4= 𝟏+𝟑 𝟓 𝟐 =122

导航 (⑤)因为4是(2x-1)5展开式中x5的系数, 所以0=25=32. 又a0+a1+2+…+as=1, 所以1+2+u3+4+a5=-31. (6)因为(2.x-1)5=ur5++2x3+x2+a4+a5, 所以两边求导数得10(2x-1)4=5a4+4a13+32x2+2x+4 令x=1,得5a+4a1+32+2+a4-10
导航 (5)因为a0是(2x-1)5展开式中x 5的系数, 所以a0 =2 5=32. 又a0+a1+a2+…+a5 =1, 所以a1+a2+a3+a4+a5 =-31. (6)因为(2x-1)5=a0x 5+a1x 4+a2x 3+a3x 2+a4x+a5 , 所以两边求导数得10(2x-1)4=5a0x 4+4a1x 3+3a2x 2+2a3x+a4 . 令x=1,得5a0+4a1+3a2+2a3+a4 =10