
全程设计 第2课时 直线与圆的方程的应用
第2课时 直线与圆的方程的应用

素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练

导航 素养·目标定位 目标素养 知识概览 1.能用直线和圆的方 程解决一些简单的数 建系 学问题与实际问题 用坐标法解决平面几何问题的步骤 运算 2.体会用坐标法解决 翻译 平面几何问题的“三步 曲
导航 素养·目标定位 目 标 素 养 知 识 概 览 1.能用直线和圆的方 程解决一些简单的数 学问题与实际问题. 2.体会用坐标法解决 平面几何问题的“三步 曲”

导航 课前·基础认知 用坐标法解决几何问题的步骤 用坐标方法解决平面几何问题的“三步曲”: 第一步:建立 平面直角坐标系,用 表示问题中的几何元素,如点、直线、圆,将平面几何问题转 化为 第二步:通过代数运算,解决代数问题; 第三步:把 “翻译”成几何结论
导航 课前·基础认知 用坐标法解决几何问题的步骤 用坐标方法解决平面几何问题的“三步曲”: 第一步:建立 适当的 平面直角坐标系,用 坐标和方程 表示问题中的几何元素,如点、直线、圆,将平面几何问题转 化为 代数问题 ; 第二步:通过代数运算,解决代数问题; 第三步:把 代数运算结果 “翻译”成几何结论

导航 微思考用坐标法解决几何问题时,能随意建立坐标系吗? 提示:不能
导航 微思考 用坐标法解决几何问题时,能随意建立坐标系吗? 提示:不能

导航 课堂·重难突破 直线与圆的方程的实际应用 典例剖析 1.某圆拱桥的水面跨度20m,拱高4m.现有一船,宽10m,水面 以上高3m,这条船能否从桥下通过?
导航 课堂·重难突破 一 直线与圆的方程的实际应用 典例剖析 1.某圆拱桥的水面跨度20 m,拱高4 m.现有一船,宽10 m,水面 以上高3 m,这条船能否从桥下通过?

导 解:建立平面直角坐标系如图所示,使圆心C在y轴上依题意, 有A(←10,0),B(10,0),P(0,4),D(-5,0),E(5,0) 设这座圆拱桥的拱圆的方程是(k-02+0y-b)2=(0≤y≤4), (a+10)2+b2=r2, 于是有(a-10)2+b2=r2, a2+(b-4)2=r2. E B x 解此方程组,得=0,b=-10.5,=14.5. 所以这座圆拱桥的拱圆的方程是 x2+0y+10.5)2=14.52(0≤y≤4)
导航 解:建立平面直角坐标系如图所示,使圆心C在y轴上.依题意, 有A(-10,0),B(10,0),P(0,4),D(-5,0),E(5,0). 设这座圆拱桥的拱圆的方程是(x-a) 2+(y-b) 2=r2 (0≤y≤4), 于是有 (𝒂 + 𝟏𝟎) 𝟐 + 𝒃 𝟐 = 𝒓 𝟐 , (𝒂-𝟏𝟎) 𝟐 + 𝒃 𝟐 = 𝒓 𝟐 , 𝒂 𝟐 + (𝒃-𝟒) 𝟐 = 𝒓 𝟐 . 解此方程组,得a=0,b=-10.5,r=14.5. 所以这座圆拱桥的拱圆的方程是 x 2+(y+10.5)2=14.5 2 (0≤y≤4)

导航、 把点D的横坐标x=5代入上式,得≈3.1 由于船在水面以上高3m,3<3.1, 所以该船可以从桥下通过
导航 把点D的横坐标x=-5代入上式,得y≈3.1. 由于船在水面以上高3 m,3<3.1, 所以该船可以从桥下通过
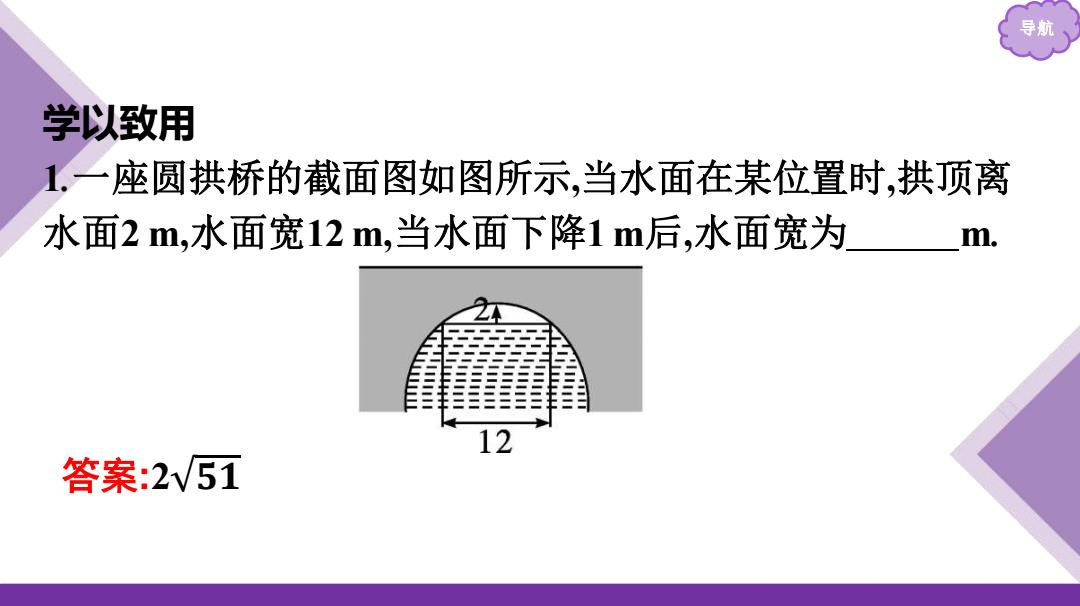
导航 学以致用 1.一座圆拱桥的截面图如图所示,当水面在某位置时,拱顶离 水面2m,水面宽12m,当水面下降1m后,水面宽为 m. 12 答案:2v51
导航 学以致用 1.一座圆拱桥的截面图如图所示,当水面在某位置时,拱顶离 水面2 m,水面宽12 m,当水面下降1 m后,水面宽为 m. 答案:2 𝟓𝟏

导 解析:如图,以圆拱桥桥洞顶点为坐标原点,以过 该顶,点的竖直直线为y轴,建立平面直角坐标系. 设圆心为C,圆的方程设为x2+(y+r)2=2,水面所 在弦的端点为A,B,则A(6,-2),将A(6,-2)代入圆的 方程,得=10,即圆的方程为x2+0y+10)2=100. 当水面下降1m后,可设点A',3)c>0),将A'K,-3)代入圆 的方程,得x0=V51,故当水面下降1m后,水面宽为2x0=2V51 m
导航 解析:如图,以圆拱桥桥洞顶点为坐标原点,以过 该顶点的竖直直线为y轴,建立平面直角坐标系. 设圆心为C,圆的方程设为x 2+(y+r) 2=r2 ,水面所 在弦的端点为A,B,则A(6,-2),将A(6,-2)代入圆的 方程,得r=10,即圆的方程为x 2+(y+10)2=100. 的方程,得 x0= 𝟓𝟏,故当水面下降 1 m 后,水面宽为 2x0=2 𝟓𝟏 m. 当水面下降1 m后,可设点A'(x0 ,-3)(x0>0),将A'(x0 ,-3)代入圆