
全程设计 6.1 分类加法计数原理与分步 乘法计数原理
6.1 分类加法计数原理与分步 乘法计数原理
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随 堂 训 练

导 素养·目标定位 目标素养 1.掌握分类加法计数原理与分步乘法计数原理的含义,理解两 个计数原理的区别与联系 2.正确理解“完成一件事情”的含义,能根据具体问题的特征, 选择“分类”或“分步”. 3.能利用两个计数原理解决一些简单的实际问题!
导航 目 标 素 养 1.掌握分类加法计数原理与分步乘法计数原理的含义,理解两 个计数原理的区别与联系. 2.正确理解“完成一件事情”的含义,能根据具体问题的特征, 选择“分类”或“分步” . 3.能利用两个计数原理解决一些简单的实际问题. 素养·目标定位
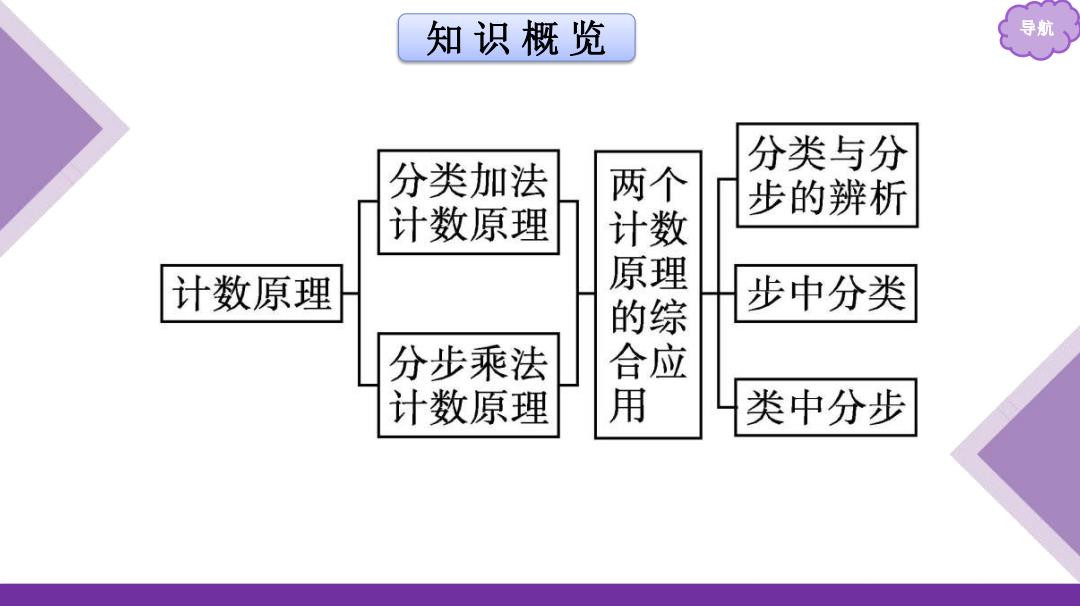
知识概览 导航 分类与分 分类加法 两个 步的辨析 计数原理 计数 计数原理 原 步中分类 分步乘法 的合 应 计数原理 类中分步
知 识 概 览 导航

导航 课前·基础认知 1.分类加法计数原理 完成一件事有两类不同方案,在第1类方案中有m种不同的 方法,在第2类方案中有种不同的方法,那么完成这件事共有 N- 种不同的方法
导航 1.分类加法计数原理 完成一件事有两类不同方案,在第1类方案中有m种不同的 方法,在第2类方案中有n种不同的方法,那么完成这件事共有 N= m+n 种不同的方法. 课前·基础认知

导期 微思考1如何理解分类加法计数原理中的完成一件事有两 类不同方案”? 提示:分类加法计数原理中的“完成一件事有两类不同方案”, 是指完成这件事的所有方法可以分为两类,即任何一类中的 任何一种方法都可以完成任务,两类中没有相同的方法,且完 成这件事的任何一种方法都在某一类中
导航 微思考1如何理解分类加法计数原理中的“完成一件事有两 类不同方案”? 提示:分类加法计数原理中的“完成一件事有两类不同方案”, 是指完成这件事的所有方法可以分为两类,即任何一类中的 任何一种方法都可以完成任务,两类中没有相同的方法,且完 成这件事的任何一种方法都在某一类中

导月 微训练1从A地到B地,可乘汽车、火车、轮船三种交通工具, 如果一天内汽车有3个班次,火车有4个班次轮船有2个班次, 那么一天内乘坐这三种交通工具从A地到B地,不同的方法种 数为() A.1+1+1=3 B.3+4+2=9 C.3X4×2=24 D.以上都不对 答案:B
导航 微训练1从A地到B地,可乘汽车、火车、轮船三种交通工具, 如果一天内汽车有3个班次,火车有4个班次,轮船有2个班次, 那么一天内乘坐这三种交通工具从A地到B地,不同的方法种 数为( ) A.1+1+1=3 B.3+4+2=9 C.3×4×2=24 D.以上都不对 答案:B

导航 解析:分三类:第一类,乘汽车,从3个班次中选1个班次有3种 方法;第二类,乘火车,从4个班次中选1个班次有4种方法;第三 类,乘轮船,从2个班次中选1个班次有2种方法.根据分类加法 计数原理,共有3+4+2=9种不同的方法
导航 解析:分三类:第一类,乘汽车,从3个班次中选1个班次有3种 方法;第二类,乘火车,从4个班次中选1个班次有4种方法;第三 类,乘轮船,从2个班次中选1个班次有2种方法.根据分类加法 计数原理,共有3+4+2=9种不同的方法

导航 2.分步乘法计数原理 完成一件事需要两个步骤,做第1步有m种不同的方法,做第2 步有种不同的方法,那么完成这件事共有N= 种不 同的方法
导航 2.分步乘法计数原理 完成一件事需要两个步骤,做第1步有m种不同的方法,做第2 步有n种不同的方法,那么完成这件事共有N= m×n 种不 同的方法

微思考2(1)如何理解分步乘法计数原理中的“完成一件事需 要两个步骤”? 提示:分步乘法计数原理中的“完成一件事需要两个步骤”, 是指完成这件事的任何一种方法,都需要分成两个步骤首先 在每一个步骤中任取一种方法,然后相继完成这两个步骤就 能完成这件事,即各个步骤是相互依存的,每个步骤都要做完 才能完成这件事
导航 微思考2(1)如何理解分步乘法计数原理中的“完成一件事需 要两个步骤”? 提示:分步乘法计数原理中的“完成一件事需要两个步骤”, 是指完成这件事的任何一种方法,都需要分成两个步骤.首先 在每一个步骤中任取一种方法,然后相继完成这两个步骤就 能完成这件事,即各个步骤是相互依存的,每个步骤都要做完 才能完成这件事