
全程设计 8.1 成对数据的统计相关性
8.1 成对数据的统计相关性
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
课堂·重难突破 素养·目标定位 课前·基础认知 随 堂 训 练

导航 素养·目标定位 目标素养 1.了解变量间的相关关系,会画散点图. 2.根据散点图和样本相关系数,能判断两个变量是否具有相 关关系
导航 目 标 素 养 1.了解变量间的相关关系,会画散点图. 2.根据散点图和样本相关系数r,能判断两个变量是否具有相 关关系. 素养·目标定位
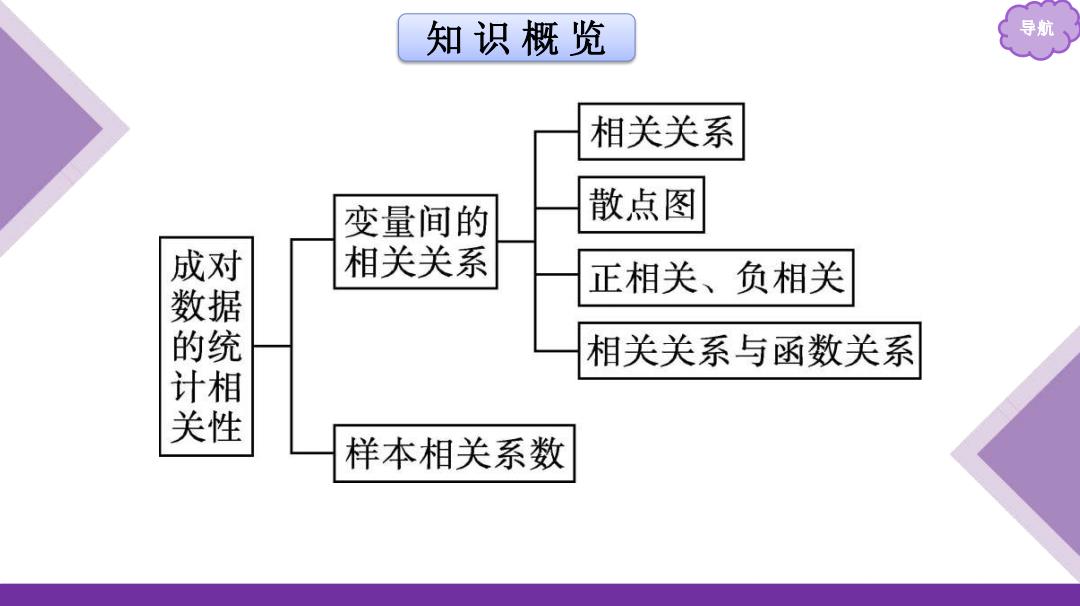
知识概览 导航 相关关系 变量间的 散点图 成对 相关关系 正相关、负相关 数据 的统 相关关系与函数关系 计相 关性 样本相关系数
知 识 概 览 导航

导航 课前·基础认知 1.变量的相关关系 两个变量有关系,但又没有确切到可由其中的一个去精确地 决定另一个的程度,这种关系称为
导航 1.变量的相关关系 两个变量有关系,但又没有确切到可由其中的一个去精确地 决定另一个的程度,这种关系称为 相关关系 . 课前·基础认知

导 微思考两个变量间的关系有几类? 提示:两个变量间的关系分为三类:第一类是确定性的函数 关系,如正方形边长与面积的关系;第二类是变量间确实存在 关系,但又不具备函数关系所要求的确定性,它们的关系是带 有随机性的,这种关系就是相关关系,如某名同学的“物理成绩” 与“数学成绩”之间的关系;第三类是不相关,即两变量没有任 何关系
导航 微思考两个变量间的关系有几类? 提示:两个变量间的关系分为三类:第一类是确定性的函数 关系,如正方形边长与面积的关系;第二类是变量间确实存在 关系,但又不具备函数关系所要求的确定性,它们的关系是带 有随机性的,这种关系就是相关关系,如某名同学的“物理成绩” 与“数学成绩”之间的关系;第三类是不相关,即两变量没有任 何关系

导航 微训练1(1)下列变量之间的关系是相关关系的是( A.出租车费与行驶的里程 B.房屋面积与房屋价格 C.身高与体重 D.铁块的体积与质量 答案:C 解析:A,B,D中的两个变量是函数关系
导航 微训练1(1)下列变量之间的关系是相关关系的是( ) A.出租车费与行驶的里程 B.房屋面积与房屋价格 C.身高与体重 D.铁块的体积与质量 答案:C 解析:A,B,D中的两个变量都是函数关系

导航 2)下列变量之间的关系是相关关系的是( A.正方体的表面积与体积 B.光照时间与果树产量 C.匀速行驶车辆的行驶距离与时间 D.中国足球队的比赛成绩与中国乒乓球队的比赛成绩 答案:B 解析:A,C是函数关系,D无相关关系
导航 (2)下列变量之间的关系是相关关系的是( ) A.正方体的表面积与体积 B.光照时间与果树产量 C.匀速行驶车辆的行驶距离与时间 D.中国足球队的比赛成绩与中国乒乓球队的比赛成绩 答案:B 解析:A,C是函数关系,D无相关关系

导航 2.散点图、线性相同 1)散点图 每个编号下的成对样本数据都可用直角坐标系中的点表示 出来,由这些点组成统计图,我们把这样的统计图叫做
导航 2.散点图、线性相同 (1)散点图 每个编号下的成对样本数据都可用直角坐标系中的点表示 出来,由这些点组成统计图,我们把这样的统计图叫做 散点图

(2)正相关与负相关 如果从整体上看,当一个变量的值增加时,另一个变量的相 应值也呈现增加的趋势,我们就称这两个变量 ;如 果当一个变量的值增加时,另一个变量的相应值呈现减少的 趋势,则称这两个变量 (3)线性相关 一般地,如果两个变量的取值呈现正相关或负相关,而且散 点落在一条直线附近,我们就称这两个变量
导航 (2)正相关与负相关 如果从整体上看,当一个变量的值增加时,另一个变量的相 应值也呈现增加的趋势,我们就称这两个变量 正相关 ;如 果当一个变量的值增加时,另一个变量的相应值呈现减少的 趋势,则称这两个变量 负相关 . (3)线性相关 一般地,如果两个变量的取值呈现正相关或负相关,而且散 点落在一条直线附近,我们就称这两个变量 线性相关