
全程设计 8.3 列联表与独立性检验
8.3 列联表与独立性检验
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随 堂 训 练

导航 素养·目标定位 目标素养 1.了解分类变量、2×2列联表、随机变量的意义, 2.了解独立性检验的基本思想方法 3.了解两个分类变量的独立性检验的应用
导航 目 标 素 养 1.了解分类变量、2×2列联表、随机变量χ 2的意义. 2.了解独立性检验的基本思想方法. 3.了解两个分类变量的独立性检验的应用. 素养·目标定位
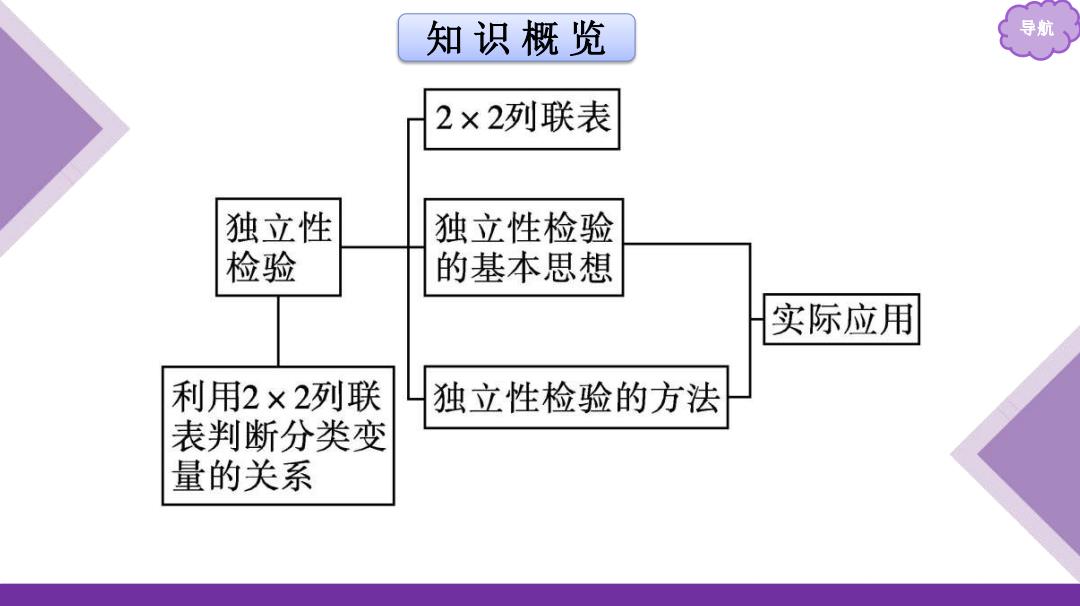
知识概览 导航 2×2列联表 独立性 独立性检验 检验 的基本思想 实际应用 利用2×2列联 独立性检验的方法 表判断分类变 量的关系
知 识 概 览 导航

导航 课前·基础认知 1.分类变量与列联表 (1)分类变量 我们经常会使用一种特殊的随机变量,以区别不同的现象或 性质,这类随机变量称为 .分类变量的取值可以 用实数表示
导航 1.分类变量与列联表 (1)分类变量 我们经常会使用一种特殊的随机变量,以区别不同的现象或 性质,这类随机变量称为 分类变量 .分类变量的取值可以 用实数表示. 课前·基础认知

(2)列联表 导航 按研究问题的需要,将数据分类统计,并做成表格加以保存 我们将下表这种形式的数据统计表称为 2×2列联表给出了成对分类变量数据的交叉分类频数 Y X 合计 Y=0 Y=1 X=0 a b a+b X=1 c d c+d 合计 a+c b+d n=a+b+c+d
导航 (2)列联表 按研究问题的需要,将数据分类统计,并做成表格加以保存. 我们将下表这种形式的数据统计表称为 2×2列联表 . 2×2列联表给出了成对分类变量数据的交叉分类频数. X Y 合计 Y=0 Y=1 X=0 a b a+b X=1 c d c+d 合计 a+c b+d n=a+b+c+d

导 2.独立性检验 ()利用的取值推断分类变量X和Y是否独立的方法称为 ,读作“ ”,简称独立性检 验 (2)独立性检验公式 n(ad-bc)2 a+be+da+ch+而(其中m=a+h+c+0
导航 2.独立性检验 (1)利用χ 2的取值推断分类变量X和Y是否独立的方法称为 χ 2独立性检验 ,读作“ 卡方独立性检验 ”,简称独立性检 验. (2)独立性检验公式 χ 2 = 𝒏(𝒂𝒅-𝒃𝒄) 𝟐 (𝒂+𝒃)(𝒄+𝒅)(𝒂+𝒄)(𝒃+𝒅) .(其中 n=a+b+c+d)
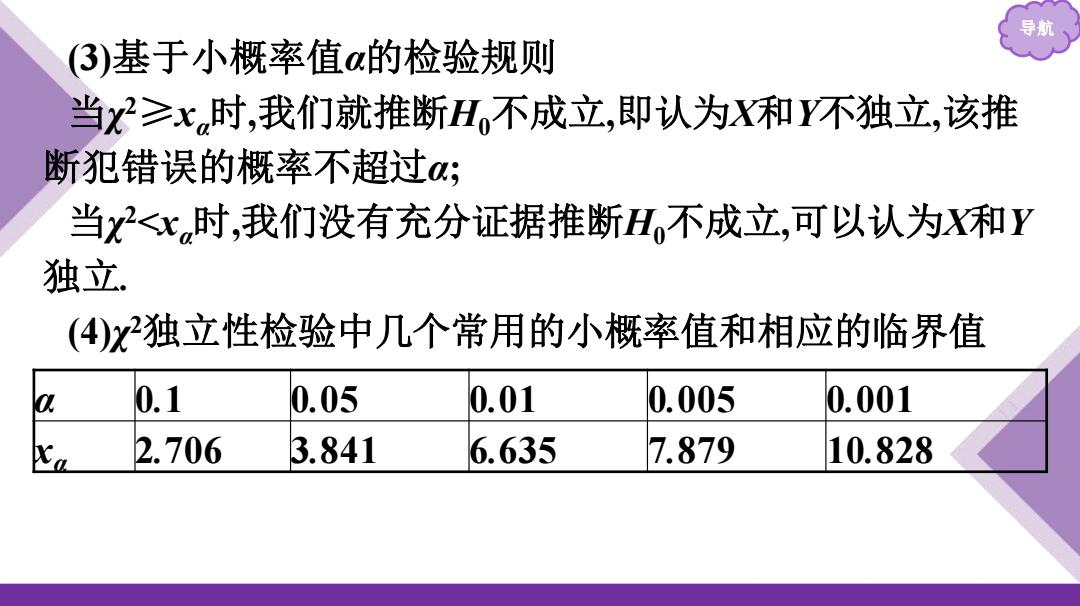
导月 3)基于小概率值的检验规则 当x≥x时,我们就推断H,不成立,即认为X和Y不独立,该推 断犯错误的概率不超过a; 当2<x时,我们没有充分证据推断H不成立,可以认为X和Y 独立 (4)x独立性检验中几个常用的小概率值和相应的临界值 0.1 0.05 0.01 0.005 0.001 2.706 3.841 6.635 7.879 10.828
导航 (3)基于小概率值α的检验规则 当χ 2≥xα时,我们就推断H0不成立,即认为X和Y不独立,该推 断犯错误的概率不超过α; 当χ 2<xα时,我们没有充分证据推断H0不成立,可以认为X和Y 独立. (4)χ 2独立性检验中几个常用的小概率值和相应的临界值 α 0.1 0.05 0.01 0.005 0.001 xα 2.706 3.841 6.635 7.879 10.828

微思考独立性检验的基本思想与反证法的思想有何相似之处?导航 提示: 反证法 假设检验 要证明结论A 要确认“两个变量有关系” 在A不成立的前提下进 假设该结论不成立,即假设结论“两个变 行推理 量没有关系”成立,在该假设下计算x2 推出矛盾,意味着结论A 由观测数据计算得到的很大,则在一定 成立 可信程度上说明假设不合理 没有找到矛盾,不能对A 根据随机变量的含义,可以通过的大 下任何结论,即反证不成小来判断“两个变量有关系”这一结论成 立 立有多大把握
微思考独立性检验的基本思想与反证法的思想有何相似之处 导航 ? 提示: 反证法 假设检验 要证明结论A 要确认“两个变量有关系” 在A不成立的前提下进 行推理 假设该结论不成立,即假设结论“两个变 量没有关系”成立,在该假设下计算χ 2 推出矛盾,意味着结论A 成立 由观测数据计算得到的χ 2很大,则在一定 可信程度上说明假设不合理 没有找到矛盾,不能对A 下任何结论,即反证不成 立 根据随机变量χ 2的含义,可以通过χ 2的大 小来判断“两个变量有关系”这一结论成 立有多大把握

导航 微训练下面是一个2×2列联表: 则表中4,b处的值分别为( Y 合计 A.94,96 B.52,50 Y=0 Y=1 C.52,54 D.54,52 X=0 L 21 73 答案:C X=1 2 25 27 解析:=73-21=52,b=100-46=54, 合计 b 46 100
导航 微训练下面是一个2×2列联表: 则表中a,b处的值分别为( ) A.94,96 B.52,50 C.52,54 D.54,52 答案:C 解析:a=73-21=52,b=100-46=54. X Y 合计 Y=0 Y=1 X=0 a 21 73 X=1 2 25 27 合计 b 46 100