
全程设计 章末核心素养整合
章末核心素养整合

知识体系构建 专题归纳突破
知识体系构建 专题归纳突破
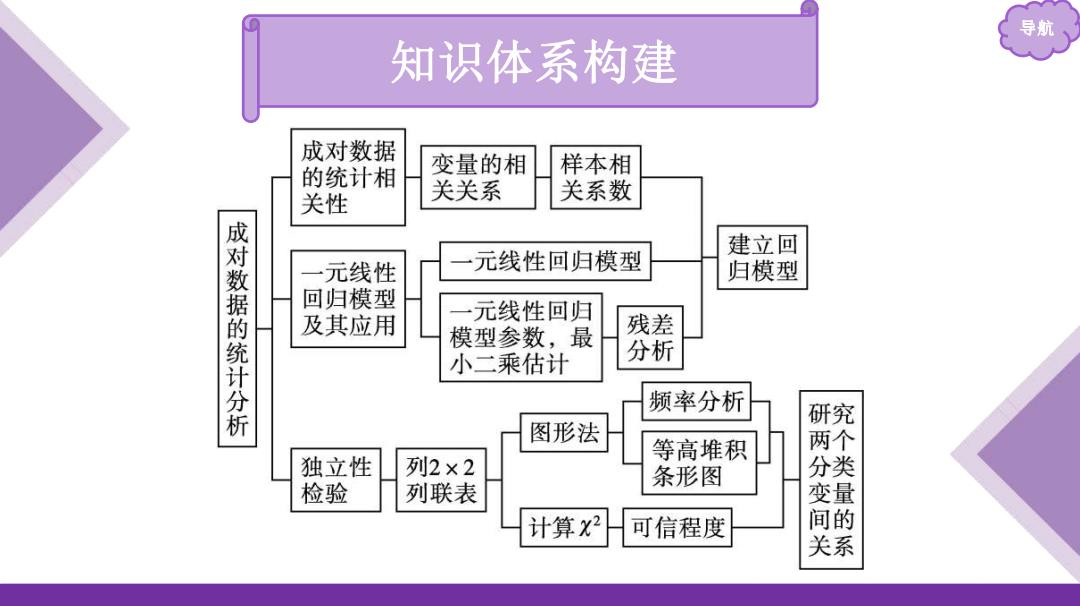
导航 知识体系构建 成对数据 的统计相 变量的相 样本相 关性 关关系 关系数 建立回 成对数据的统计分析 元线性 元线性回归模型 归模型 回归模型 元线性回归 及其应用 模型参数,最 残差 小二乘估计 分析 频率分析 研究 图形法 等高堆积 两个 独立性 列2×2 条形图 分类 检验 列联表 变量 计算2 可信程度 间的 关系
导航 知识体系构建

导航 专题归纳突破 专题一成对数据的统计分析 根据两个变量的一组观测值,可以画出散点图或利用样本相 关系数,判断两个变量是否具有线性相关关系,若具有相关关 系,则可得出经验回归方程
导航 专题一 成对数据的统计分析 根据两个变量的一组观测值,可以画出散点图或利用样本相 关系数r,判断两个变量是否具有线性相关关系,若具有相关关 系,则可得出经验回归方程. 专题归纳突破

导航 利用公式求经验回归方程时应注意以下几点: (四求b时,利用公式b=-0 ,先求出x= 名x2 ctx2+x+t比万=yty2ty+…+n以再由a=歹-b求a的值, 并写出经验回归方程
导航 利用公式求经验回归方程时应注意以下几点: (1)求𝒃 ^ 时,利用公式𝐛 ^ = ∑ 𝒊=𝟏 𝒏 (𝒙𝒊 -𝒙)(𝒚𝒊 -𝒚) ∑ 𝒊=𝟏 𝒏 (𝒙𝒊 -𝒙) 𝟐 ,先求出𝒙 = 𝟏 𝒏 (x1+x2+x3+…+xn),𝒚 = 𝟏 𝒏 (y1+y2+y3+…+yn).再由𝒂 ^ = 𝒚 − 𝒃 ^ 𝒙求𝒂 ^ 的值, 并写出经验回归方程

导航 2)经验回归直线一定经过样本点的中心(,习), (3)经验回归方程中的截距α和斜率b都是通过样本估计得来的,存 在误差,这种误差可能导致预测结果的偏差 (4)经验回归方程y=a+x中的b表示x每增加1个单位时预测 值y的平均变化量,而α表示预测值y不随x的变化而变化的部分
导航 (2)经验回归直线一定经过样本点的中心(𝒙, 𝒚). (3)经验回归方程中的截距𝒂 ^ 和斜率𝒃 ^ 都是通过样本估计得来的,存 在误差,这种误差可能导致预测结果的偏差. (4)经验回归方程𝒚 ^ = 𝒂 ^ + 𝒃 ^ x 中的𝒃 ^ 表示 x 每增加 1 个单位时预测 值𝒚 ^ 的平均变化量,而𝒂 ^ 表示预测值𝒚 ^ 不随 x 的变化而变化的部分

导 (⑤)对于建立的回归模型,我们必须对模型的拟合效果进行 分析,也就是对利用回归模型解决实际问题的效果进行评价: 一方面可以对比残差或残差平方和的大小,同时观察残差图, 进行残差分析;另一方面也可以研究数据的2(样本相关系数 ).对模型拟合效果的分析能够帮助我们利用最优化的模型来 解决实际问题
导航 (5)对于建立的回归模型,我们必须对模型的拟合效果进行 分析,也就是对利用回归模型解决实际问题的效果进行评价. 一方面可以对比残差或残差平方和的大小,同时观察残差图, 进行残差分析;另一方面也可以研究数据的R2 (样本相关系数 r).对模型拟合效果的分析能够帮助我们利用最优化的模型来 解决实际问题
导航 【典型例题1】对于x与y有如下观测数据: 18 25 30 39 41 42 49 52 5 6 7 8 8 9 10 (1)作出散点图; (2)对x与y作回归分析; 3)求出y关于x的经验回归方程; (4)根据经验回归方程,预测当=60时y的值
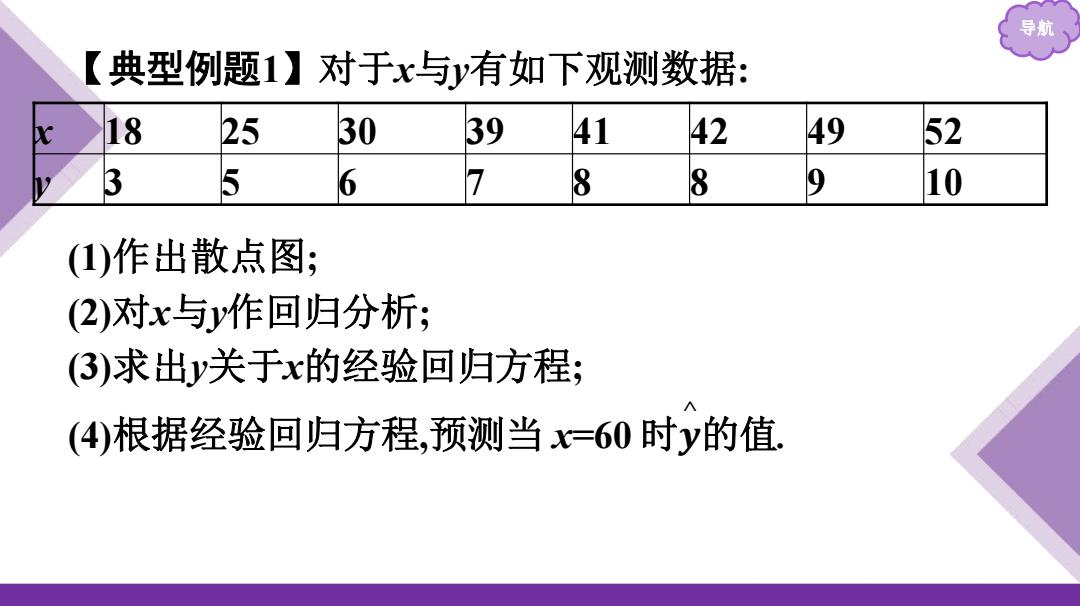
导航 【典型例题1】对于x与y有如下观测数据: x 18 25 30 39 41 42 49 52 y 3 5 6 7 8 8 9 10 (1)作出散点图; (2)对x与y作回归分析; (3)求出y关于x的经验回归方程; (4)根据经验回归方程,预测当 x=60 时𝒚 ^ 的值
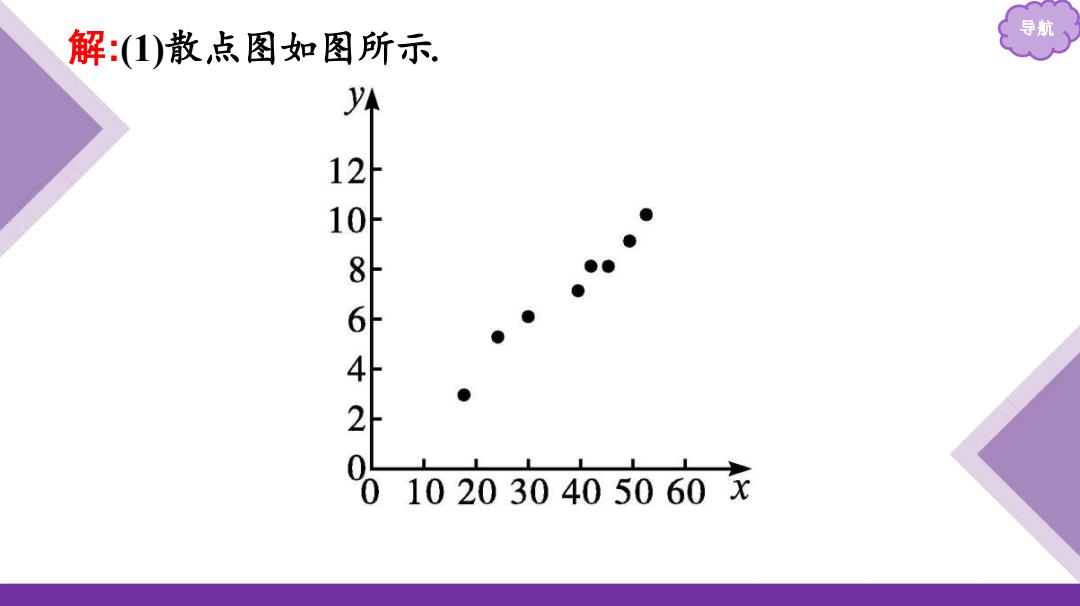
解:1)散点图如图所示 导航 个 20 8642 0 102030405060x
导航 解 :(1)散点图如图所示

(2)作相关性检验: 导航 = (18+25+30+39+41+42+49+52)296-37, 8 y=。×(3+5+6+7+8+8+9+10)=7, 8 8 182+252+3024392+412+422+492+522 8 7-32452462+72+82+82+924102-428. 8 xy=18×3+25×5+30×6+39×7+41×8+42×8+49×9+52×10=2257, i=1 含0r8x-2257-8×37×7=185
导航 (2)作相关性检验: 𝐱 = 𝟏 𝟖 ×(18+25+30+39+41+42+49+52)= 𝟐𝟗𝟔 𝟖 =37, 𝐲 = 𝟏 𝟖 ×(3+5+6+7+8+8+9+10)=7, ∑ 𝐢=𝟏 𝟖 𝒙𝒊 𝟐 =182 +252 +302 +392 +412 +422 +492 +522 =11 920, ∑ 𝒊=𝟏 𝟖 𝒚𝒊 𝟐 =3 2 +5 2 +6 2 +7 2 +8 2 +8 2 +9 2 +102 =428, ∑ 𝒊=𝟏 𝟖 xiyi=18×3+25×5+30×6+39×7+41×8+42×8+49×9+52×10=2 257, ∑ 𝒊=𝟏 𝟖 xiyi-8𝒙 𝒚=2 257-8×37×7=185