
全程设计 6.2 排列与组合 第2课时 排列的应用
6.2 排列与组合 第2课时 排列的应用
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随 堂 训 练

导航 素养·目标定位 目标素养 1.进一步加深对排列定义的理解 2.掌握几种有限制条件的排列,能应用排列数公式解决简单的 实际问题
导航 目 标 素 养 1.进一步加深对排列定义的理解. 2.掌握几种有限制条件的排列,能应用排列数公式解决简单的 实际问题. 素养·目标定位
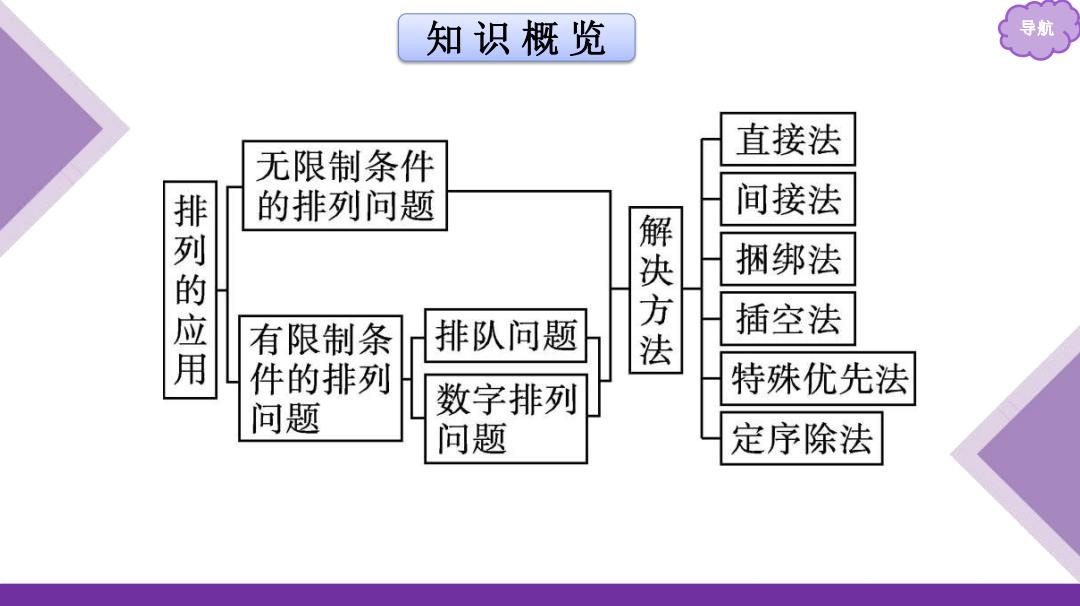
知识概览 导航 直接法 无限制条件 的排列问题 间接法 排列的应用 捆绑法 有限制条 排队问题 决方法 插空法 件的排列 特殊优先法 问题 数字排列 问题 定序除法
知 识 概 览 导航

导航 课前·基础认知 1.排列数公式 A吸=mr-l-2…-1)∈N且m≤W A2=n(n-1)(n-2)×…×2×1=n:(叫做n的阶乘) 另外,我们规定0!=1
导航 课前·基础认知 1.排列数公式 另外,我们规定0!=1. 𝐀𝒏 𝒎=n(n-1)(n-2)…(n-m+1)= 𝒏! (𝒏-𝒎)! (n,m∈N * ,且 m≤n) 𝐀𝒏 𝒏 =n(n-1)(n-2)×…×2×1=n!(叫做 n 的阶乘)
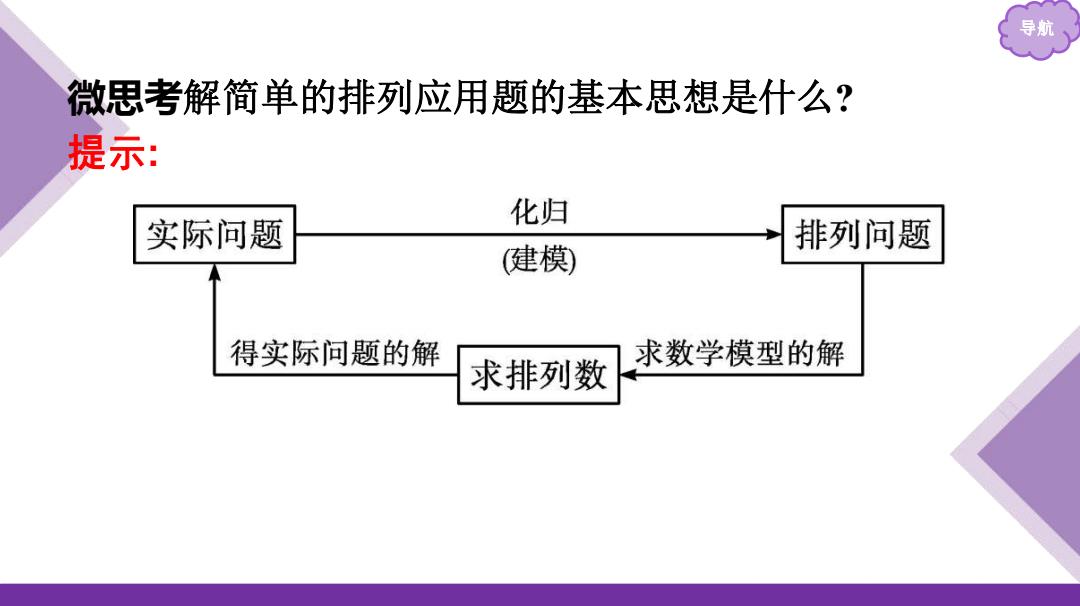
导航 微思考解简单的排列应用题的基本思想是什么? 提示: 化归 实际问题 排列问题 建模) 得实际问题的解 求数学模型的解 求排列数
导航 微思考解简单的排列应用题的基本思想是什么? 提示:

2.解决排列应用题的常用方法 ()位置分析法:以位置为主,特殊(受限)的位置优先考虑.有 两个以上的约束条件时,往往根据其中的一个条件分类处理。 (2)元素分析法:以元素为主,先满足特殊(受限)元素的要求, 再处理其他元素若有两个以上的约束条件,往往考虑一个元 素的同时,兼顾其他元素。 (3)间接法:也叫排异法,直接考虑时情况较多、不易计算,但 其对立面情况较少,相对来讲比直接解答简捷,可以先求出对 立面,再从总体情况中减除
导航 2.解决排列应用题的常用方法 (1)位置分析法:以位置为主,特殊(受限)的位置优先考虑.有 两个以上的约束条件时,往往根据其中的一个条件分类处理. (2)元素分析法:以元素为主,先满足特殊(受限)元素的要求, 再处理其他元素.若有两个以上的约束条件,往往考虑一个元 素的同时,兼顾其他元素. (3)间接法:也叫排异法,直接考虑时情况较多、不易计算,但 其对立面情况较少,相对来讲比直接解答简捷,可以先求出对 立面,再从总体情况中减除

〔4)插空法:首先把无限制的元素排好,然后将不能相邻的元 素插入排好的元素形成的空中要注意无限制条件的元素的 排列数及所形成的空的个数,此方法适用于“不相邻”问题的 排列. (⑤)捆绑法:把要求捆绑在一起的相邻元素看成一个整体,与 其他元素进行排列,同时需要考虑捆绑元素的内部排序.此法 适用于“相邻”问题的排列
导航 (4)插空法:首先把无限制的元素排好,然后将不能相邻的元 素插入排好的元素形成的空中.要注意无限制条件的元素的 排列数及所形成的空的个数,此方法适用于“不相邻”问题的 排列. (5)捆绑法:把要求捆绑在一起的相邻元素看成一个整体,与 其他元素进行排列,同时需要考虑捆绑元素的内部排序.此法 适用于“相邻”问题的排列

导 微训川练(1)用数字1,2,3,4,5组成的无重复数字的四位偶数的 个数为 答案:48 解析:先从2,4中取一个数作为个位数字,有2种取法;再从其 余四个数中取出三个数排在前三位,有A3种排法.由分步乘法计 数原理知,这样的四位偶数共有2×A=48个
导航 微训练(1)用数字1,2,3,4,5组成的无重复数字的四位偶数的 个数为 . 答案:48 解 析:先从 2,4 中取一个数作为个位数字,有 2种取法;再从其 余四个数中取出三个数排在前三位,有𝐀𝟒 𝟑 种排法.由分步乘法计 数原理知,这样的四位偶数共有 2×𝐀𝟒 𝟑 =48 个

导 (2)A,B,C,D,E五人并排站成一排,如果A,B必须相邻且B在A 的右边,那么不同的排法种数有 种. 答案:24 解析:把A,B视为一个整体,且B固定在A的右边,则本题相当 于4人的全排列,不同的排法共A4=24种
导航 (2)A,B,C,D,E五人并排站成一排,如果A,B必须相邻且B在A 的右边,那么不同的排法种数有 种. 答案:24 解析:把A,B视为一个整体,且B固定在A的右边,则本题相当 于4人的全排列,不同的排法共 𝐀𝟒 =24种. 𝟒