
全程设计 2.2.2 直线的两点式方程
2.2.2 直线的两点式方程
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
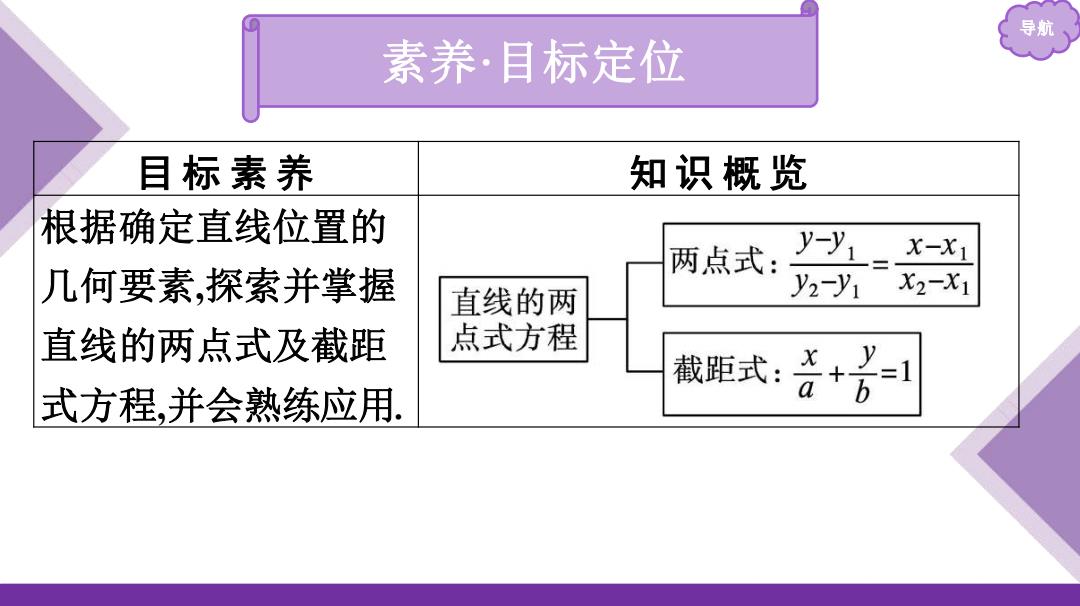
导航 素养·目标定位 目标素养 知识概览 根据确定直线位置的 两点式: y-y1= x-X1 几何要素,探索并掌握 直线的两 y2-y1 X2-x1 直线的两点式及截距 点式方程 式方程,并会熟练应用 截距式:言+
导航 素养·目标定位 目 标 素 养 知 识 概 览 根据确定直线位置的 几何要素,探索并掌握 直线的两点式及截距 式方程,并会熟练应用

导航 课前·基础认知 直线的两点式与截距式方程 名称 两点式 截距式 直线过点P1(c1y)和 直线在x轴上截距为a, 已知条件 P2飞2y2,其中xx2y12 在y轴上截距为b 示意图
导航 课前·基础认知 直线的两点式与截距式方程 名称 两点式 截距式 已知条件 直线过点P1 (x1 ,y1 )和 P2 (x2 ,y2 ),其中x1≠x2 ,y1≠y2 直线在x轴上截距为a, 在y轴上截距为b 示意图

导航、 名称 两点式 截距式 y-y1 X-X1 方程 y2-y1 X2-X1 + 适用条件斜率存在,且不为0 呋0,且b0
导航 名称 两点式 截距式 方程 ____________ ______________ 适用条件 斜率存在,且不为0 a≠0,且b≠0 𝐲-𝐲𝟏 𝐲𝟐-𝐲𝟏 = 𝐱-𝐱𝟏 𝐱𝟐-𝐱𝟏 𝐱 𝐚 + 𝐲 𝐛 =1

微思考(1)过点(1,3)和(1,5)的直线能用两点式表示吗?为什么? 过点(2,3),(5,3)的直线呢? (2)截距式方程能否表示过原点的直线? 提示:1)不能,因为1-1=0,而0不能作分母.同理过点(2,3),(5,3) 的直线也不能用两点式表示 (2)不能,在截距式方程中,b≠0,即有两个非零截距,故截距式 方程不能表示过原点的直线
导航 微思考 (1)过点(1,3)和(1,5)的直线能用两点式表示吗?为什么? 过点(2,3),(5,3)的直线呢? (2)截距式方程能否表示过原点的直线? 提示:(1)不能,因为1-1=0,而0不能作分母.同理过点(2,3),(5,3) 的直线也不能用两点式表示. (2)不能,在截距式方程中,ab≠0,即有两个非零截距,故截距式 方程不能表示过原点的直线

导航 微训练(1)直线3x-2y=4的截距式方程是( A. 4 -4 2 3x y-1 D 4 3 答案:D 解析:求直线方程的截距式,必须把方程化为 +言=1的形式, 即右边为1,左边是和的形式
导航 微训练(1)直线3x-2y=4的截距式方程是( ) A. 𝟑𝒙 𝟒 − 𝒚 𝟐 =1 B. 𝒙 𝟏 𝟑 − 𝒚 𝟏 𝟐 =4 C. 𝟑𝒙 𝟒 − 𝒚 -𝟐 =1 D. 𝒙 𝟒 𝟑 + 𝒚 -𝟐 =1 答案:D 解析:求直线方程的截距式,必须把方程化为 =1的形式, 即右边为1,左边是和的形式. 𝒙 𝒂 + 𝒚 𝒃

导航 (2)过P1(2,0),P2(0,3)两点的直线方程是( A写+0 B =1 2 D y-1 答案:C 解析:由截距式得所求直线的方程为 + =1
导航 (2)过P1 (2,0),P2 (0,3)两点的直线方程是( ) A. 𝒙 𝟑 + 𝒚 𝟐 =0 B. 𝒙 𝟑 − 𝒚 𝟐 =1 C. 𝒙 𝟐 + 𝒚 𝟑 =1 D. 𝒙 𝟐 − 𝒚 𝟑 =1 答案:C 解析:由截距式得所求直线的方程为 =1. 𝒙 𝟐 + 𝒚 𝟑

导航 课堂·重难突破 直线的两点式方程 典例剖析 1.已知三角形的顶点是A(1,3),B(-2,-1),C(1,-1),求这个三角形 三边所在直线的方程 y 3 解:直线AB过A(1,3),B(-2,-1),其两点式方程 为y3 x-1 ,整理得直线AB的方程为 -1-3--2-1 4x-3y+5=0.直线AC垂直于x轴,其方程为x=1. -2 直线BC平行于x轴,其方程为y=-1
导航 课堂·重难突破 一 直线的两点式方程 典例剖析 1.已知三角形的顶点是A(1,3),B(-2,-1),C(1,-1),求这个三角形 三边所在直线的方程. 解:直线AB过A(1,3),B(-2,-1),其两点式方程 为 ,整理得直线AB的方程为 4x-3y+5=0.直线AC垂直于x轴,其方程为x=1. 直线BC平行于x轴,其方程为y=-1. 𝒚-𝟑 -𝟏-𝟑 = 𝒙-𝟏 -𝟐-𝟏

导航 规律总结利用两点式求直线方程的策略: 当已知两点坐标,求过这两点的直线方程时,先要判断是否满 足两点式方程的适用条件,若满足即可考虑用两点式求方程. 在斜率存在的情况下,也可以先应用斜率公式求出斜率,再用 点斜式写方程
导航 规律总结 利用两点式求直线方程的策略: 当已知两点坐标,求过这两点的直线方程时,先要判断是否满 足两点式方程的适用条件,若满足即可考虑用两点式求方程. 在斜率存在的情况下,也可以先应用斜率公式求出斜率,再用 点斜式写方程