
全程设计 2.2.3 直线的一般式方程
2.2.3 直线的一般式方程
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
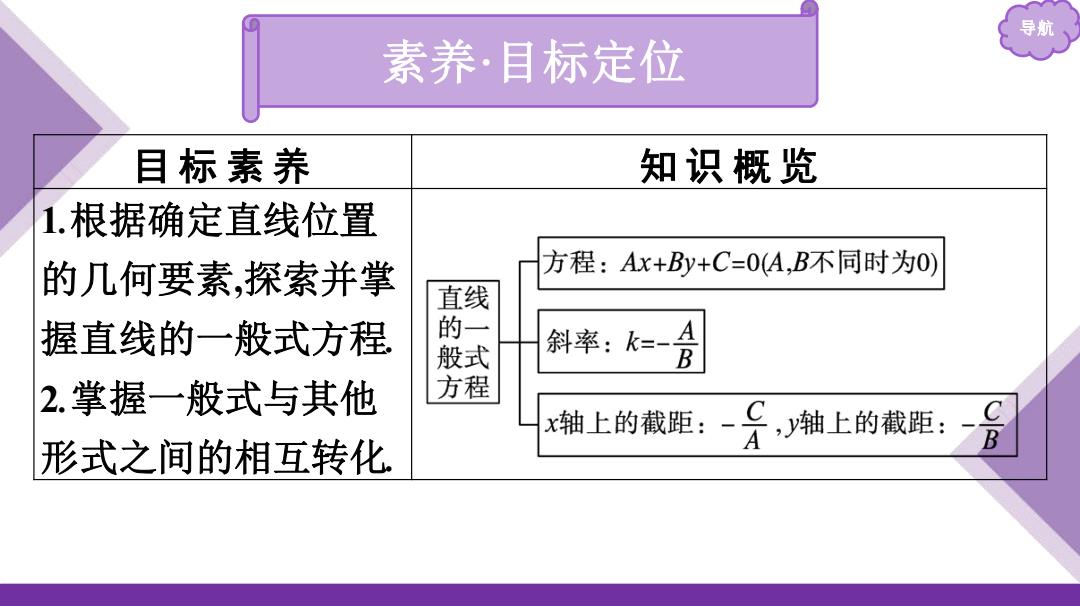
导航 素养·目标定位 目标素养 知识概览 1.根据确定直线位置 的几何要素,探索并掌 方程:Ax+By+C=0(A,B不同时为0) 直线 握直线的一般式方程 的一 般式 斜率:k=- 2.掌握一般式与其他 方程 轴上的截距:-牙,潮上的截距:一吕 形式之间的相互转化
导航 素养·目标定位 目 标 素 养 知 识 概 览 1.根据确定直线位置 的几何要素,探索并掌 握直线的一般式方程. 2.掌握一般式与其他 形式之间的相互转化

导航 课前·基础认知 1.直线的一般式方程 我们把关于x,y的二元一次方程 (其中A,B不 同时为0)叫做直线的一般式方程,简称一般式
导航 课前·基础认知 1.直线的一般式方程 我们把关于x,y的二元一次方程 Ax+By+C=0 (其中A,B不 同时为0)叫做直线的一般式方程,简称一般式
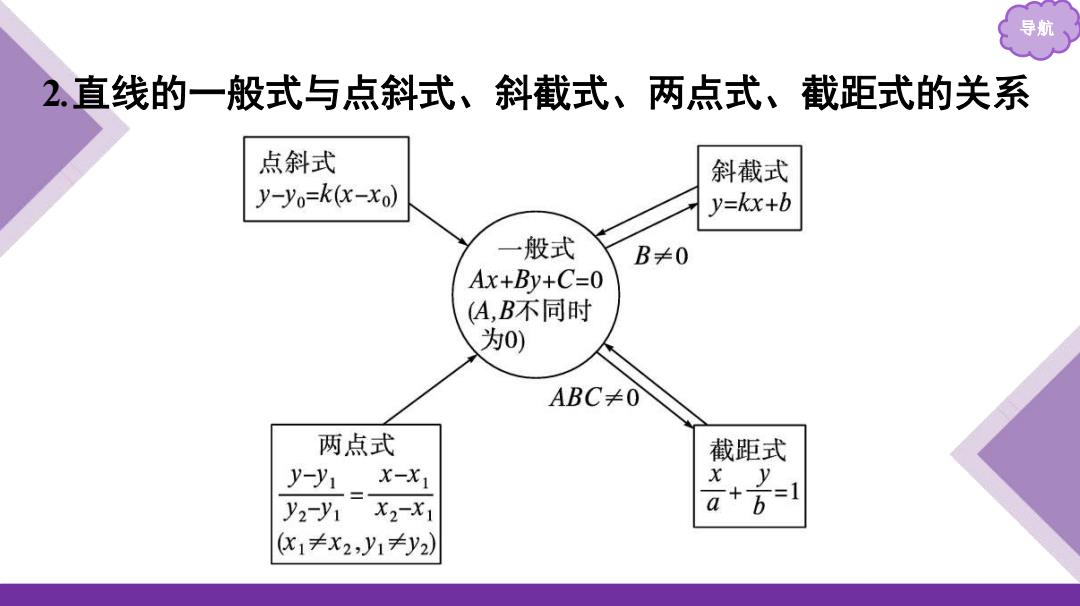
导航 2.直线的一般式与点斜式、斜截式、两点式、截距式的关系 点斜式 斜截式 y-yo=k(x-xo) y=kx+b 般式 B≠0 Ax+By+C=0 (A,B不同时 为0) ABC≠0 两点式 截距式 y-y1 x-X1 y2-y1 X2-X1 a (x1≠x2,y1≠y2)
导航 2.直线的一般式与点斜式、斜截式、两点式、截距式的关系

导航 形式 方程 适用条件 点斜式 V-Yo=k(x-xo) 表示斜率 的直线 斜截式 y=kx+b 表示斜率存在的直线 两点式 y-y1= X-X1 斜率存在,且不为 y2-y1 X2-X1 截距式 + 一般式 Ax+By+C-0 均适用
导航 形式 方程 适用条件 点斜式 y-y0=k(x-x0 ) 表示斜率 存在 的直线 斜截式 y=kx+b 表示斜率存在的直线 两点式 斜率存在,且不为 0 截距式 a≠0,且b≠0 一般式 Ax+By+C=0 均适用 𝐲-𝐲𝟏 𝐲𝟐-𝐲𝟏 = 𝐱-𝐱𝟏 𝐱𝟐-𝐱𝟏 𝐱 𝐚 + 𝐲 𝐛 =1

导 微思考(1)关于x,y的二元一次方程Ax+By+C=0(A,B不同时为0) 一定表示直线吗? (2)当A=0,或B=0,或C=0时,方程Ax+By+C=0分别表示什么样 的直线? 提示:(少一定 20若A10,则表示与轴垂直的一条直线 ②若B-0,则,=牙表示与x轴垂直的一条直线. ③若C=0,则A+By=0,表示过原点的一条直线
导航 微思考(1)关于x,y的二元一次方程Ax+By+C=0(A,B不同时为0) 一定表示直线吗? (2)当A=0,或B=0,或C=0时,方程Ax+By+C=0分别表示什么样 的直线? 提示:(1)一定. (2)①若A=0,则y=- ,表示与y轴垂直的一条直线. ②若B=0,则x=- ,表示与x轴垂直的一条直线. ③若C=0,则Ax+By=0,表示过原点的一条直线. 𝑪 𝑨 𝑪 𝑩

导航 课堂·重难突破 直线的一般式方程与其他形式的转化 典例剖析 1()下列直线中,斜率为专,且不经过第一象限的是( A.3x+4y+7=0 B.4x+3y+7=0 C.4x+3y-42=0 D.3x+4y-42=0 (2)直线V3x-5y+9=0在x轴上的截距等于( A.V3 B.-5 c唱 D.-3V3
导航 课堂·重难突破 一 直线的一般式方程与其他形式的转化 典例剖析 1.(1)下列直线中,斜率为- ,且不经过第一象限的是( ) A.3x+4y+7=0 B.4x+3y+7=0 C.4x+3y-42=0 D.3x+4y-42=0 𝟒 𝟑 (2)直线 𝟑x-5y+9=0 在 x 轴上的截距等于( ) A. 𝟑 B.-5 C. 𝟗 𝟓 D.-3 𝟑

导航 答案:(1)B(2)D 解析:()将一鞭式化为斜截式,斜率为-专的有B,C两项 又(0,14)满足选项C中的方程,即直线经过第一象限,不满足要 求,故选B. (2)令y=0,解得x=3V3.故选D
导航 答案:(1)B (2)D 解析:(1)将一般式化为斜截式,斜率为- 的有B,C两项. 又(0,14)满足选项C中的方程,即直线经过第一象限,不满足要 求,故选B. (2)令y=0,解得x=-3 .故选D. 𝟒 𝟑 𝟑

导 规律总结求直线的一般式方程的策略: )当40时,方程可化为x+只0,只需确定号的值;诺B0 则方程化为会+0,只需确定会合的值因此,只要给出两个 条件,就可以求出直线方程 (2)在求直线方程时,设一般式方程有时并不简单,通常先根据 给定条件选用四种特殊形式之一求方程,再转化为一般式
导航 规律总结 求直线的一般式方程的策略: (1)当 A≠0时,方程可化为 x+𝑩 𝑨 y+𝑪 𝑨 =0,只需确定𝑩 𝑨 , 𝑪 𝑨 的值;若 B≠0, 则方程化为𝑨 𝑩 x+y+𝑪 𝑩 =0,只需确定𝑨 𝑩 , 𝑪 𝑩 的值.因此,只要给出两个 条件,就可以求出直线方程. (2)在求直线方程时,设一般式方程有时并不简单,通常先根据 给定条件选用四种特殊形式之一求方程,再转化为一般式