
全程设计 第2课时】 用空间向量研究直线、平面 的垂直关系
第2课时 用空间向量研究直线、平面 的垂直关系
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练

导航 素养·目标定位 目标素养 知识概览 1.能用向量语言表述直 线与直线、直线与平面、 平面与平面的垂直关系. 用空间向量证明线线垂直 2.会用直线的方向向量 用空间向量研 究直线、平面 用空间向量证明线面垂直 及平面的法向量证明直 的垂直关系 用空间向量证明面面垂直 线与直线、直线与平面 及平面与平面的垂直问 题
导航 素养·目标定位 目 标 素 养 知 识 概 览 1.能用向量语言表述直 线与直线、直线与平面、 平面与平面的垂直关系. 2.会用直线的方向向量 及平面的法向量证明直 线与直线、直线与平面 及平面与平面的垂直问 题
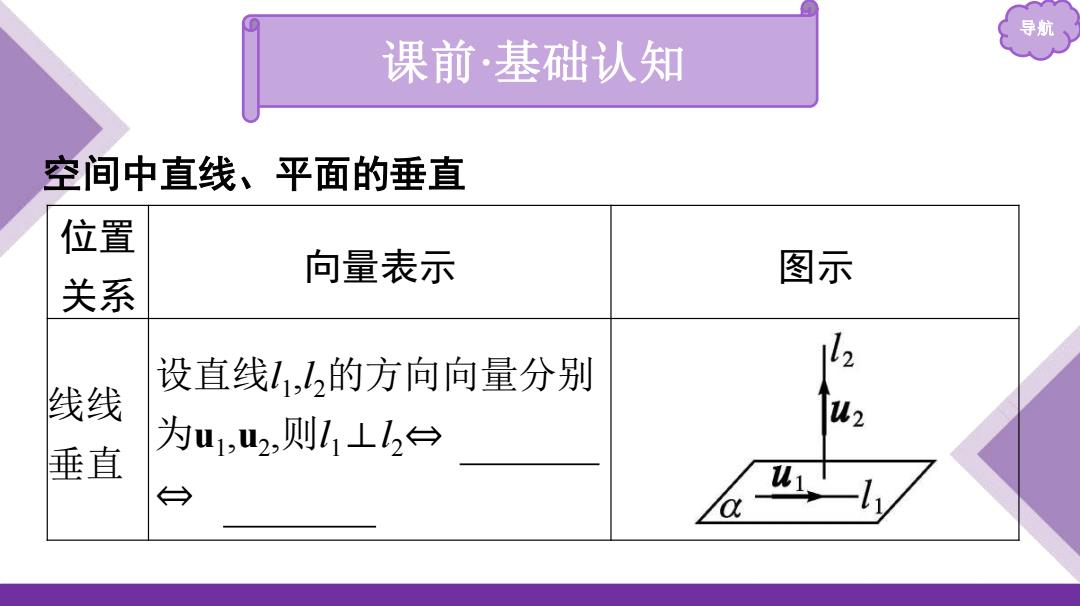
导航 课前·基础认知 空间中直线、平面的垂直 位置 向量表示 图示 关系 设直线1,1,的方向向量分别 12 线线 为u1,2,则l1⊥12→ u2 垂直 台
导航 课前·基础认知 空间中直线、平面的垂直 位置 关系 向量表示 图示 线线 垂直 设直线l1 ,l2的方向向量分别 为u1 ,u2 ,则l1⊥l2⇔ u1⊥u2 ⇔ u1·u2 =0
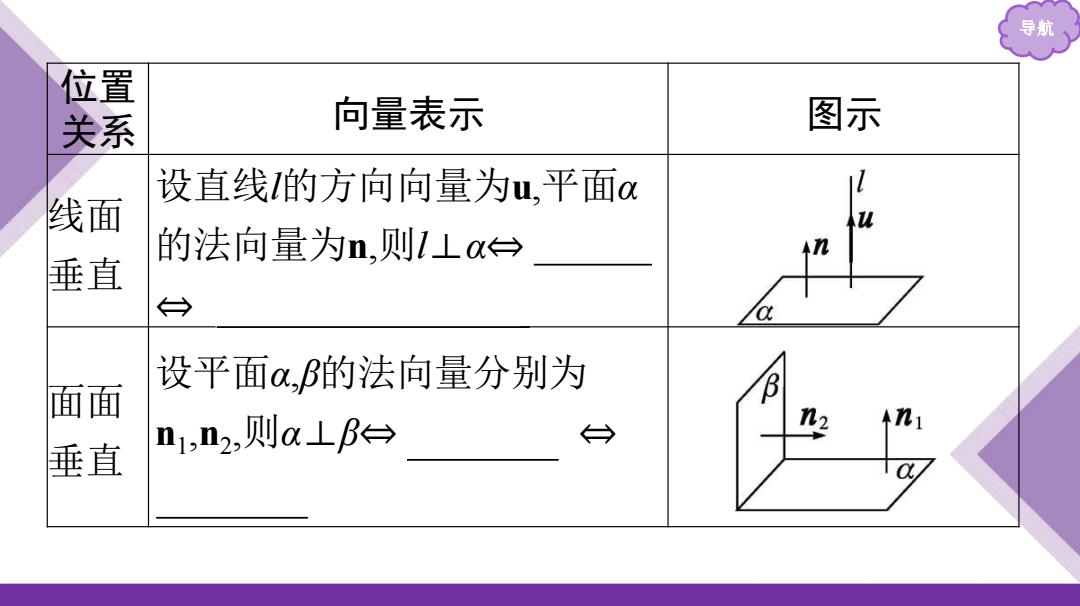
导航 位置 关系 向量表示 图示 设直线的方向向量为u,平面 线面 的法向量为n,则1La台 垂直 → 设平面α,B的法向量分别为 面面 B n1,n2,则a⊥B台 ←→ 2 垂直
导航 位置 关系 向量表示 图示 线面 垂直 设直线 l的方向向量为 u ,平面 α 的法向量为 n , 则 l ⊥ α ⇔ u ∥ n ⇔ ∃ λ ∈ R ,使得 u = λ n 面面 垂直 设平面 α ,β的法向量分别为 n 1 , n 2 , 则 α ⊥ β ⇔ n 1 ⊥ n 2 ⇔ n 1 · n 2 = 0

微训练若平面a1平面A平面a的个法向量为m-((21,2)则 平面的法向量m可以为(C) A(1,2) B.(2,-1,0) C.(1,2,0) D(61,2) 解析:.平面aL平面B,∴n=0. 将选项代入验证,可知C满足.故选C
导航 微训练若平面α⊥平面β,平面α的一个法向量为n= ,则 平面β的法向量m可以为( ) -2,1, 1 2 A. -1, 1 2 , 1 4 B.(2,-1,0) C.(1,2,0) D. 1 2 ,1,2 C 解析:∵平面α⊥平面β,∴n·m=0. 将选项代入验证,可知C满足.故选C
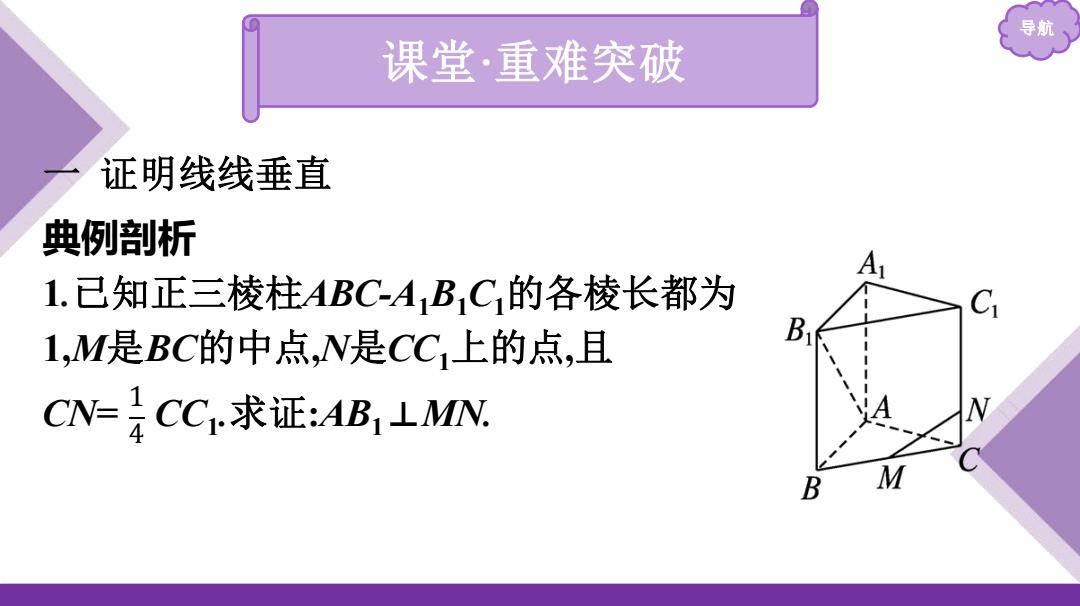
导航 课堂·重难突破 证明线线垂直 典例剖析 A 1.已知正三棱柱ABC-A B C,的各棱长都为 C 1,M是BC的中点,N是CC上的点,且 B CN=CC1,求证:AB1⊥MN
导航 课堂·重难突破 一 证明线线垂直 典例剖析 1.已知正三棱柱ABC-A1B1C1的各棱长都为 1,M是BC的中点,N是CC1上的点,且 CN= CC1 .求证:AB1⊥MN. 1 4

导航 证明:如图,以AB的中点O为原点,建立空间直角坐标系. 由已知得1(20,0),M(0),N(0,),B1(20,1, 所以MN-(是),AB-(1,01, B 所以MN.AB1-+0+}0. 所以MN⊥AB,所以AB1⊥MN
导航 证明:如图,以AB的中点O为原点,建立空间直角坐标系. 由已知得,A - 𝟏 𝟐 ,0,0 ,M 𝟏 𝟒 , 𝟑 𝟒 ,0 ,N 0, 𝟑 𝟐 , 𝟏 𝟒 ,B1 𝟏 𝟐 ,0,1 , 所以𝑴 𝑵 = - 𝟏 𝟒 , 𝟑 𝟒 , 𝟏 𝟒 ,𝑨𝑩𝟏 =(1,0,1), 所以𝑴 𝑵 ·𝑨𝑩𝟏 =- 𝟏 𝟒 +0+ 𝟏 𝟒 =0. 所以𝑴 𝑵 ⊥ 𝑨𝑩𝟏 ,所以 AB1⊥MN

规律总结利用空间向量证明两条直线垂直的常用方法及步 骤: ()基向量法 ①选取三个不共面的已知向量(通常是它们的模及其两两夹 角为已知)为空间的一个基底; ②把两条直线的方向向量用基底表示; ③利用向量的数量积运算,计算出两条直线的方向向量的数 量积为0,得到方向向量垂直; ④由方向向量垂直得到两条直线垂直
导航 规律总结 利用空间向量证明两条直线垂直的常用方法及步 骤: (1)基向量法 ①选取三个不共面的已知向量(通常是它们的模及其两两夹 角为已知)为空间的一个基底; ②把两条直线的方向向量用基底表示; ③利用向量的数量积运算,计算出两条直线的方向向量的数 量积为0,得到方向向量垂直; ④由方向向量垂直得到两条直线垂直

导期 2)坐标法 ①根据已知条件和图形特征,建立适当的空间直角坐标系,正 确地写出各点的坐标; ②根据所求出的点的坐标求出两条直线的方向向量的坐标; ③计算出两条直线的方向向量的数量积为0,得到方向向量垂 直; ④由方向向量垂直得到两条直线垂直
导航 (2)坐标法 ①根据已知条件和图形特征,建立适当的空间直角坐标系,正 确地写出各点的坐标; ②根据所求出的点的坐标求出两条直线的方向向量的坐标; ③计算出两条直线的方向向量的数量积为0,得到方向向量垂 直; ④由方向向量垂直得到两条直线垂直