
全程设计 章末核心素养整合
章末核心素养整合

知识体系构建 专题归纳突破
知识体系构建 专题归纳突破
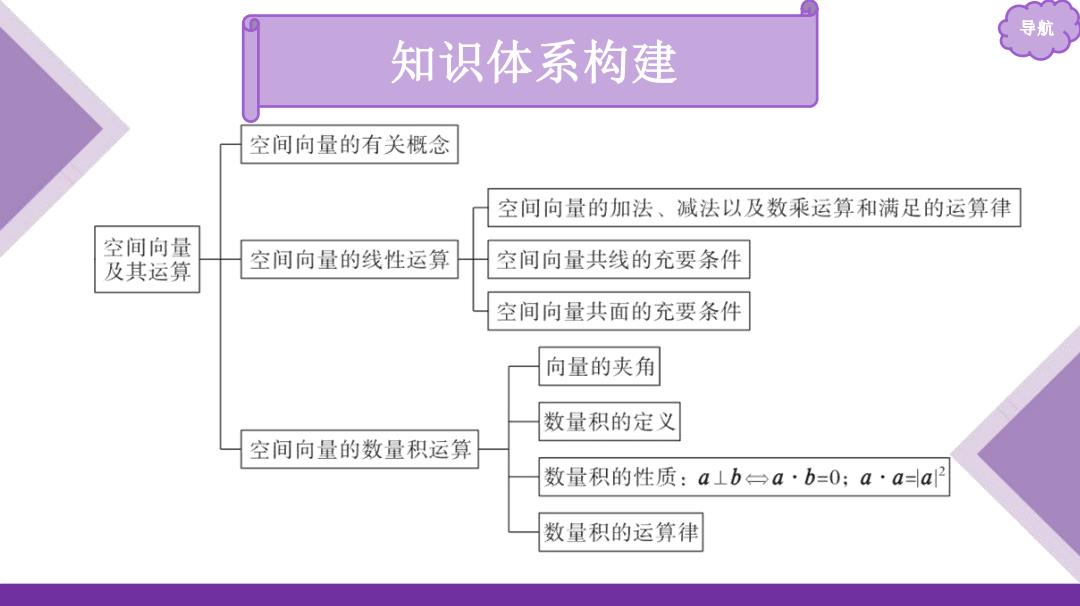
导航 知识体系构建 空间向量的有关概念 空间向量的加法、减法以及数乘运算和满足的运算律 空间向量 及其运算 空间向量的线性运算 空间向量共线的充要条件 空间向量共面的充要条件 向量的夹角 数量积的定义 空间向量的数量积运算 数量积的性质:a⊥b台a·b=0:a·a=a2 数量积的运算律
导航 知识体系构建
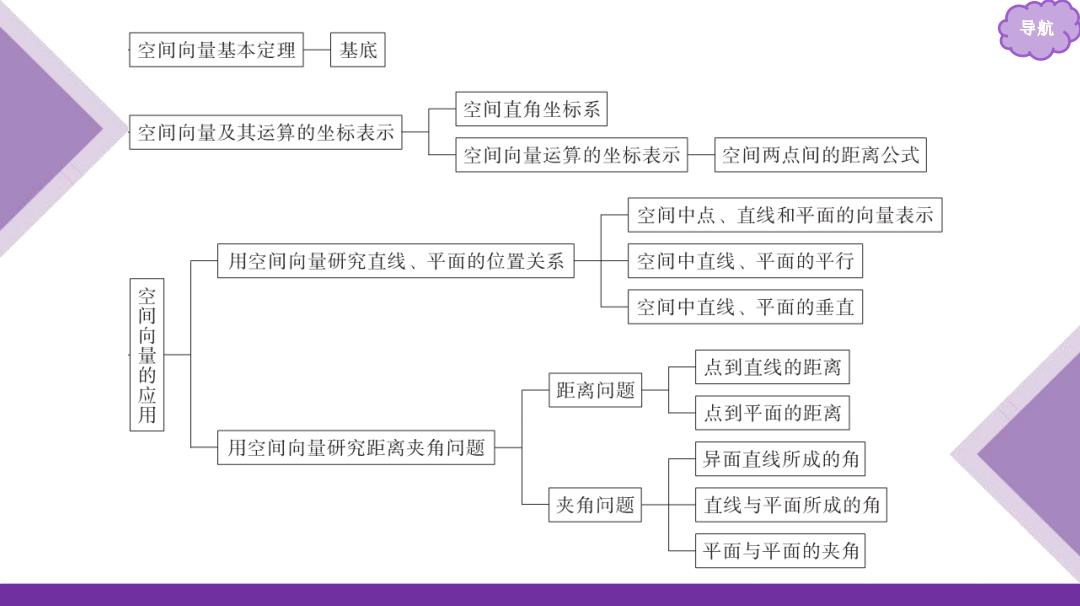
导航 空间向量基本定理 基底 空间直角坐标系 空间向量及其运算的坐标表示 空间向量运算的坐标表示 空间两点间的距离公式 空间中点、直线和平面的向量表示 用空间向量研究直线、平面的位置关系 空间中直线、平面的平行 空间中直线、平面的垂直 空间向量的应用 点到直线的距离 距离问题 点到平面的距离 用空间向量研究距离夹角问题 异面直线所成的角 夹角问题 直线与平面所成的角 平面与平面的夹角
导航

专题归纳突破 专题一空间向量的运算 空间向量的运算主要包括空间向量的线性运算、数量积运算 以及空间向量运算的坐标表示空间向量的运算法则、运算 律与平面向量基本一致 空间向量的运算是利用空间向量解题的前提和基础,其中空 间向量运算的坐标表示是将立体几何中的证明、计算问题转 化成代数问题的重要途径
导航 专题归纳突破 专题一空间向量的运算 空间向量的运算主要包括空间向量的线性运算、数量积运算 以及空间向量运算的坐标表示.空间向量的运算法则、运算 律与平面向量基本一致. 空间向量的运算是利用空间向量解题的前提和基础,其中空 间向量运算的坐标表示是将立体几何中的证明、计算问题转 化成代数问题的重要途径

导航 典型例题1】已知a=(2,-3,5),b=(-3,1,-4) (1)若c=(m,2,m),且ac,求c; (2)若p=(1x,y),且a⊥p,b⊥P,求p 解:(1).allc,∴.c=a, 即(m,2,n)=(2,-3,5), 2 m=2λ, =- ∴.2=-31,解得 m 3 -(2,9) n=51, m 三 3
导航 【典型例题1】已知a=(2,-3,5),b=(-3,1,-4). (1)若c=(m,2,n),且a∥c,求c; (2)若p=(1,x,y),且a⊥p,b⊥p,求p. 解:(1)∵a∥c,∴c=λa, 即(m,2,n)=λ(2,-3,5), ∴ 𝑚 = 2𝜆, 2 = -3𝜆, 𝑛 = 5𝜆, 解得 𝜆 = - 2 3 , 𝑚 = - 4 3 , 𝑛 = - 10 3 . ∴c= - 4 3 ,2,- 10 3

导航、 (2).'aLp,b⊥p, .ap=0,bp=0, 0 x=1, y=-1. ∴.p=(1,-1,-1)
导航 (2)∵a⊥p,b⊥p, ∴a·p=0,b·p=0, ∴ 2-3𝑥 + 5𝑦 = 0, -3 + 𝑥-4𝑦 = 0, 解得 𝑥 = -1, 𝑦 = -1. ∴p=(1,-1,-1)

导 专题二空间向量与空间中线、面的位置关系 设两条不同的直线l,m的方向向量分别为a,b,两个不同的平面 a,B的法向量分别为u,y,直线l¢平面α,则 (1)线线平行:lIlm台→aIlb台a=kb,k∈R; (2)线面平行:lIlo台a⊥u台au=0; (3)面面平行:aIB←台→uIv台u=kw,k∈R, (4)线线垂直:lLm→a⊥b台ab=0; (5)线面垂直:l⊥a台alu台a=ku,k∈R; (6)面面垂直:0⊥台u⊥v台→uv=0
导航 专题二空间向量与空间中线、面的位置关系 设两条不同的直线l,m的方向向量分别为a,b,两个不同的平面 α,β的法向量分别为u,v,直线l⊄平面α,则 (1)线线平行:l∥m⇔a∥b⇔a=kb,k∈R; (2)线面平行:l∥α⇔a⊥u⇔a·u=0; (3)面面平行:α∥β⇔u∥v⇔u=kv,k∈R; (4)线线垂直:l⊥m⇔a⊥b⇔a·b=0; (5)线面垂直:l⊥α⇔a∥u⇔a=ku,k∈R; (6)面面垂直:α⊥β⇔u⊥v⇔u·v=0
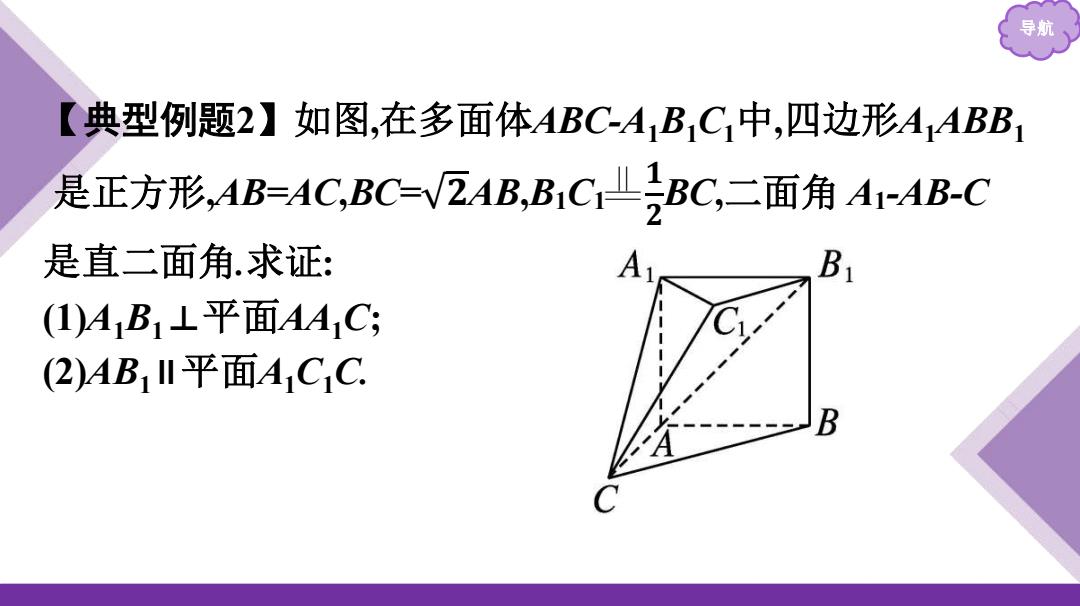
导 【典型例题2】如图,在多面体ABCA1B1C1中,四边形AABB1 是正方形,AB=AC,BC=V2AB,B1C1LBC,二面角AI-AB-C 是直二面角.求证: B (1)AB1⊥平面AAC; (2)AB1II平面AC1C
导航 【典型例题2】如图,在多面体ABC-A1B1C1中,四边形A1ABB1 是正方形,AB=AC,BC= 𝟐AB,B1C1 𝟏 𝟐 BC,二面角 A1-AB-C 是直二面角.求证: (1)A1B1⊥平面AA1C; (2)AB1∥平面A1C1C

导航 证明:.二面角A1AB-C是直二面角, .∴,平面AABB1⊥平面ABC 又四边形A1ABB1是正方形,'AA1LAB .∴AA1⊥平面ABC ∴AA1⊥AC 又AB=AC,BC=V2AB, ∴.∠CAB=90°,即AC⊥AB. .∴AB,AC,AA1两两互相垂直
导航 证明:∵二面角A1 -AB-C是直二面角, ∴平面A1ABB1⊥平面ABC. 又四边形A1ABB1是正方形,∴AA1⊥AB. ∴AA1⊥平面ABC. ∴AA1⊥AC. 又 AB=AC,BC= 𝟐AB, ∴∠CAB=90° ,即AC⊥AB. ∴AB,AC,AA1两两互相垂直