
全程设计 8.6.1 直线与直线垂直
8.6.1 直线与直线垂直

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 异面直线所成的角 (1)定义:已知两条异面直线,b,经过空间任一点0分别作直 线a'∥a,b'∥b,我们把直线a'与b所成的角叫做异面直线a与b 所成的角(或夹角) (2)异面直线所成的角0 的取值范围:0°<90°·
导航 课前·基础认知 异面直线所成的角 (1)定义:已知两条异面直线a,b,经过空间任一点O分别作直 线a'∥a,b'∥b,我们把直线a'与b'所成的角叫做异面直线a与b 所成的角(或夹角). (2)异面直线所成的角θ 的取值范围:0°<θ≤90°
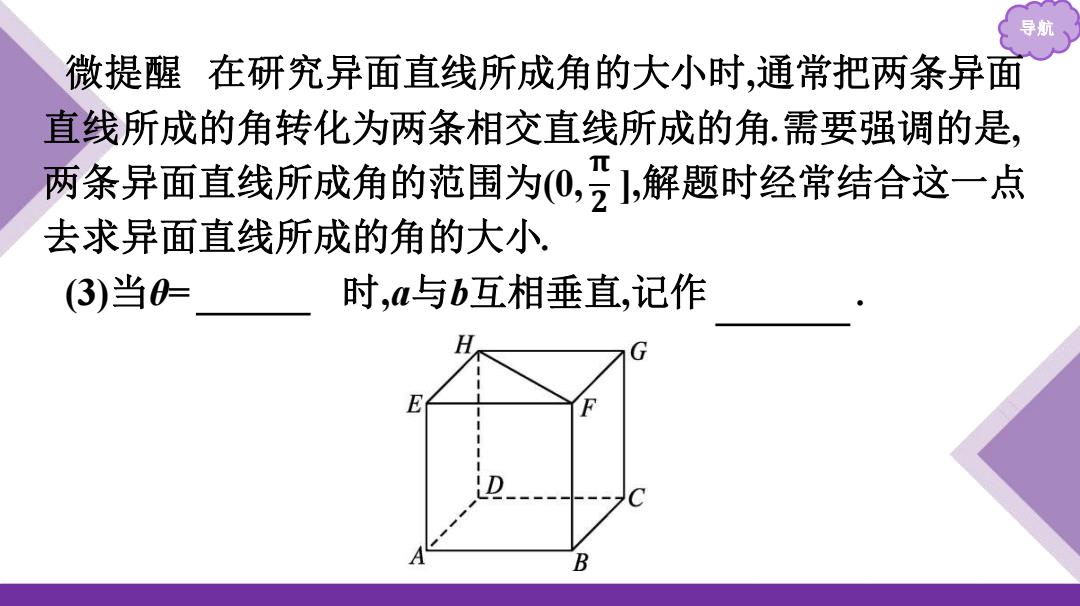
导航 微提醒在研究异面直线所成角的大小时,通常把两条异面 直线所成的角转化为两条相交直线所成的角.需要强调的是, 两条异面直线所成角的范围为0,],解题时经常结合这一点 去求异面直线所成的角的大小 (3)当0= 时,a与b互相垂直,记作 B
导航 微提醒 在研究异面直线所成角的大小时,通常把两条异面 直线所成的角转化为两条相交直线所成的角.需要强调的是, 两条异面直线所成角的范围为(0, ],解题时经常结合这一点 去求异面直线所成的角的大小. (3)当θ= 90° 时,a与b互相垂直,记作 a⊥b . 𝛑 𝟐

微探究1(1)在平面内,两条直线相交成四个角,其中不大于 90°的角称为它们的夹角,用以刻画两直线的错开程度.如图,在 正方体ABCD-EFGH中,如何刻画异面直线AB与HF的错开程度? 应用了什么数学思想? 提示:平移转化成相交直线所成的角,由于AB∥EF,可用EF 与HF的夹角来刻画.应用的是转换思想,即化空间图形问题为 平面图形问题. (2)异面直线所成的角的范围如何?什么是异面直线垂直? 提示:异面直线所成角的范围为(0°,90°],如果两条异面直 线a,b所成的角为直角,我们就称这两条直线互相垂直,记为⊥b
导航 微探究1 (1)在平面内,两条直线相交成四个角,其中不大于 90°的角称为它们的夹角,用以刻画两直线的错开程度.如图,在 正方体ABCD-EFGH中,如何刻画异面直线AB与HF的错开程度? 应用了什么数学思想? 提示:平移转化成相交直线所成的角,由于AB∥EF,可用EF 与HF的夹角来刻画.应用的是转换思想,即化空间图形问题为 平面图形问题. (2)异面直线所成的角的范围如何?什么是异面直线垂直? 提示:异面直线所成角的范围为(0°,90°],如果两条异面直 线a,b所成的角为直角,我们就称这两条直线互相垂直,记为a⊥b

导航 微探究2作异面直线所成的角,有哪些方法? 提示:主要有三种方法: ①直接平移法(可利用图中已有的平行线); ②中位线平移法; ③补形平移法(在已知图形中,补作一个相同的几何体,以便 找到平行线)
导航 微探究2 作异面直线所成的角,有哪些方法? 提示:主要有三种方法: ①直接平移法(可利用图中已有的平行线); ②中位线平移法; ③补形平移法(在已知图形中,补作一个相同的几何体,以便 找到平行线)
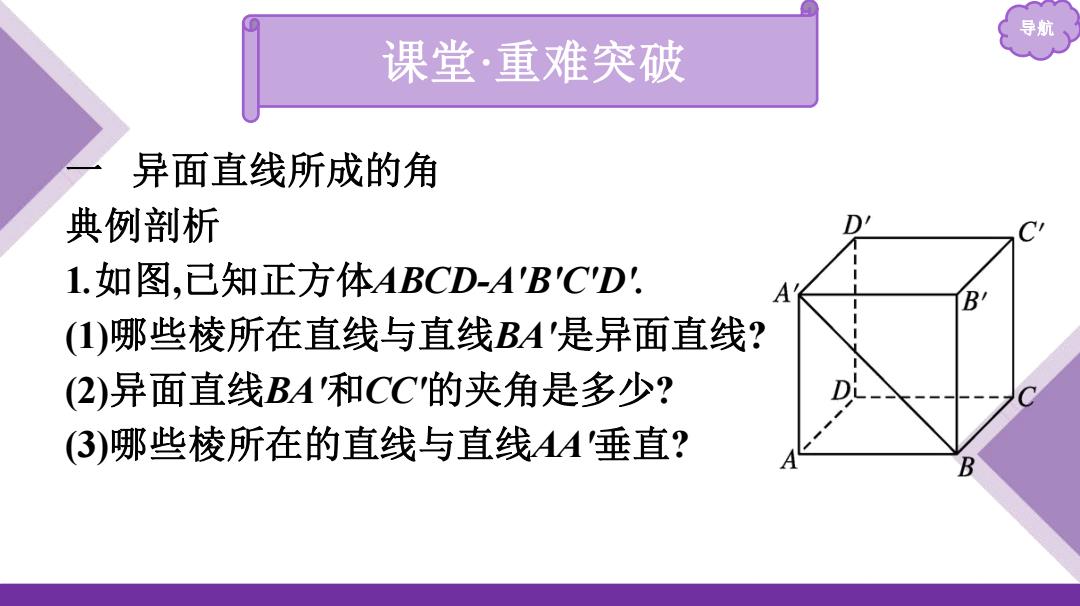
导航 课堂·重难突破 异面直线所成的角 典例剖析 D' 1.如图,己知正方体ABCD-A'B'CD! A (1)哪些棱所在直线与直线BA'是异面直线? (2)异面直线BA'和CC的夹角是多少? 3)哪些棱所在的直线与直线AA垂直? B
导航 课堂·重难突破 一 异面直线所成的角 典例剖析 1.如图,已知正方体ABCD-A'B'C'D'. (1)哪些棱所在直线与直线BA'是异面直线? (2)异面直线BA'和CC'的夹角是多少? (3)哪些棱所在的直线与直线AA'垂直?

导 解:(1)由异面直线的定义可知,棱 AD,DC,CC,DD',D'C',B'C所在直线分别与直线BA'是异面直 线 (2)由BB'∥CC可知,∠BBA'为异面直线BA'和CC的夹 角,∠B'BA=45°,所以异面直线BA'和CC的夹角为45° (3)直线AB,BC,CD,DA,A'B',B'C',CD',D'A'分别与直线AA' 垂直
导航 解:(1)由异面直线的定义可知,棱 AD,DC,CC',DD',D'C',B'C'所在直线分别与直线BA'是异面直 线. (2)由BB'∥CC'可知,∠B'BA'为异面直线BA'和CC'的夹 角,∠B'BA'=45° ,所以异面直线BA'和CC'的夹角为45° . (3)直线AB,BC,CD,DA,A'B',B'C',C'D',D'A'分别与直线AA' 垂直

导期 规律总结求两条异面直线所成的角的步骤 ()用平移法,将两条异面直线平移,使平移后的两条直线相 交于一点 (2)找出两条直线所成的角,即为两条异面直线所成的角 3)求出角的值,常利用解三角形得出. 提醒:异面直线所成角的范围是(0,2]·
导航 规律总结 求两条异面直线所成的角的步骤 (1)用平移法,将两条异面直线平移,使平移后的两条直线相 交于一点. (2)找出两条直线所成的角,即为两条异面直线所成的角. (3)求出角的值,常利用解三角形得出. 提醒:异面直线所成角的范围是(0, ]. 𝛑 𝟐
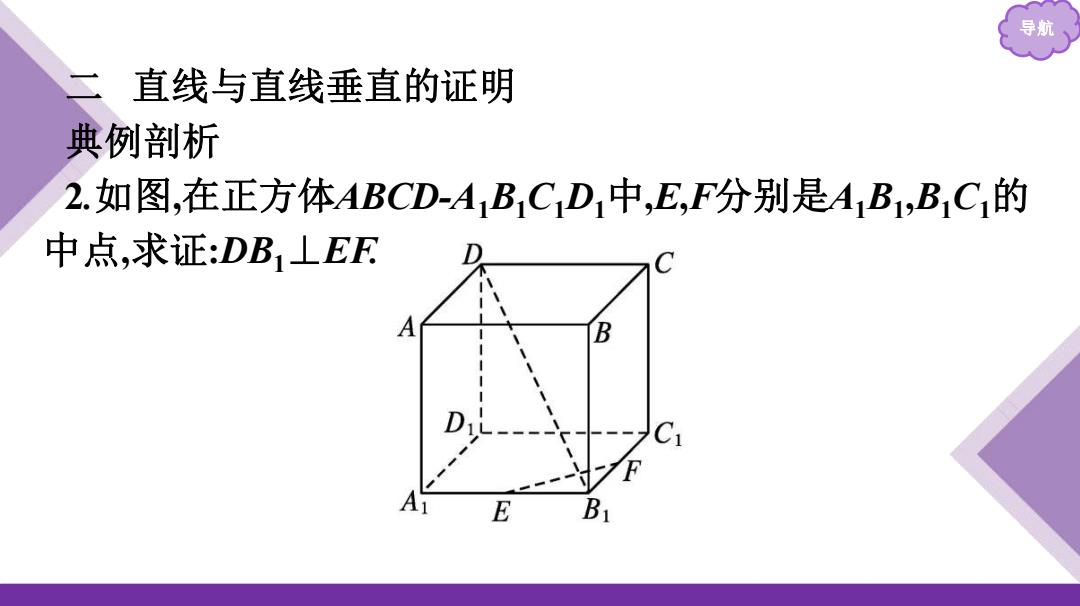
导航 二直线与直线垂直的证明 典例剖析 2如图,在正方体ABCD-A1B1C1D1中,E,F分别是A1B1,BC1的 中点,求证:DB1⊥EF
导航 二 直线与直线垂直的证明 典例剖析 2.如图,在正方体ABCD-A1B1C1D1中,E,F分别是A1B1 ,B1C1的 中点,求证:DB1⊥EF