
全程设计 1.1.2 空间向量的数量积运算
1.1.2 空间向量的数量积运算
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练

导航 素养·目标定位 目标素养 知识概览 1.了解空间向量的夹角的 概念及表示方法 空间向量的夹角 2.掌握两个向量的数量积 空间向量的 的概念、性质、计算与运 数量积运算 空间向量的数量积及其性质 算律. 数量积的应用 3.能用向量的数量积解决 立体几何中的垂直、夹角 长度等问题
导航 素养·目标定位 目 标 素 养 知 识 概 览 1.了解空间向量的夹角的 概念及表示方法. 2.掌握两个向量的数量积 的概念、性质、计算与运 算律. 3.能用向量的数量积解决 立体几何中的垂直、夹角、 长度等问题
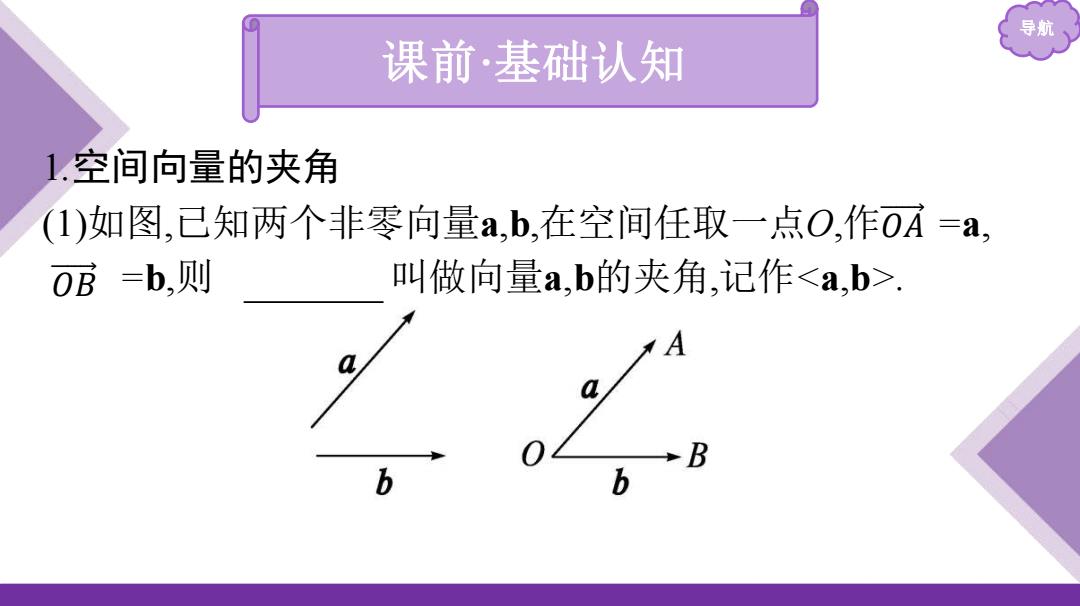
导航 课前·基础认知 1.空间向量的夹角 (1)如图,已知两个非零向量a,b,在空间任取一点O,作0A=a, 0B=b,则 叫做向量a,b的夹角,记作. B
导航 课前·基础认知 1.空间向量的夹角 (1)如图,已知两个非零向量a,b,在空间任取一点O,作 =a, =b,则 ∠AOB 叫做向量a,b的夹角,记作. 𝑂 𝐴 𝑂 𝐵

导航 (2)通常规定,0≤≤π.这样,两个向量的夹角是唯一确定 的,且=.如果-无那么向量a,b互相垂直,记 作a⊥b
导航 (2)通常规定,0≤≤π.这样,两个向量的夹角是唯一确定 的,且=.如果= ,那么向量a,b互相垂直,记 作a⊥b. π 2

导航 2.空间向量的数量积 (1)定义:已知两个非零向量a,b,则 叫做a,b 的数量积,记作ab.即ab= 特别地,零向量 与任意向量的数量积为 (2)性质: ①a⊥b台 ②aa=a acos=
导航 2.空间向量的数量积 (1)定义:已知两个非零向量a,b,则 |a||b|cos 叫做a,b 的数量积,记作a·b.即a·b= |a||b|cos .特别地,零向量 与任意向量的数量积为 0 . (2)性质: ①a⊥b⇔ a·b=0 ; ②a·a=|a||a|cos= |a| 2

导航 (3)运算律: ①(2a)b=(ab),λ∈R; ②ab=ba(交换律); ③a(b+c)=ab+ac(分配律). 微思考数量积运算满足结合律吗? 提示:数量积运算不满足结合律 即(ab)c=a(bc)一般不成立
导航 (3)运算律 : ① (λ a)· b = λ ( a · b), λ ∈R; ② a · b = b · a (交换律); ③ a·( b + c)= a · b + a · c (分配律 ). 微思考数量积运算满足结合律吗 ? 提示 :数量积运算不满足结合律 , 即 ( a · b)· c = a·( b · c )一般不成立
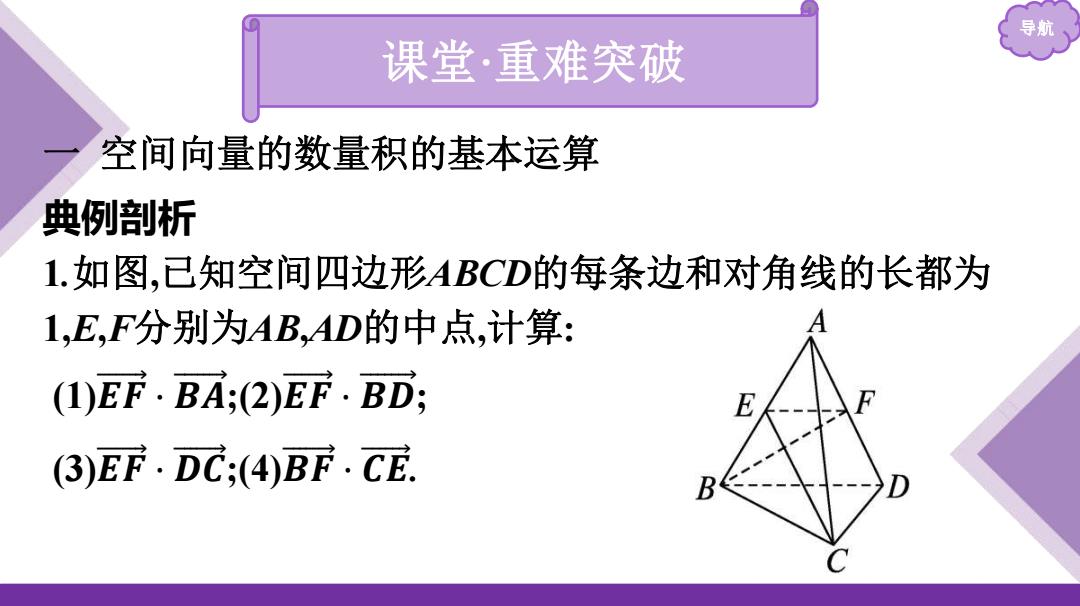
导航 课堂·重难突破 空间向量的数量积的基本运算 典例剖析 1.如图,已知空间四边形ABCD的每条边和对角线的长都为 1,E,F分别为AB,AD的中点,计算: (1)EF.BA;(2)EF.BD; ()EF.DC;(4)BF.CE
导航 课堂·重难突破 一 空间向量的数量积的基本运算 典例剖析 1.如图,已知空间四边形ABCD的每条边和对角线的长都为 1,E,F分别为AB,AD的中点,计算: (1)𝑬 𝑭 ·𝑩 𝑨 ;(2)𝑬 𝑭 ·𝑩 𝑫 ; (3)𝑬 𝑭 ·𝑫 𝑪 ;(4)𝑩 𝑭 ·𝑪 𝑬

导航 解:(EF.BA=2BD.BA BDBAl-cOs x1x1x0s60° 故EF·BA=
导航 解:(1)𝑬 𝑭 ·𝑩 𝑨 = 𝟏 𝟐 𝑩 𝑫 ·𝑩 𝑨 = 𝟏 𝟐 |𝑩 𝑫 |·|𝑩 𝑨 |·cos = 𝟏 𝟐 ×1×1×cos 60°= 𝟏 𝟒 , 故𝑬 𝑭 ·𝑩 𝑨 = 𝟏 𝟒
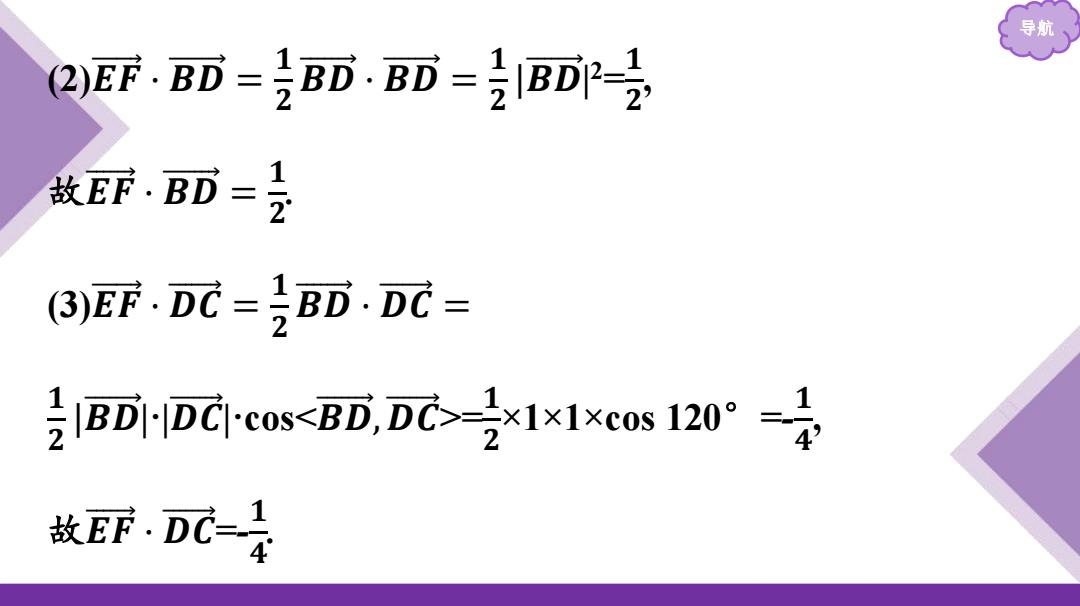
导航 2F.BD=2BD.B而-2BD-2 故EF.BD=2 (3)EF.DC=BD.DC= 2IBD1-DCrc0s<BD,DC1x1×c0s120°=} 故E耶DC-是
导航 (2)𝑬 𝑭 ·𝑩 𝑫 = 𝟏 𝟐 𝑩 𝑫 ·𝑩 𝑫 = 𝟏 𝟐 |𝑩 𝑫 | 2 = 𝟏 𝟐 , 故𝑬 𝑭 ·𝑩 𝑫 = 𝟏 𝟐 . (3)𝑬 𝑭 ·𝑫 𝑪 = 𝟏 𝟐 𝑩 𝑫 ·𝑫 𝑪 = 𝟏 𝟐 |𝑩 𝑫 |·|𝑫 𝑪 |·cos= 𝟏 𝟐 ×1×1×cos 120°=- 𝟏 𝟒 , 故𝑬 𝑭 ·𝑫 𝑪 =- 𝟏 𝟒