
全程设计 章末核心素养整合
章末核心素养整合

知识体系构建 专题归纳突破
知识体系构建 专题归纳突破

导航 知识体系构建 定义:平面内与两个定点F,F,的距离的和等于常数大于FF,)的点的轨迹 =1(a>b>0) 标准方程 椭圆及其方程 焦点在轴上:二+号 +方=1a>b>0 顶点:(±a,0),(0,±b)或(0,±a),(±b,0) 对称轴:x轴、轴 对称中心:原点 几何性质 长轴长2a,短轴长2b,焦距2c 参数a,b,c的关系:a2-b2+c2 离心率e=0<e<l)
导航 知识体系构建
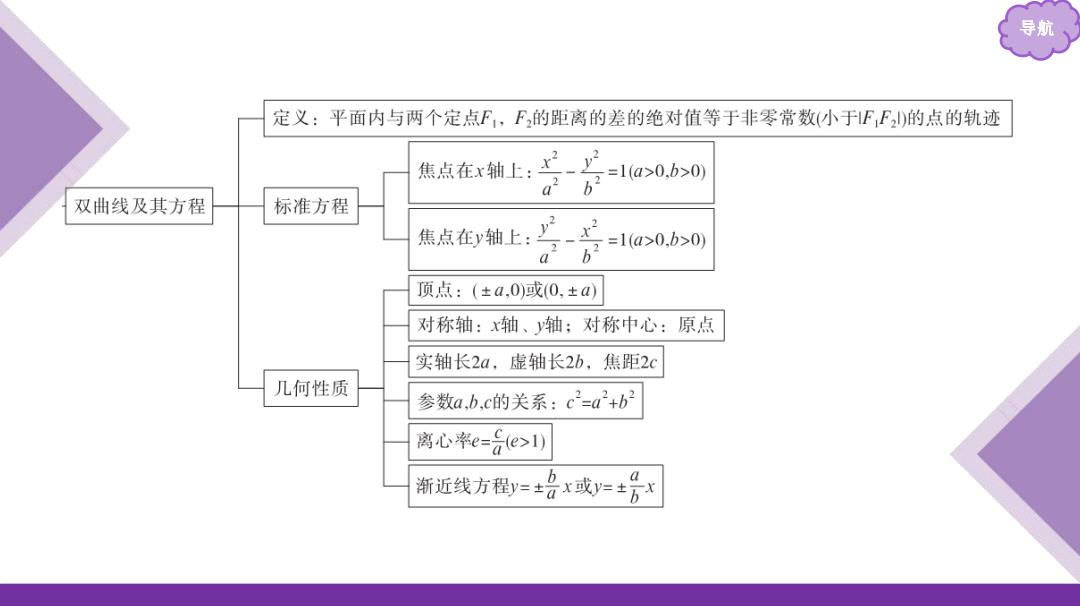
导航 定义:平面内与两个定点F,F,的距离的差的绝对值等于非零常数(小于F,F,)的点的轨迹 焦点在x轴上:女y =1(a>0,b>0) a2 b2 双曲线及其方程 标准方程 焦点在y轴上:二-号=1a>0.b>0 0 b 顶点:(±a.0)或(0,±a) 对称轴:x轴、轴:对称中心:原点 实轴长2a,虚轴长2b,焦距2c 几何性质 参数a,b,c的关系:c2=a2+b2 离心率e=e>l) 渐近线方程=±名x或=±号x
导航
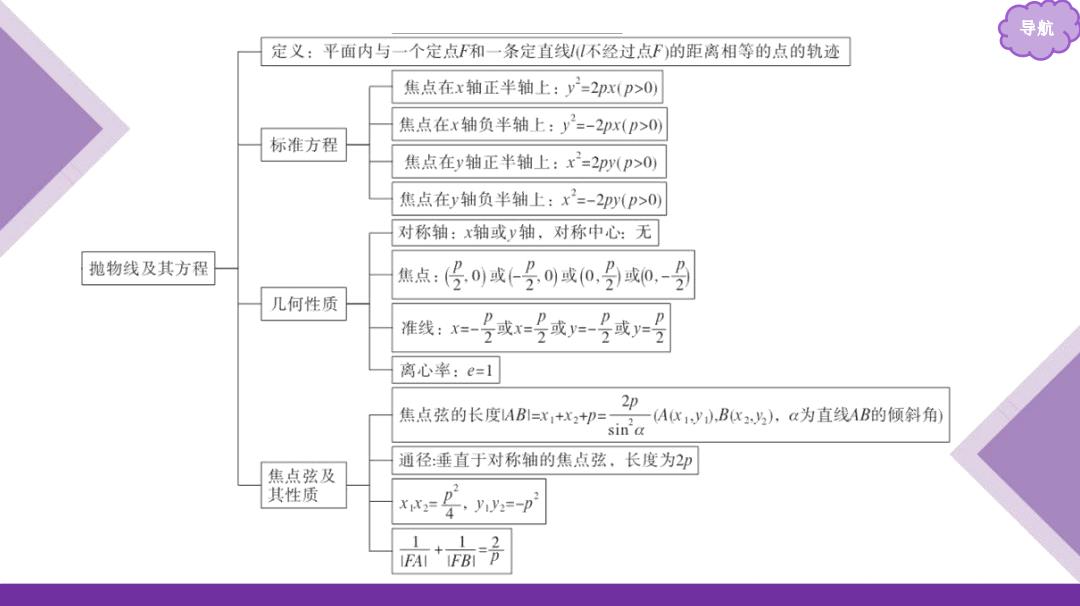
导航 定义:平面内与一个定点F和一条定直线不经过点F)的距离相等的点的轨迹 焦点在x轴正半轴上:y=2px(p>0) 焦点在x轴负半轴上:y2=-2px(p>0) 标准方程 焦点在y轴正半轴上:x=2py(p>0) 焦点在y轴负半轴上:x2=-2y(p>0) 对称轴:x轴或y轴,对称中心:无 抛物线及其方程 焦点:兮0)或←号0或0,号或0-号 几何性质 准线:X=-号或x=号或归-号或)=号 离心率:e=1 2p 焦点弦的长度AB=x,+x2+p= (A代1y,B代),a为直线AB的倾斜角) sin'a 通径:垂直于对称轴的焦点弦,长度为2印 焦点弦及 其性质 D xx=号,=-p 1 IFAI IFBI P
导航
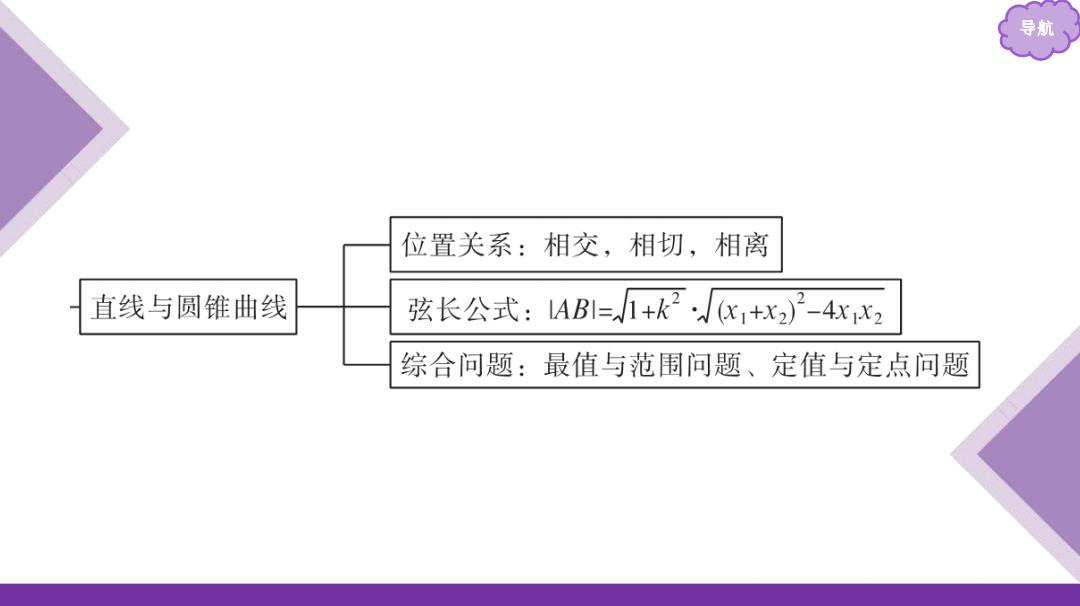
导航、 位置关系:相交,相切,相离 直线与圆锥曲线 弦长公式:AB1=+k2K1+x2)-4xx2 综合问题:最值与范围问题、定值与定点问题
导航

导 专题归纳突破 专题一圆推曲线定义的应用 解决圆锥曲线的问题,要有优先运用圆锥曲线定义解题的意 识,“回归定义”“双向应用”是一种重要的解题策略 (1)在求动点的轨迹以及轨迹方程问题中,若所求动点的轨迹 符合某种圆锥曲线的定义,则可直接根据定义求得其轨迹(方 程) (2)涉及椭圆、双曲线的焦点三角形问题时,通常利用定义结 合解三角形的有关知识求解
导航 专题归纳突破 专题一圆锥曲线定义的应用 解决圆锥曲线的问题,要有优先运用圆锥曲线定义解题的意 识,“回归定义”“双向应用”是一种重要的解题策略. (1)在求动点的轨迹以及轨迹方程问题中,若所求动点的轨迹 符合某种圆锥曲线的定义,则可直接根据定义求得其轨迹(方 程). (2)涉及椭圆、双曲线的焦点三角形问题时,通常利用定义结 合解三角形的有关知识求解

导航 3)在解决抛物线的问题时,常利用定义将抛物线上的点到焦 点的距离与点到准线的距离相互转化,从而简化问题的求解 过程
导航 (3)在解决抛物线的问题时,常利用定义将抛物线上的点到焦 点的距离与点到准线的距离相互转化,从而简化问题的求解 过程

导航 【典型例题1】已知圆x+2)2+y2=1的圆心为A,点B(2,0),分别 求出满足下列条件的动点M的轨迹方程. (1)△MAB的周长为10; (2)圆M过点B(2,0)且与圆A外切; 3)圆M与圆A外切且与直线x=1相切
导航 【典型例题1】已知圆(x+2)2+y2=1的圆心为A,点B(2,0),分别 求出满足下列条件的动点M的轨迹方程. (1)△MAB的周长为10; (2)圆M过点B(2,0)且与圆A外切; (3)圆M与圆A外切且与直线x=1相切

导 解:(1)根据题意,知A(-2,0),且MA+MB+AB=10,即 MA+MB1=6>4=AB\, 则点M的轨迹是以A,B为焦点,长轴长等于6的椭圆,于是长 轴长2=6,焦距2c=4,即=3,c=2,所以短半轴长b=5. 因为点M不能与A,B共线,所以y0,故动点M的轨迹方程为 号+告100
导航 解:(1)根据题意,知A(-2,0),且|MA|+|MB|+|AB|=10,即 |MA|+|MB|=6>4=|AB|, 则点M的轨迹是以A,B为焦点,长轴长等于6的椭圆,于是长 轴长 2a=6,焦距 2c=4,即 a=3,c=2,所以短半轴长 b= 𝟓. 因为点 M 不能与 A,B 共线,所以 y≠0,故动点 M 的轨迹方程为 𝒙 𝟐 𝟗 + 𝒚 𝟐 𝟓 =1(y≠0)