
全程设计 2.3.1 两条直线的交点坐标 2.3.2 两点间的距离公式
2.3.1 两条直线的交点坐标 2.3.2 两点间的距离公式

素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
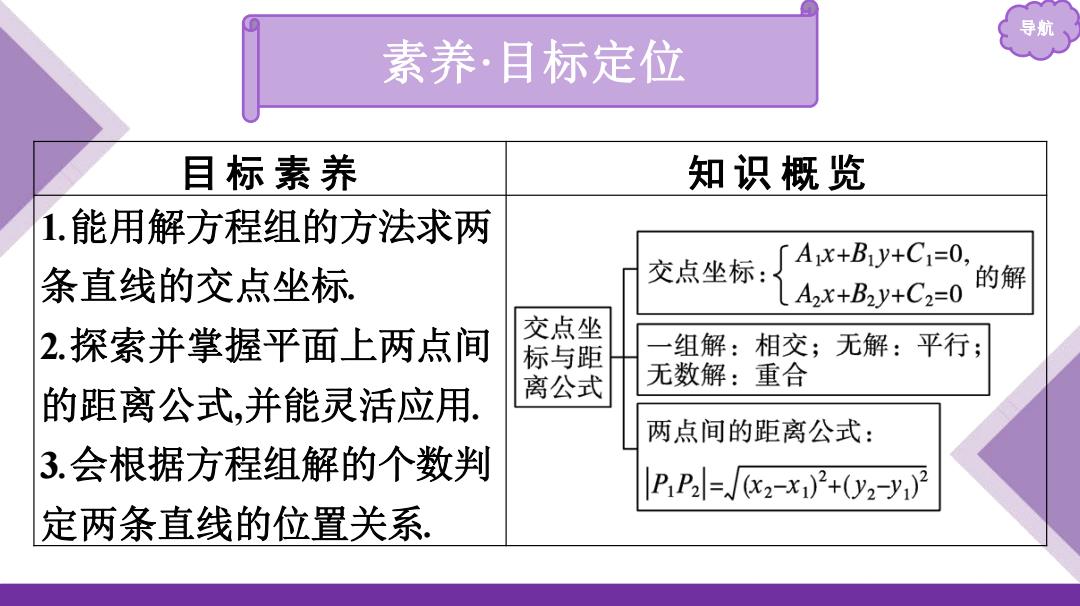
导航 素养·目标定位 目标素养 知识概览 1.能用解方程组的方法求两 条直线的交点坐标 交点坐标:厂Ax+By+C1=0, LA2x+B2y+C2=0 的解 2.探索并掌握平面上两点间 交点坐 标与距 组解:相交;无解:平行; 的距离公式,并能灵活应用. 离公式 无数解:重合 两点间的距离公式: 3.会根据方程组解的个数判 PP2l=02-x)2+(y2-y2 定两条直线的位置关系
导航 素养·目标定位 目 标 素 养 知 识 概 览 1.能用解方程组的方法求两 条直线的交点坐标. 2.探索并掌握平面上两点间 的距离公式,并能灵活应用. 3.会根据方程组解的个数判 定两条直线的位置关系

导航 课前·基础认知 1,两条直线的交点坐标 1)两条直线的交点坐标 几何元素及关系 代数表示 点A A(a,b) 直线 1:Ax+By+C=0 点A在直线L上 直线,与的交点是4方程组+y十8:8的解是
导航 课前·基础认知 1.两条直线的交点坐标 (1)两条直线的交点坐标 几何元素及关系 代数表示 点A A(a,b) 直线l l:Ax+By+C=0 点A在直线l上 Aa+Bb+C=0 直线l1与l2的交点是A 方程组 𝐀𝟏 𝐱 + 𝐁𝟏 𝐲 + 𝐂𝟏 = 𝟎, 𝐀𝟐 𝐱 + 𝐁𝟐 𝐲 + 𝐂𝟐 = 𝟎 的解是 𝐱 = 𝐚, 𝐲 = 𝐛

导 微训练直线x+2y-2=0与直线2x+y-3=0的交点坐标是( A.(4,1) B.(1,4) c(传) D.(G勃 答案:C 解析:解方程组{ x+2y-2=0,得 4 即直线x+2y-2=0与 (2x+y-3=0, y 3, 直线2xt30的交点坐标是(传,)
导航 微训练直线x+2y-2=0与直线2x+y-3=0的交点坐标是( ) A.(4,1) B.(1,4) C. 𝟒 𝟑 , 𝟏 𝟑 D. 𝟏 𝟑 , 𝟒 𝟑 答案:C 解析:解方程组 𝒙 + 𝟐𝒚-𝟐 = 𝟎, 𝟐𝒙 + 𝒚-𝟑 = 𝟎, 得 𝒙 = 𝟒 𝟑 , 𝒚 = 𝟏 𝟑 , 即直线 x+2y-2=0 与 直线 2x+y-3=0 的交点坐标是 𝟒 𝟑 , 𝟏 𝟑
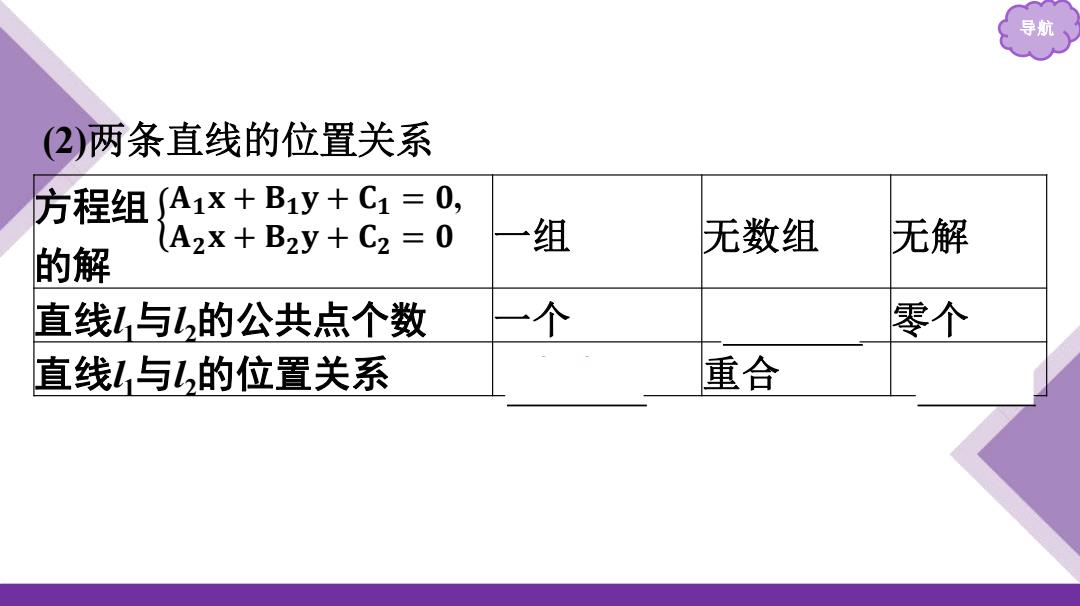
导航 (2)两条直线的位置关系 方程组A1x+B1y+C1=0, (A2X+B2y+C2=0 一组 无数组 无解 的解 直线L,与L,的公共点个数 一个 零个 直线1,与l,的位置关系 重合
导航 (2)两条直线的位置关系 方程组 的解 一组 无数组 无解 直线l1与l2的公共点个数 一个 无数个 零个 直线l1与l2的位置关系 相交 重合 平行 𝐀𝟏 𝐱 + 𝐁𝟏 𝐲 + 𝐂𝟏 = 𝟎, 𝐀𝟐 𝐱 + 𝐁𝟐 𝐲 + 𝐂𝟐 = 𝟎

导航 2.两点间距离公式 平面内两点P(K1y1),P2K2y2)间的距离公式 P1P2= 特别地,原点O0,0)与任一点Px,)间的距离 OPI-
导航 2.两点间距离公式 平面内两点P1 (x1 ,y1 ),P2 (x2 ,y2 )间的距离公式 |P1P2|= (𝒙𝟐-𝒙𝟏) 𝟐 + (𝒚𝟐-𝒚𝟏) 𝟐 . 特别地,原点 O(0,0)与任一点 P(x,y)间的距离 |OP|= 𝒙 𝟐 + 𝒚𝟐

导航 微思考(1)由两条直线方程组成的方程组解的情况与两条直 线的位置关系有何对应关系? (2)两点P1化1y1),P2化2y2)间的距离公式是否可以写成 1PP2斤x1-x2)2+y1-y2)2的形式?
导航 微思考(1)由两条直线方程组成的方程组解的情况与两条直 线的位置关系有何对应关系? (2)两点P1 (x1 ,y1 ),P2 (x2 ,y2 )间的距离公式是否可以写成 |P1P2|= (𝒙𝟏-𝒙𝟐) 𝟐 + (𝒚𝟏-𝒚𝟐) 𝟐 的形式?

导期 提示:(1)①若方程组无解,则11I12;②若方程组有且只有一个 解,则直线11与直线,相交;③若方程组有无数解,则直线11与直 线l2重合. (2)可以,原因是x2-x1)2+y2-y1)2=x1-x2)2+y1-y2)2 也就是说公式中P,P两点的位置没有先后之分
导航 提示:(1)①若方程组无解,则l1∥l2 ;②若方程组有且只有一个 解,则直线l1与直线l2相交;③若方程组有无数解,则直线l1与直 线l2重合. (2)可以,原因是 (𝒙𝟐-𝒙𝟏) 𝟐 + (𝒚𝟐-𝒚𝟏) 𝟐 = (𝒙𝟏-𝒙𝟐) 𝟐 + (𝒚𝟏-𝒚𝟐) 𝟐 , 也就是说公式中 P1,P2两点的位置没有先后之分

导航 微训练已知点A(-2,-1),B(a,3),且AB=5,则的值为( A.1 B.-5 C.1或-5 D.-1或5 答案:C 解析:AB=(a+2)2+(3+1)2=5, ∴.=5或a=1
导航 微训练已知点A(-2,-1),B(a,3),且|AB|=5,则a的值为( ) A.1 B.-5 C.1或-5 D.-1或5 答案:C 解析:∵|AB|= (𝒂 + 𝟐) 𝟐 + (𝟑 + 𝟏) 𝟐 =5, ∴a=-5 或 a=1