
全程设计 微专题一 两个计数原理与排列 组合的应用
微专题一 两个计数原理与排列、 组合的应用

两个计数原理的应用 1分类加法计数原理 任务 完成一件事 有两类不同方案,在第1类方案中有 分类 m种不同的方法,在第2类方案中有n 种不同的方法 计数 完成这件事共有N=m+n种不同的方法
一 两个计数原理的应用 1.分类加法计数原理
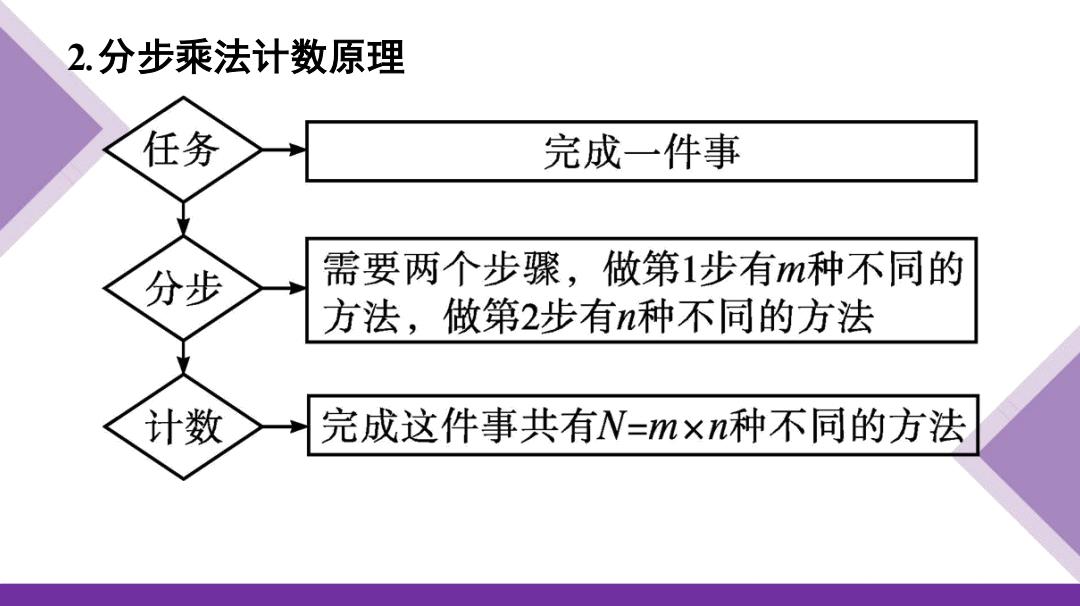
2.分步乘法计数原理 任务 完成一件事 分步 需要两个步骤,做第1步有m种不同的 方法,做第2步有n种不同的方法 计数 完成这件事共有N=m×n种不同的方法
2.分步乘法计数原理

命题角度1:“类中有步”的计数问题 【典型例题1】电视台在某节目中拿出两个信箱,其中存放 着先后两次竞猜中成绩优秀的观众来信,甲信箱中有30封,乙 信箱中有20封,现由主持人抽奖确定幸运观众,若先确定一名 幸运之星,再从两信箱中各确定一名幸运伙伴,则有 种 不同的结果 答案:28800
命题角度1:“类中有步”的计数问题 【典型例题1】电视台在某节目中拿出两个信箱,其中存放 着先后两次竞猜中成绩优秀的观众来信,甲信箱中有30封,乙 信箱中有20封,现由主持人抽奖确定幸运观众,若先确定一名 幸运之星,再从两信箱中各确定一名幸运伙伴,则有 种 不同的结果. 答案:28 800

解析:在甲箱或乙箱中抽取幸运之星,决定了后边选幸运伙 伴是不同的,故要分两类分别计算:第1类,幸运之星在甲箱中 抽,先确定幸运之星,再在两箱中各确定一名幸运伙伴,有 30X29×20=17400种结果;第2类,幸运之星在乙箱中抽,同理 有20×19×30=11400种结果, 因此共有17400+11400=28800种不同的结果
解析:在甲箱或乙箱中抽取幸运之星,决定了后边选幸运伙 伴是不同的,故要分两类分别计算:第1类,幸运之星在甲箱中 抽,先确定幸运之星,再在两箱中各确定一名幸运伙伴,有 30×29×20=17 400种结果;第2类,幸运之星在乙箱中抽,同理 有20×19×30=11 400种结果. 因此共有17 400+11 400=28 800种不同的结果
解题技巧用流程图描述计数问题,类中有步的情形如图所 示 第1类 A m m2 m3 B mi ms 第2类 从A到B算作完成一件事,完成这件事有两类方法,第1类方法 有3步,第2类方法有2步,每步的方法数为m(=1,2,3,4,5), 因此,完成这件事的方法数为(m1m2m3+m4ms) “类”与“步”可进一步地理解为: “类”用“+”号连接,“步”用“义”号连接,“类”独立,“步”连 续,“类”标志一件事的完成,“步”缺一不可
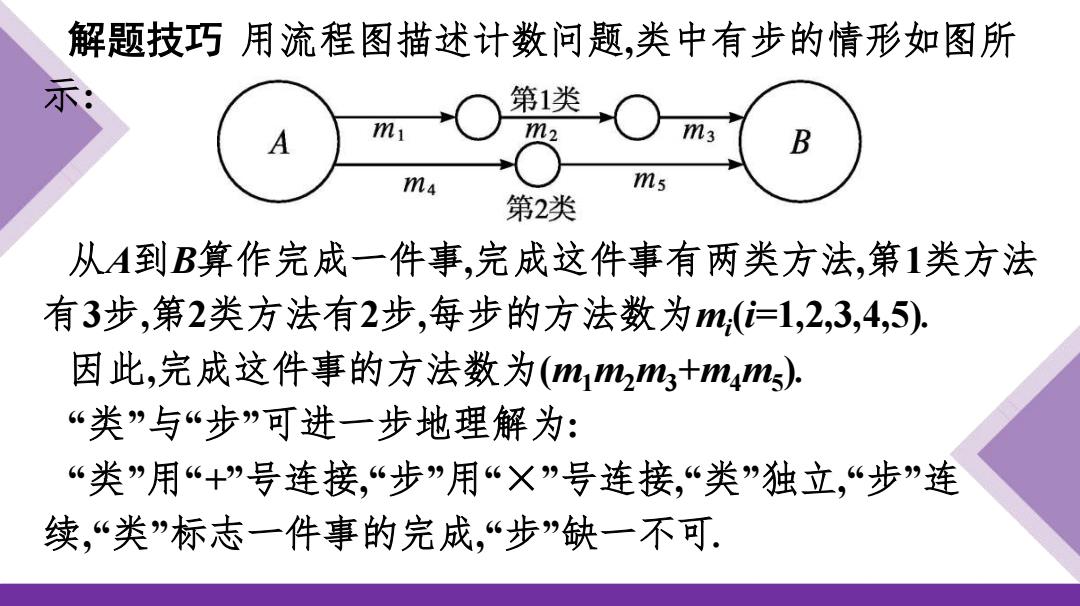
解题技巧 用流程图描述计数问题,类中有步的情形如图所 示: 从A到B算作完成一件事,完成这件事有两类方法,第1类方法 有3步,第2类方法有2步,每步的方法数为mi (i=1,2,3,4,5). 因此,完成这件事的方法数为(m1m2m3+m4m5 ). “类”与“步”可进一步地理解为: “类”用“+”号连接,“步”用“×”号连接,“类”独立,“步”连 续,“类”标志一件事的完成,“步”缺一不可

跟踪训练1现有4种不同颜色,要对四个部 分进行着色,如图所示,要求有公共边界的两 部分不能用同一种颜色,则不同的着色方法 共有() A.24种 B.30种 C.36种 D.48种 答案:D
跟踪训练1现有4种不同颜色,要对四个部 分进行着色,如图所示,要求有公共边界的两 部分不能用同一种颜色,则不同的着色方法 共有( ) A.24种 B.30种 C.36种 D.48种 答案:D
解析:将原图从上而下的4个区域标为1,2,3,4.因为1,2,3之间 不能同色,1与4可以同色,因此,要分类讨论1,4同色与不同色两 种情况.故不同的着色方法种数为4×3×2+4×3×2×1=48. 1 2 3 4 故选D
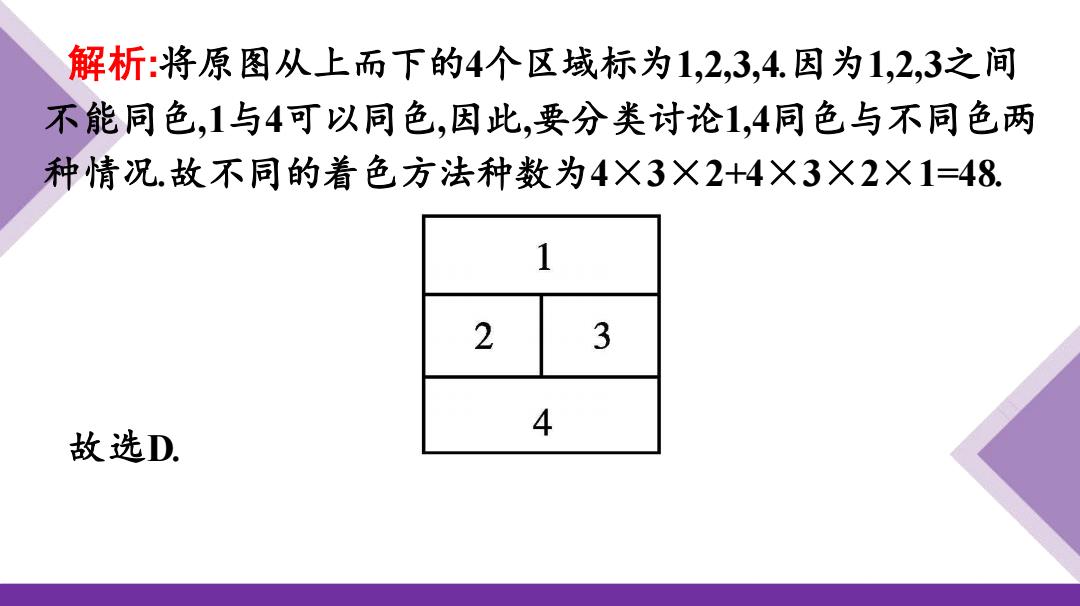
解析:将原图从上而下的4个区域标为1,2,3,4.因为1,2,3之间 不能同色,1与4可以同色,因此,要分类讨论1,4同色与不同色两 种情况.故不同的着色方法种数为4×3×2+4×3×2×1=48. 故选D

命题角度2:“步中有类”的计数问题 【典型例题2】有4名同学在同一天的上、下午参加“身高 与体重”“立定跳远“肺活量“握力“台阶”五个项目的测试, 每名同学上、下午各测试一个项目,且不重复若上午不测“握 力”项目,下午不测“台阶”项目,其余项目上、下午都各测一人, 则不同的安排方式共有 种.(用数字作答) 答案:264
命题角度2:“步中有类”的计数问题 【典型例题2】有4名同学在同一天的上、下午参加“身高 与体重”“立定跳远”“肺活量”“握力”“台阶”五个项目的测试, 每名同学上、下午各测试一个项目,且不重复.若上午不测“握 力”项目,下午不测“台阶”项目,其余项目上、下午都各测一人, 则不同的安排方式共有 种.(用数字作答) 答案:264

解析:上午总测试方法有4X3X2X1=24种;以A,B,C,D,E依 次代表五个测试项目.若上午测试E的同学下午测试D,则上午 测试A的同学下午只能测试B,C,确定上午测试A的同学后其 余两名同学上、下午的测试方法共有2种;若上午测试E的同 学下午测试A,B,C之一,则上午测试A,B,C中任何一个的同学 下午都可以测试D,安排完这名同学后其余两名同学的测试方 式就确定了,故共有3×3=9种测试方法,即下午的测试方法共 有11种.根据分步乘法计数原理,总的测试方法共有 24×11=264种
解析:上午总测试方法有4×3×2×1=24种;以A,B,C,D,E依 次代表五个测试项目.若上午测试E的同学下午测试D,则上午 测试A的同学下午只能测试B,C,确定上午测试A的同学后其 余两名同学上、下午的测试方法共有2种;若上午测试E的同 学下午测试A,B,C之一,则上午测试A,B,C中任何一个的同学 下午都可以测试D,安排完这名同学后其余两名同学的测试方 式就确定了,故共有3×3=9种测试方法,即下午的测试方法共 有11种.根据分步乘法计数原理,总的测试方法共有 24×11=264种