
全程设计 5.2 导数的运算 5.2.1 基本初等函数的导数
5.2 导数的运算 5.2.1 基本初等函数的导数
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随 堂 训 练

导航 素养·目标定位 目标素养 L.能根据导数的定义求函数=cJ=xJ=xJ-x,=V的导 数,提升逻辑推理核心素养 2.能利用给出的基本初等函数的导数公式求简单函数的导数, 提升数学运算核心素养
导航 目 标 素 养 1.能根据导数的定义求函数y=c,y=x,y=x2 ,y=x3 , 的导 数,提升逻辑推理核心素养. 2.能利用给出的基本初等函数的导数公式求简单函数的导数, 提升数学运算核心素养. 素养·目标定位 y= 𝟏 𝐱 ,y= 𝐱
知识概览 导航 几个常用函数 基本初等函 的导数 数的导数 基本初等函数 的导数公式
知 识 概 览 导航
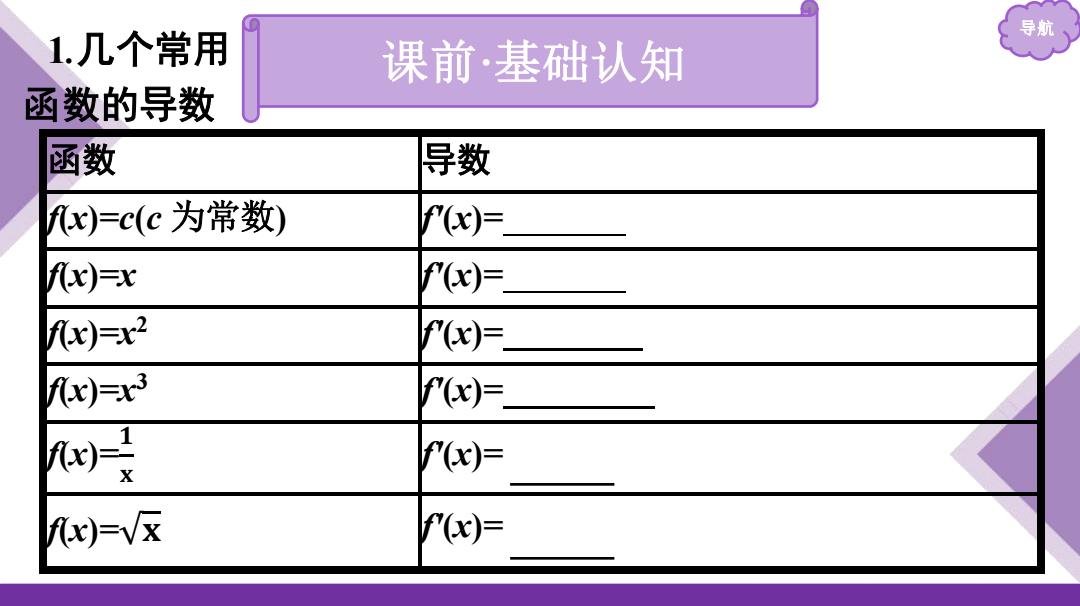
1.几个常用 导航 课前·基础认知 函数的导数 函数 导数 fx)=c(c为常数) f(x)= fx)=x f(x)= )=x2 f"(x)= x)=x3 f(x)=. 月 f(x)= fx)=/x )=
导航 1 .几个常用 函数的导数 函数 导数 f(x)=c(c 为常数) f'(x)= 0 f(x)=x f'(x)= 1 f(x)=x2 f'(x)= 2x f(x)=x3 f'(x)= 3x2 f(x)=𝟏𝐱 f'(x)= - 𝟏𝐱𝟐 f(x)= 𝐱 f'(x)= 𝟏𝟐 𝐱 课前 ·基础认知

2.基本初等函数的导数公式 导航、 函数 导数 x)=c(c为常数) f"(x)= fx)=x(a∈Q,且a0) fx)=」 f(x)=sin x f(x)= fx)=cosx f(x)= fx)=(a>0,且味1) f(x)= f)=e' f(x)= f)=logx(a>0,且呋1) f(x)= fx)=In x f"(x)=
导航 2 .基本初等函数的导数公式 函数 导数 f(x)=c(c 为常数) f'(x)= 0 f(x)=xα(α∈Q,且 α≠0) f'(x)= αxα-1 f(x)=sin x f'(x)= cos x f(x)=cos x f'(x)= -sin x f(x)=ax(a>0,且 a≠1) f'(x)= ax ln a f(x)=ex f'(x)= ex f(x)=logax(a>0,且 a≠1) f'(x)= 𝟏𝐱𝒍𝒏𝐚 f(x)=ln x f'(x)= 𝟏𝐱

导航 微训练函数y=gx的导数为 答案y1 xIn10
导航 微训练 函数y=lg x的导数为 . 答案:y'= 𝟏 𝒙𝐥𝐧𝟏𝟎

导航 课堂·重难突破 利用求导公式求常见的基本初等函数的导数 典例剖析 1.求下列函数的导数: ((I3(2-og2x:3y=c0s(4=2
导航 一 利用求导公式求常见的基本初等函数的导数 典例剖析 1.求下列函数的导数: 课堂·重难突破 (1)y= 𝟏 𝒙 𝟓 ;(2)y=lo𝐠𝟏 𝟐 x;(3)y=cos 𝛑 𝟒 ;(4)y=2 2x

导航 解(1p()t=-5=5 1 3p=(cos9)0. (4).y=22x=4,.y'=(49)=4n4
导航 解:(1)y'= 𝟏 𝒙 𝟓 '=(x -5 )'=-5x -6 =- 𝟓 𝒙 𝟔 . (2)y'= 𝟏 𝒙𝐥𝐧 𝟏 𝟐 =- 𝟏 𝒙𝐥𝐧𝟐 . (3)y'= 𝐜𝐨𝐬 𝛑 𝟒 '=0. (4)∵y=2 2x =4 x ,∴y'=(4x )'=4 x ln 4

规律总结1.若给出的函数符合基本初等函数的导数公式的 形式,则直接利用公式求导 2.若给出的函数不符合基本初等函数的导数公式的形式,则 通过恒等变换对函数解析式进行化简或变形后求导.如y=Vxm m,n∈N心1)需先化为=品是需先化为=
导航 规律总结 1.若给出的函数符合基本初等函数的导数公式的 形式,则直接利用公式求导. 2.若给出的函数不符合基本初等函数的导数公式的形式,则 通过恒等变换对函数解析式进行化简或变形后求导.如 y= 𝒏 𝒙 𝒎 (m,n∈N * ,n>1)需先化为 y=𝒙 𝒎 𝒏 ,y= 𝟏 𝒙 𝒂 需先化为 y=x-a