
全程设计 4.3.2等比数列的前n项和公式 第2课时 等比数列前n须和的性质及 应用
4.3.2 等比数列的前n项和公式 第2课时 等比数列前n项和的性质及 应用
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随 堂 训 练

导期 素养·目标定位 目标素养 L.掌握等比数列的前项和的性质的应用.通过等比数列的前 n项和性质的学习,提升逻辑推理素养. 2.掌握等差数列与等比数列的综合应用,提升数据分析素养 3.能运用等比数列的前项和公式解决一些简单的实际问题, 提升数学建模素养
导航 目 标 素 养 1.掌握等比数列的前n项和的性质的应用.通过等比数列的前 n项和性质的学习,提升逻辑推理素养. 2.掌握等差数列与等比数列的综合应用,提升数据分析素养. 3.能运用等比数列的前n项和公式解决一些简单的实际问题, 提升数学建模素养. 素养·目标定位
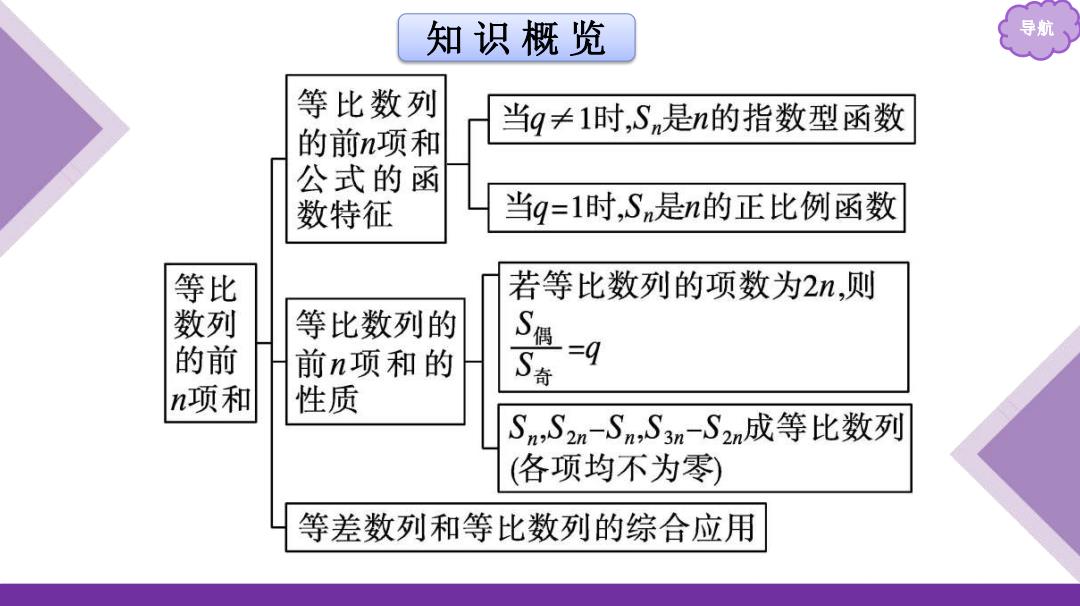
知识概览 导航 等比数列 当g≠1时,Sn是n的指数型函数 的前n项和 公式的函 数特征 当q=1时,Sm是n的正比例函数 等比 若等比数列的项数为2n,则 数列 等比数列的 的前 前n项和的 S奇 n项和 性质 Sm,S2n-Sn,S3m-S2n成等比数列 (各项均不为零) 等差数列和等比数列的综合应用
知 识 概 览 导航

导 课前·基础认知 1.等比数列的前项和公式的函数特征 当公比1时,等比数列的前n项和公式是S,11g它可以 1-q 变形为S8品品设A品则上式可写成S 由此可见,当公比g≠1时,等比数列的前n项和Sn是由关于n的 一个指数式与一个常数的和构成的,而指数式的系数与常数 项互为相反数当公比q=1时,因为a10,所以Sm=na1是n的正比 例函数(常数项为0的一次函数)
导航 1.等比数列的前n项和公式的函数特征 当公比 q≠1 时,等比数列的前 n 项和公式是 Sn= 𝒂𝟏(𝟏-𝒒 𝒏) 𝟏-𝒒 ,它可以 变形为 Sn=- 𝒂𝟏 𝟏-𝒒 ·q n + 𝒂𝟏 𝟏-𝒒 ,设 A= 𝒂𝟏 𝟏-𝒒 ,则上式可写成 Sn= -Aqn +A . 由此可见,当公比q≠1时,等比数列的前n项和Sn是由关于n的 一个指数式与一个常数的和构成的,而指数式的系数与常数 项互为相反数.当公比q=1时,因为a1≠0,所以Sn=na1是n的正比 例函数(常数项为0的一次函数). 课前·基础认知

导航 微探究在数列{a,}中,t1=can(c为非零常数),且前n项和 Sn=3-l+k,则实数k的值是什么? 提示:由题意知{am}是等比数列,即3的系数与常数项互为相 反数,而3”的系数为,故仁骨
导航 微探究 在数列{an }中,an+1=can (c为非零常数),且前n项和 Sn =3 n-1+k,则实数k的值是什么? 提示:由题意知{an }是等比数列,即3 n的系数与常数项互为相 反数, 而 3 n 的系数为𝟏 𝟑 ,故 k=- 𝟏 𝟑

2.等比数列的前n项和的性质 导 ()若数列{a}是公比不为-1的等比数列Sn为其前n项和,则 SnS2 SS3mS2n,…仍构成等比数列. (2)若{an}是公比为q的等比数列,则SHm=Sn+qSm(n,m∈N 3)若{an}是公比为q的等比数列,S偶S奇分别是数列的偶数项 和与奇数项和,则: ①在其前2n项中s有 0的 ②在其前2n+1项中, S奇-S偶=01-l2十l3-4十-2n十l2n+1 a1+a2n+19 = 1-(q) antazntz(gf-1). 1+q
导航 2.等比数列的前n项和的性质 (1)若数列{an }是公比不为-1的等比数列,Sn为其前n项和,则 Sn ,S2n -Sn ,S3n -S2n , …仍构成等比数列. (2)若{an }是公比为q的等比数列,则Sn+m =Sn+qnSm(n,m∈N* ). (3)若{an }是公比为q的等比数列,S偶,S奇分别是数列的偶数项 和与奇数项和,则: ①在其前 2n 项中, 𝑺 偶 𝑺 奇 =q; ②在其前 2n+1 项中, S 奇-S 偶=a1-a2+a3-a4+…-a2n+a2n+1= 𝒂𝟏 +𝒂𝟐𝒏+𝟏 𝒒 𝟏-(-𝒒) = 𝒂𝟏 +𝒂𝟐𝒏+𝟐 𝟏+𝒒 (q≠-1)

导航 微训练在等比数列{an}中,若a1+2=20,43+a4=40,如何求S6的 值? 提示:由S2=20,S4-S2=40,得S6-S4=80, 故S6=S4+80=S2+40+80=140
导航 微训练 在等比数列{an }中,若a1+a2 =20,a3+a4 =40,如何求S6的 值? 提示:由S2 =20,S4 -S2 =40,得S6 -S4 =80, 故S6=S4+80=S2+40+80=140

导航 课堂·重难突破 等比数列的前n项和的性质 典例剖析 1.已知等比数列{an}的前n项和Sn=48,前2n项和S2m=60,则前 3n项和S3mF 答案:63
导航 一 等比数列的前n项和的性质 典例剖析 1.已知等比数列{an }的前n项和Sn =48,前2n项和S2n =60,则前 3n项和S3n = . 答案:63 课堂·重难突破

解析:(方法一)设等比数列{}的公比为,由题意可知1, 7a11-q=48, 得 1-q gn=1 a11-g2 → 2=60 a1= 1-q 1-q 64, 故5=告4-64(1)63 1-q (方法二)由题意可知SmS2 -SS3nS2n成等比数列, 得(S2mSm)2=Sm(S3mS2m),即(60-48)2=48(S3m60), 故S3m=63
导航 解析:(方法一)设等比数列{an }的公比为q,由题意可知q≠1, 得 𝒂𝟏(𝟏-𝒒 𝒏) 𝟏-𝒒 = 𝟒𝟖, 𝒂𝟏(𝟏-𝒒 𝟐𝒏) 𝟏-𝒒 = 𝟔𝟎 ⇒ 𝒒 𝒏 = 𝟏 𝟒 , 𝒂𝟏 𝟏-𝒒 = 𝟔𝟒, 故 S3n= 𝒂𝟏(𝟏-𝒒 𝟑𝒏) 𝟏-𝒒 = 𝒂𝟏 𝟏-𝒒 ·[1-(q n ) 3 ]=64× 𝟏- 𝟏 𝟔𝟒 =63. (方法二)由题意可知Sn ,S2n -Sn ,S3n -S2n成等比数列, 得(S2n -Sn ) 2=Sn·(S3n -S2n ),即(60-48)2=48(S3n -60). 故S3n =63