
全程设计 2.2.1 不等式及其性质 第1课时 不等式的性质
2.2.1 不等式及其性质 第1课时 不等式的性质
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航 课标定位素养阐释 1.了解现实世界和日常生活中的不等关系. 2.掌握不等式的性质. 3.了解作差法,能够利用不等式的性质进行数和式的大小比较 4.注重逻辑推理能力和数学运算能力的培养
导航 课标定位素养阐释 1.了解现实世界和日常生活中的不等关系. 2.掌握不等式的性质. 3.了解作差法,能够利用不等式的性质进行数和式的大小比较. 4.注重逻辑推理能力和数学运算能力的培养

导期 课前·基础认知 不等式的概念 【问题思考】 1.小明的身高是xcm,妈妈的身高是162cm,爸爸的身高是180 cm.已知小明比妈妈高,但他不高于爸爸,则x应满足什么关系? 提示:162<x≤180. 2.填空:用数学符号 连接两个数或代数 式,以表示它们之间的不等关系,含有这些 的式子,称为 不等式
导航 课前·基础认知 一、不等式的概念 【问题思考】 1.小明的身高是x cm,妈妈的身高是162 cm,爸爸的身高是180 cm.已知小明比妈妈高,但他不高于爸爸,则x应满足什么关系? 提示:162”“<”“≥”“≤” 连接两个数或代数 式,以表示它们之间的不等关系,含有这些不等号的式子,称为 不等式

导航、 3.“0≥0”成立吗?为什么? 提示:成立.0≥0台0>0或0=0,由0=0成立,得0≥0成立
导航 3.“0≥0”成立吗?为什么? 提示:成立.0≥0⇔0>0或0=0,由0=0成立,得0≥0成立
4如图,在日常生活中,我们经常看到下列标志: 导月 其含义分别为: ①最低限速:限制行驶时速不得低于 50 km/h; 50 10t 3.5m ② 限制质量:装载总质量m不得超过10t; ① ③限制高度:装载高度h不得超过3.5m; ④限制宽度:装载宽度a不得超过3m; 7:30-10:00 ⑤时间范围:t∈7.5,10. ④ ⑤ 你能用数学式子表示上述关系吗? 解:①v≥50;②m≤10;③h≤3.5;④a≤3;⑤7.5≤t≤10
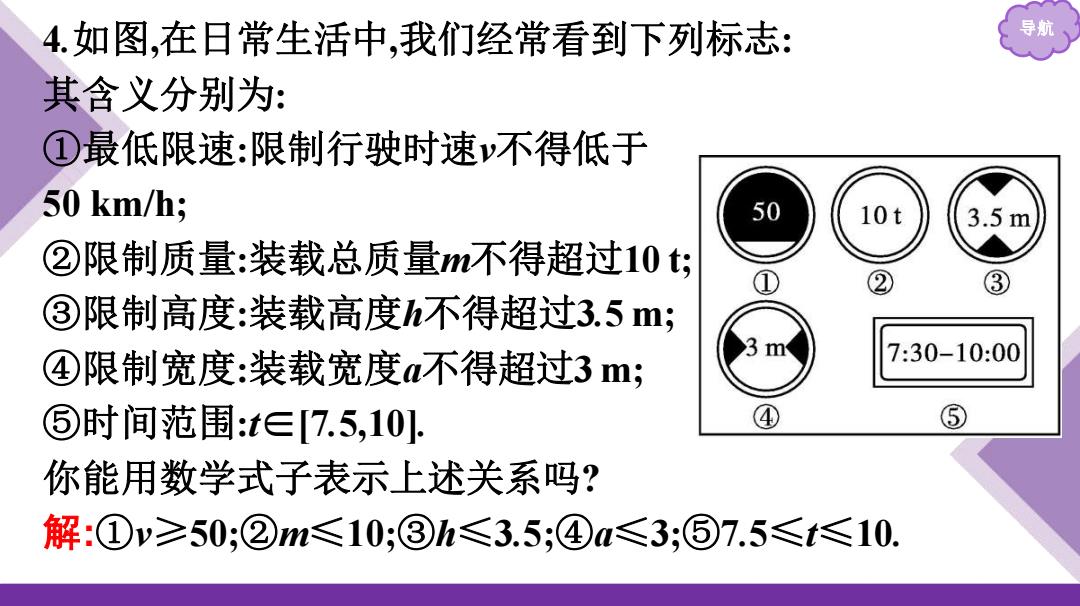
导航 4.如图,在日常生活中,我们经常看到下列标志: 其含义分别为: ①最低限速:限制行驶时速v不得低于 50 km/h; ②限制质量:装载总质量m不得超过10 t; ③限制高度:装载高度h不得超过3.5 m; ④限制宽度:装载宽度a不得超过3 m; ⑤时间范围:t∈[7.5,10]. 你能用数学式子表示上述关系吗? 解:①v≥50;②m≤10;③h≤3.5;④a≤3;⑤7.5≤t≤10

导航 二、 用作差法赴比较大小 【问题思考】 1.已知表示实数a和b的两个点分别为A,B,则当点A,B重合时; 点A在点B的右侧时;点A在点B的左侧时,与b的大小关系分 别是什么? 提示:=b;心b;a<b
导航 二、用作差法比较大小 【问题思考】 1.已知表示实数a和b的两个点分别为A,B,则当点A,B重合时; 点A在点B的右侧时;点A在点B的左侧时,a与b的大小关系分 别是什么? 提示:a=b;a>b;a<b

导 2.填空:要比较两个实数,b的大小,只要考查a-b与0的相对大 小就可以了, 即-b0←台 3.通过比较两式之差的符号来判断两式的大小,这种方法通常 称为
导航 2.填空:要比较两个实数a,b的大小,只要考查a-b与0的相对大 小就可以了, 即a-b0⇔ a>b . 3.通过比较两式之差的符号来判断两式的大小,这种方法通常 称为作差法

导航 4.做一做:已知M=x23x+7,N=-x2+x+1,则( A.M0∴.M>N 答案:B
导航 4.做一做:已知M=x2 -3x+7,N=-x 2+x+1,则( ) A.MN C.M=N D.无法判断 解析:∵M-N=(x 2 -3x+7)-(-x 2+x+1)=2(x-1)2+4>0,∴M>N. 答案:B

导航 三、不等式的性质 【问题思考】 1.由>b能否得到a+m>b+m?am>bm呢?2>b2呢? 提示:由>b可以得到a+m>b+m,但不一定能得到am>bm和 a2>b2
导航 三、不等式的性质 【问题思考】 1.由a>b能否得到a+m>b+m?am>bm呢?a 2>b2呢? 提示:由a>b可以得到a+m>b+m,但不一定能得到am>bm和 a 2>b2