
全程设计 3.4 数学建模活动:决定苹果的最佳出 鲁时间点
3.4 数学建模活动:决定苹果的最佳出 售时间点

课标定位素养阐释 1.了解数学建模的意义 2.了解数学建模的基本过程 3.能够运用已有函数模型或建立函数模型解决实际问题 4.经历数学建模的全过程,提升数学建模、数学抽象、数据分 析、数学运算、逻辑推理和直观想象素养
课标定位素养阐释 1.了解数学建模的意义. 2.了解数学建模的基本过程. 3.能够运用已有函数模型或建立函数模型解决实际问题. 4.经历数学建模的全过程,提升数学建模、数学抽象、数据分 析、数学运算、逻辑推理和直观想象素养

数学建模简介 1.数学建模的概念 对现实问题进行数学抽象,用数学语言表达问题、用数学方 法构建模型解决问题的素养就是数学建模
一、数学建模简介 1.数学建模的概念 对现实问题进行数学抽象,用数学语言表达问题、用数学方 法构建模型解决问题的素养就是数学建模

2.数学建模的过程 发现问题提出问题一根据现实生活和生产的实际情况,切 合问题的实际背景,发现需要解决的问题,提出具有实际意义 的问题 火 分析问题建立模型 一在分析实际问题的基础上,利用适当 的数学工具来刻画各变量、常量之间的数学关系,建立相应 的数学模型(尽量用简单的数学模型)
2.数学建模的过程 发现问题提出问题——根据现实生活和生产的实际情况,切 合问题的实际背景,发现需要解决的问题,提出具有实际意义 的问题 ↓ 分析问题建立模型——在分析实际问题的基础上,利用适当 的数学工具来刻画各变量、常量之间的数学关系,建立相应 的数学模型(尽量用简单的数学模型) ↓

确定参数计算求解一 利用调查研究获取的数据资料,把数 据代入数学模型进行计算,求出参数的值(或近似值) 验证结果改进模型 将模型分析结果与实际情形进行比较, 以此来验证模型的准确性、合理性和适用性.如果模型与实 际较吻合,则要对计算结果给出其实际含义,并进行解释如果 模型与实际吻合较差,则应该修改假设,再次重复建模过程对 模型进行改进
确定参数计算求解——利用调查研究获取的数据资料,把数 据代入数学模型进行计算,求出参数的值(或近似值) ↓ 验证结果改进模型——将模型分析结果与实际情形进行比较, 以此来验证模型的准确性、合理性和适用性.如果模型与实 际较吻合,则要对计算结果给出其实际含义,并进行解释.如果 模型与实际吻合较差,则应该修改假设,再次重复建模过程对 模型进行改进
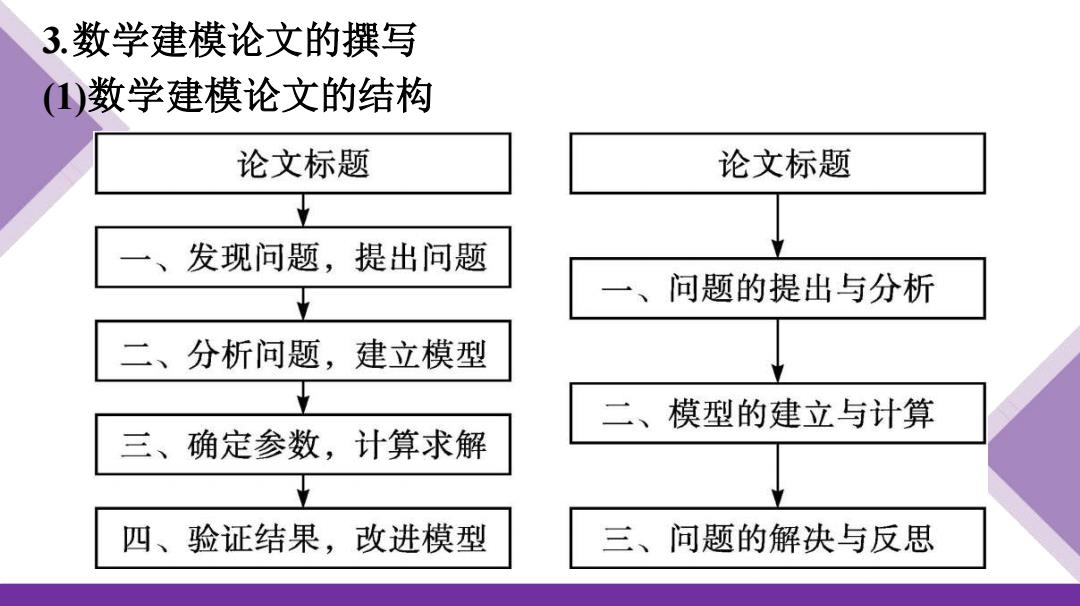
3.数学建模论文的撰写 ()数学建模论文的结构 论文标题 论文标题 发现问题,提出问题 一、问题的提出与分析 二、分析问题,建立模型 二、模型的建立与计算 三、确定参数,计算求解 四、验证结果,改进模型 三、问题的解决与反思
3.数学建模论文的撰写 (1)数学建模论文的结构
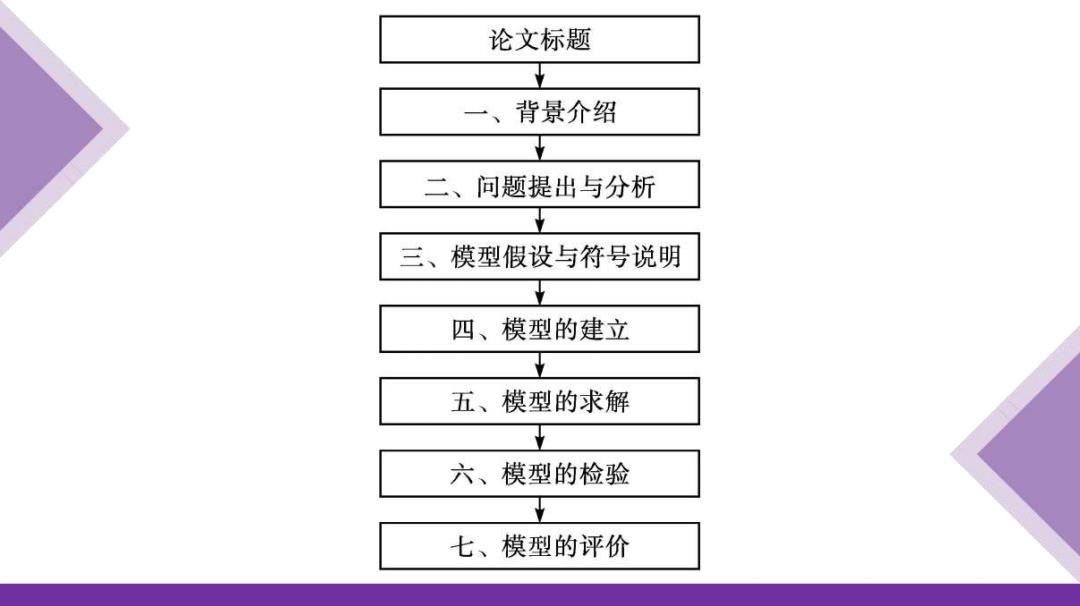
论文标题 一、背景介绍 二、问题提出与分析 三、模型假设与符号说明 】 四、模型的建立 】 五、模型的求解 六、模型的检验 五 七、模型的评价

(2)撰写数学建模论文的要求 ①数学建模的过程中,往往采用分工合作的方式进行, ②一个数学建模小组由3一5人组成理想的小组中,既要有数 学基础扎实的同学,也要有能熟练使用计算机的同学,还要有 写作表达能力强的同学
(2)撰写数学建模论文的要求 ①数学建模的过程中,往往采用分工合作的方式进行. ②一个数学建模小组由3—5人组成.理想的小组中,既要有数 学基础扎实的同学,也要有能熟练使用计算机的同学,还要有 写作表达能力强的同学

二、建立函数模型解决实际问题实例 1利用已有函数模型解决实际问题 【典例1】汽车在行驶中,由于惯性的作用,刹车后还要继续 向前滑行一段距离才能停止,我们称这段距离为“刹车距离” 刹车距离是分析事故原因的一个重要因素.在一个限速为40 k/h的弯道上,甲、乙两辆汽车相向而行,发现情况不对,同时 刹车,但还是相碰了.事后现场勘查测得甲车的刹车距离略超 过12m,乙车的刹车距离略超过10m,又知甲、乙两种车型的 刹车距离s(单位:m)与车速x(单位:km/h)之间分别有如下关 系:s甲=0.1x+0.01x2,sz=0.05x0.005x2.试判断甲、乙两车有无 超速现象,并根据所学数学知识给出判断的依据
二、建立函数模型解决实际问题实例 1.利用已有函数模型解决实际问题 【典例1】汽车在行驶中,由于惯性的作用,刹车后还要继续 向前滑行一段距离才能停止,我们称这段距离为“刹车距离” . 刹车距离是分析事故原因的一个重要因素.在一个限速为40 km/h的弯道上,甲、乙两辆汽车相向而行,发现情况不对,同时 刹车,但还是相碰了.事后现场勘查测得甲车的刹车距离略超 过12 m,乙车的刹车距离略超过10 m,又知甲、乙两种车型的 刹车距离s(单位:m)与车速x(单位:km/h)之间分别有如下关 系:s甲=0.1x+0.01x 2 ,s乙=0.05x+0.005x 2 .试判断甲、乙两车有无 超速现象,并根据所学数学知识给出判断的依据

分析:根据已经给出的刹车距离与车速的函数关系,由刹车距 离建立不等式,求出两辆车的车速范围,然后进行判断 解:依题意可得,甲车的刹车距离s甲=0.1x+0.01x2>12, 即x2+10x-1200>0,解得x>30或x10,即x2+10x-2000>0, 解得x>40或x<-50(不合实际意义,舍去), 这表明乙车的车速超过40km/h,超过规定限速 综上所述,甲车没有超速现象,乙车有超速现象
分析:根据已经给出的刹车距离与车速的函数关系,由刹车距 离建立不等式,求出两辆车的车速范围,然后进行判断. 解:依题意可得,甲车的刹车距离s甲=0.1x+0.01x 2>12, 即x 2+10x-1 200>0,解得x>30或x10,即x 2+10x-2 000>0, 解得x>40或x<-50(不合实际意义,舍去), 这表明乙车的车速超过40 km/h,超过规定限速. 综上所述,甲车没有超速现象,乙车有超速现象