
全程设计 7.3.3 余弦函数的性质与图象
7.3.3 余弦函数的性质与图象

导航 课标定位 素养阐释 1.了解余弦函数的定义 2.会作余弦函数的图象 3.了解余弦函数的有关性质 4.加强直观想象、逻辑推理、数学运算能力的培养
导航 课标定位 素养阐释 1.了解余弦函数的定义. 2.会作余弦函数的图象. 3.了解余弦函数的有关性质. 4.加强直观想象、逻辑推理、数学运算能力的培养
课前·基础认知 课堂·重难突破 随堂训练 易错辨析
易 错 辨 析 课前·基础认知 课堂·重难突破 随 堂 训 练

导航 课前·基础认知 余弦函数的性质与图象 【问题思考】 1.对于任意一个角x,cosx有几个值与之对应? 提示:一个 2.由y=sinx,x∈R的图象如何得到y=cosx,x∈R的图象? 提示:把y=sinx的图象向左平移个单位,得到sin(x+罗 的图像,即y=C0sx的图象
导航 课前·基础认知 余弦函数的性质与图象 【问题思考】 1.对于任意一个角x,cos x有几个值与之对应? 提示:一个. 2.由y=sin x,x∈R的图象如何得到y=cos x,x∈R的图象? 提示:把 y=sin x 的图象向左平移𝛑 𝟐 个单位,得到 y=sin 𝒙 + 𝛑 𝟐 的图像,即 y=cos x 的图象

导航 3.填空:(1)函数y=cosx,∈R称为余弦函数y=cosx的图象称 为余弦曲线 (2)余弦函数的性质: 函数 V-COS x 定义域 R 值域 奇偶性 函数 周期性 以为周期(k∈Z,0),为最小正周期
导航 3.填空:(1)函数y=cos x,x∈R称为余弦函数,y=cos x的图象称 为余弦曲线. (2)余弦函数的性质: 函数 y=cos x 定义域 R 值域 [-1,1] 奇偶性 偶函数 周期性 以 2kπ 为周期(k∈Z,k≠0),2π 为最小正周期

导航、 函数 y-cos x 单调性 当x∈ 时,单调递增; 当x∈ 时,单调递减 最大值与 当x=(k∈Z时,最大值为_, 最小值 当x= (k∈Z时,最小值为 零点 kx= ,k∈Z 对称轴 x=,k∈Z 对称中心 g+km,0),k∈Z
导航 函数 y=cos x 单调性 当 x∈[2kπ-π,2kπ](k∈Z)时,单调递增; 当 x∈[2kπ,2kπ+π](k∈Z)时,单调递减 最大值与 最小值 当 x=2kπ(k∈Z)时,最大值为 1; 当 x=2kπ+π(k∈Z)时,最小值为-1 零点 x=kπ+ 𝜋 2 ,k∈Z 对称轴 x=kπ,k∈Z 对称中心 π 2 + 𝑘π,0 ,k∈Z

导航 4.做一做:(1)y=3cosx+5的最大值是 2)函数=1-2c0s(2x+罗)的周期为 (3)函数fx)=cos xsin x是 函数(填“奇”或“偶). 答案:(1)8(2)m(3)奇
导航 4.做一做:(1)y=3cos x+5的最大值是 ; (2)函数 y=1-2cos 𝟐𝒙 + 𝛑 𝟑 的周期为 ; (3)函数f(x)=cos xsin x是 函数(填“奇”或“偶”). 答案:(1)8 (2)π (3)奇

【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√”,错 误的画“X” ()余弦函数y=c0sx是偶函数,其图象关于y轴对称,对称轴有 无数多条.() (2)余弦函数y=C0sx的图象是轴对称图形,也是中心对称图形, (3)在区间0,3π上,函数y=c0sx仅在x=0时取得最大值1.( (4)函数y=cosx在区间2可上是减函数.() (⑤)函数y=c0sx,x∈0,10π是周期函数,最小正周期为2元.(
【思考辨析】 导航 判断下列说法是否正确,正确的在它后面的括号里画“√”,错 误的画“×” . (1)余弦函数y=cos x是偶函数,其图象关于y轴对称,对称轴有 无数多条.( √ ) (2)余弦函数y=cos x的图象是轴对称图形,也是中心对称图形. ( √ ) (3)在区间[0,3π]上,函数y=cos x仅在x=0时取得最大值1.( × ) (4)函数y=cos x在区间 上是减函数.( √ ) (5)函数y=cos x,x∈[0,10π]是周期函数,最小正周期为2π.( × ) 𝛑 𝟐 ,𝛑

导航 课堂·重难突破 探究一用“五点法”作余弦型函数的图象 【例1】用“五点法”作函数y=2+c0sx,∈[0,2π的简图. 分析:在区间[0,2π上描出五个关键点,用平滑的曲线连接即可
导航 课堂·重难突破 探究一 用“五点法”作余弦型函数的图象 【例1】用“五点法”作函数y=2+cos x,x∈[0,2π]的简图. 分析:在区间[0,2π]上描出五个关键点,用平滑的曲线连接即可
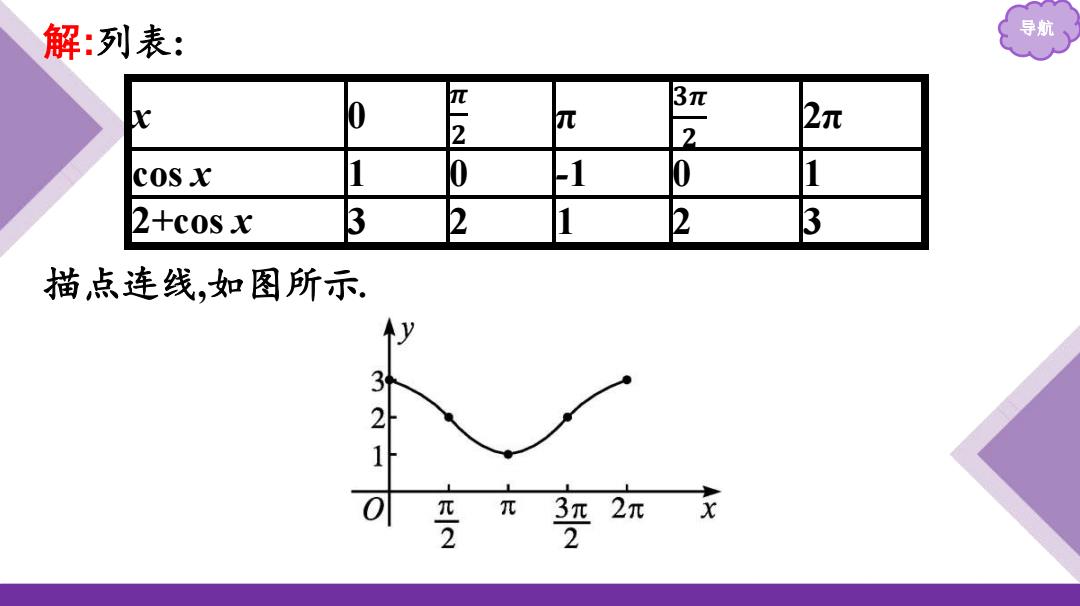
解:列表: 导航 0 3π 2 元 2. 2元 COSx 1 0 1 0 1 2+cos x 3 2 1 2 3 描点连线,如图所示 个y 3 1 0 π2 π3π2π 2
导航 解:列表: x 0 𝝅 𝟐 π 𝟑𝝅 𝟐 2π cos x 1 0 -1 0 1 2+cos x 3 2 1 2 3 描点连线,如图所示