
全程设计 第四章 指数函数、对数函数与幂函数 4.1.2 指数函数的性质与图象 第1课时 指数丞数的性质与图象
第四章 指数函数、对数函数与幂函数 4.1.2 指数函数的性质与图象 第1课时 指数函数的性质与图象

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导期 课前·基础认知 指数函数的概念 【问题思考】 1.(1)细胞分裂时,经过一次分裂,一个细胞变为两个细胞;经过 两次分裂,变为四个细胞;经过三次分裂,变为八个细胞..若 开始时只有一个细胞,经过x次分裂,细胞个数为y,则x与y的关 系式是怎样的? (2)y=x2和y=2都是指数函数吗? 提示:(1y=2x,x∈N(2)y=2r是指数函数
导航 课前·基础认知 一、指数函数的概念 【问题思考】 1.(1)细胞分裂时,经过一次分裂,一个细胞变为两个细胞;经过 两次分裂,变为四个细胞;经过三次分裂,变为八个细胞……若 开始时只有一个细胞,经过x次分裂,细胞个数为y,则x与y的关 系式是怎样的? (2)y=x2和y=2 x都是指数函数吗? 提示:(1)y=2 x ,x∈N+ . (2)y=2 x是指数函数

2.填空:一般地,函数 称为指数函数,其中a是常数,心0且 味1. 3指数函数y=(a>0,呋1)的定义域是什么? 提示:当心>0时x是任意一个实数时,都是一个确定的实数,故 函数的定义域为实数集R 4.为何规定底数大于0且不等于1? 提示:如果M=0,当x>0时,恒等于0,当x≤0时,心无意义;如果 0,叶1
导航 2.填空:一般地,函数y=ax 称为指数函数,其中a是常数,a>0且 a≠1. 3.指数函数y=ax (a>0,a≠1)的定义域是什么? 提示:当a>0时,x是任意一个实数时,a x都是一个确定的实数,故 函数的定义域为实数集R. 4.为何规定底数a大于0且不等于1? 提示:如果a=0,当x>0时,a x恒等于0,当x≤0时,a x无意义;如果 a0,a≠1. 𝟏 𝟒 𝟏 𝟐

导航 5.指数函数解析式y=(>0,呋1)有何结构特征? 提示:(1)的系数是1;2)指数上只有自变量x3)底数a是大于 0且不等于1的常数
导航 5.指数函数解析式y=ax (a>0,a≠1)有何结构特征? 提示:(1)a x的系数是1;(2)指数上只有自变量x;(3)底数a是大于 0且不等于1的常数

导航 二、指数函数的图象和性质 【问题思考】 1.怎样作出函数y=2x的图象? 提示:描点法 2.函数y=心与=(得)(>0,且味1)的图象有何关系? 提示:关于轴对称
导航 二、指数函数 的图象 和性质 【问题思考】 1 .怎样作出函数y= 2 x 的图象 ? 提示 :描点法 . 2.函数 y=ax 与 y= 𝟏𝒂 𝒙(a>0, 且 a ≠1)的图 象有何关系? 提示 :关于y轴对称
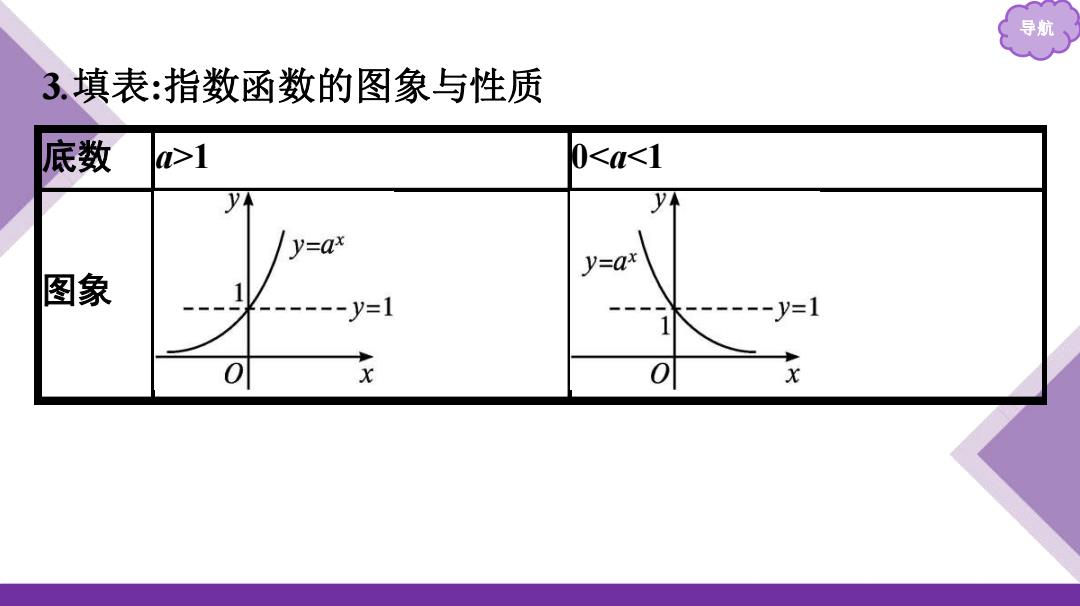
导航 3.填表:指数函数的图象与性质 底数 >1 0<a<1 y y不 y=ax y=ax 图象 ------y=1 1 -----y=1 0 x 0 x
导航 3 .填表 :指数函数 的图象与性质 底数 a>1 0<a<1 图象

底数 a>1 00时, 当>0时, 当x<0时: 当x<0时, 既不是奇函数,也不是偶函数
导航 底数 a>1 00 时,y>1; 当 x0 时,01 既不是奇函数,也不是偶函数

导航 4.做一做: ()函数y=51的值域为 (2)函数fx)=-2+2(>0,味1)的图象过定点 (3)若函数gx)=(2m-1)r是减函数,则实数的取值范围 是 答案:(1)-1,+o)(22,3)(3)((,1)
导航 4.做一做: (1)函数y=5 x -1的值域为 ; (2)函数f(x)=ax-2+2(a>0,a≠1)的图象过定点 ; (3)若函数g(x)=(2m-1)x是减函数,则实数m的取值范围 是 . 答案:(1)(-1,+∞) (2)(2,3) (3) 𝟏 𝟐 ,𝟏

导航 课堂·重难突破 探究一指数型函数的定义域、值域 【例1】求下列函数的定义域和值域; (2,(2=V1-2;(3( x2.2x-3 分析:根据函数解析式有意义可求定义域;由定义域确定值域
导航 课堂·重难突破 探究一 指数型函数的定义域、值域 【例1】求下列函数的定义域和值域; (1)y=𝟐 𝟏 𝒙-𝟒;(2)y= 𝟏-𝟐𝒙;(3)y= 𝟏 𝟐 𝒙 𝟐 -𝟐𝒙-𝟑 . 分析:根据函数解析式有意义可求定义域;由定义域确定值域