
全程设计 7.3.5 已知三角函数值求角
7.3.5 已知三角函数值求角

导 课标定位 素养阐释 1掌握已知三角函数值求角的方法,并能根据已知的三角函数 值求角. 2.能用符号arcsinx,arccos七,arctanx.表示角. 3.加强数学抽象、直观想象、数学运算能力的培养
导航 课标定位 素养阐释 1.掌握已知三角函数值求角的方法,并能根据已知的三角函数 值求角. 2.能用符号arcsin x,arccos x,arctan x表示角. 3.加强数学抽象、直观想象、数学运算能力的培养
课前·基础认知 课堂·重难突破 随堂训练 易错辨析
易 错 辨 析 课前·基础认知 课堂·重难突破 随 堂 训 练

导 课前·基础认知 已知正弦值求角 【问题思考】 1.函数y=sinx,x∈Ry∈[-1,1],对任一x值,有几个y值与之对应? 对于任一y值,有几个x值与之对应? 提示:一个;无数个 2.对于函数=sinx,x∈[,引y∈-1,,对于任一值,有多少 个x值与之对应? 提示:一个
导航 课前·基础认知 一、已知正弦值求角 【问题思考】 1.函数y=sin x,x∈R,y∈[-1,1],对任一x值,有几个y值与之对应? 对于任一y值,有几个x值与之对应? 提示:一个;无数个. 2.对于函数y=sin x, ,y∈[-1,1],对于任一y值,有多少 个x值与之对应? 提示:一个. x∈ - 𝛑 𝟐 , 𝛑 𝟐

导期 3填空:任意给定一个y∈-1,1,当siny且x∈[,时,通 常记作x= 4.做一做:(1)arcsin0= (2)aresin(-- ;arcsin 1= 答案:10(2
导航 3.填空:任意给定一个 y∈[-1,1],当 sin x=y 且 x∈ - 𝛑 𝟐 , 𝛑 𝟐 时,通 常记作 x= arcsin y . 4.做一做:(1)arcsin 0= ; (2)arcsin - 𝟏 𝟐 = ;arcsin 1= . 答案:(1)0 (2)- 𝛑 𝟔 𝛑 𝟐

导航 二、已知余弦值求角 【问题思考】 1.已知cosK之,若x∈0,,则x的值是什么?若x∈m,2ml,则x 的值是什么? 提示罕 2.填空:在区间[0,内,满足cosx-y(y∈-1,1)的x只有一个,记 作,即x=
导航 二、已知余弦值求角 【问题思考】 1.已知 ,若x∈[0,π],则x的值是什么?若x∈[π,2π],则x 的值是什么? cos x= 𝟐 𝟐 提示: 𝛑 𝟒 , 𝟕𝛑 𝟒 . 2.填空:在区间[0,π]内,满足cos x=y(y∈[-1,1])的x只有一个,记 作 arccos y ,即x= arccos y
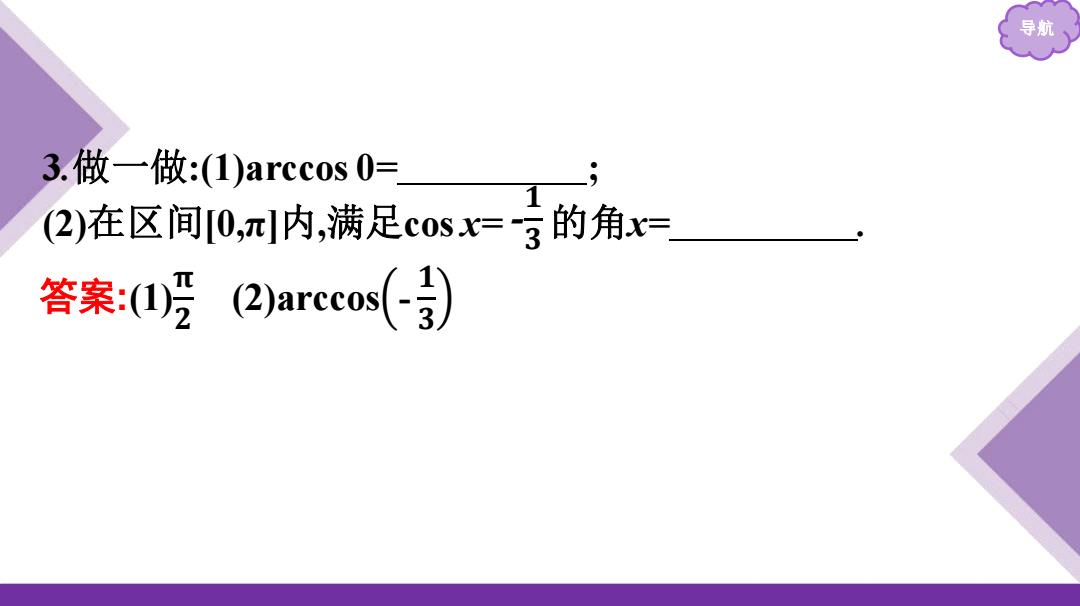
导航 3.做一做:(1)arccos0= 2)在区间0,π内,满足c0sx=3的角x= 答案:(I乃(2)Darecos(-
导航 3.做一做:(1)arccos 0= ; (2)在区间[0,π]内,满足cos x= - 的角x= . 𝟏 𝟑 答案:(1)𝛑 𝟐 (2)arccos - 𝟏 𝟑

导 三、已知正切值求角 【问题思考】 1.若x∈(,),且tanx-V3,则适合条件的角有几个?它们各 是什么? 提示:一个骨 2.填空:在区间(受,)内,满足anx与0∈R)的x只有一个,记 作,即x=
导航 三、已知正切值求角 【问题思考】 1.若 x∈ - 𝛑𝟐 , 𝛑𝟐 ,且 tan x=- 𝟑,则适合条件的角有几个?它们各 是什么 ? 提示:一个,-𝛑𝟑. 2.填空:在区间 - 𝛑𝟐 , 𝛑𝟐 内,满足 tan x=y(y ∈ R)的 x 只有一个,记 作 arctan y ,即 x=arctan y

导航 3.做一做:(1)arctan(-1)= C)arctau 3 ③若x∈(受,》,且am元,则 答案:(l)平(2%(3)arctan元
导航 3.做一做:(1)arctan(-1)= ; (2)arctan 𝟑 𝟑 = ; (3)若 x∈ - 𝛑 𝟐 , 𝛑 𝟐 ,且 tan x=π,则 x= . 答案:(1)- 𝛑 𝟒 (2)𝛑 𝟔 (3)arctan π

【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“V,错 误的画“X”. ()①arcsin表示区间(0,罗)内的一个角.( (2)若c0s-a∈[π,2,则=arccos() ③)若tan=l,则u平或( (4)在区间[0,2上,满足条件sinx=(-1≤a≤1)的x有2个.() (⑤)在区间[0,2π上,满足条件c0sx=(-1≤≤1)的x有2个.( 6)在区间-2,上,满足条件tanx-a(a∈R)的x只有1个.(
导航 【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“ ”,错 误的画“×” . (1)arcsin𝟏 𝟑 表示区间 𝟎, 𝛑 𝟐 内的一个角.( √ ) (2)若 cos α= 𝟏 𝟒 ,α∈[π,2π],则 α=arccos 𝟏 𝟒 .( × ) (3)若 tan α=1,则 α= 𝛑 𝟒 或 𝟓𝛑 𝟒 .( × ) (4)在区间[0,2π]上,满足条件 sin x=a(-1≤a≤1)的 x 有 2 个.( × ) (5)在区间[0,2π]上,满足条件 cos x=a(-1≤a≤1)的 x 有 2 个.( × ) (6)在区间 - 𝛑 𝟐 , 𝛑 𝟐 上,满足条件 tan x=a(a∈R)的 x 只有 1 个.( √ )