
全程设计 1.三角函数
1.三角函数
梳理•构建体系 归纳核心突破 高考体验
梳理•构建体系 归纳•核心突破 高 考 体 验
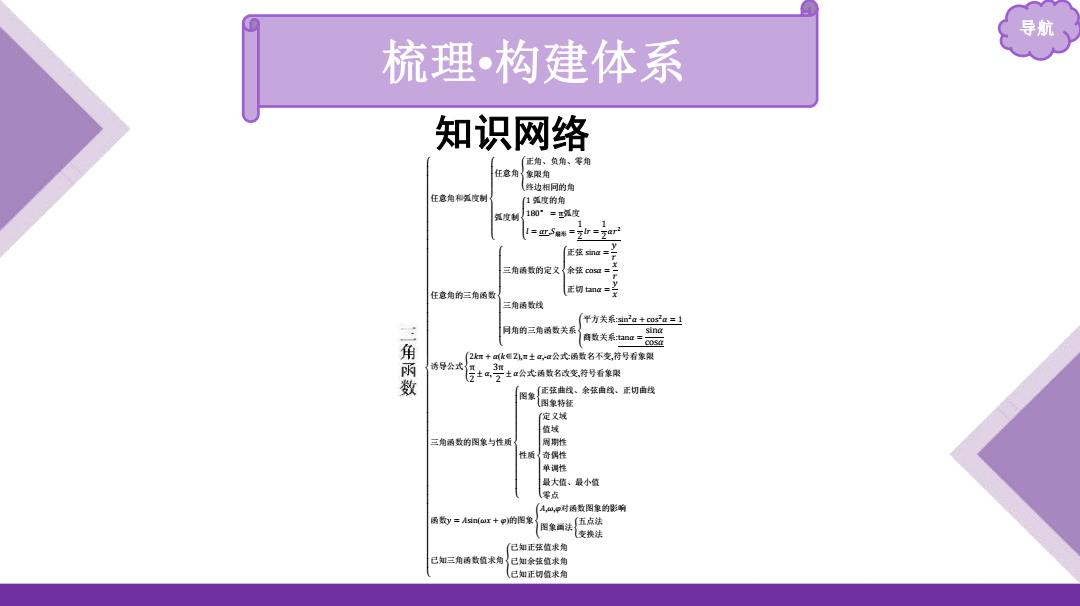
导航 梳理•构建体系 知识网络 (正角、负角、零角 任意角{象限角 终边相同的角 任意角氢度制 1度的角 度制 180”=卫填度 1 =匹5布==7 三角两数的定义 任意角的三角函数 三角函数线 平方关系如2a+cos2a=1 同角的三角函数关系 商数关系hna= sing 004 角两数 [2k红+k@Z,T士a,a公式函数名不变,符号看象限 诱导公式 土α公式两数名改变,符号看象限 图象任弦曲线、余弦鱼线。正切曲线 图象特在 定义城 值域 三角函数的图集与性质 网期性 性质 奇偶性 单调性 最大值、最小值 零点 ,仙,P对厮数图象的影响 函数y=An(ar+p)的图象 图象画法伍点法 变换法 已知正弦值求角 已知三角两数植求 已知余弦值求角 ,已知正切值求角
导航 梳理 •构建体系 知识网络 任意角和弧度制 任意角 正角、负角、零角 象限角 终边相同的角 弧度制 1 弧度的角 180° = π弧度 𝑙 = 𝛼𝑟,𝑆扇形 = 12 𝑙𝑟 = 12 𝛼𝑟2 任意角的三角函数 三角函数的定义 正弦 sin 𝛼 = 𝑦𝑟 余弦 cos 𝛼 = 𝑥𝑟 正切 tan 𝛼 = 𝑦𝑥 三角函数线 同角的三角函数关系 平方关系:si n2𝛼 + cos2𝛼 = 1 商数关系:tan 𝛼 = sin 𝛼 cos 𝛼 诱导公式 2𝑘 π + 𝛼(𝑘 ∈Z), π ± 𝛼,-𝛼公式:函数名不变,符号看象限 π2 ± 𝛼, 3π2 ± 𝛼公式:函数名改变,符号看象限 三角函数的图象与性质 图象 正弦曲线、余弦曲线、正切曲线 图象特征 性质 定义域 值域 周期性 奇偶性 单调性 最大值、最小值 零点 函数 𝑦 = 𝐴sin(𝜔 𝑥 + 𝜑)的图象 𝐴,𝜔,𝜑对函数图象的影响 图象画法 五点法 变换法 已知三角函数值求角 已知正弦值求角 已知余弦值求角 已知正切值求角
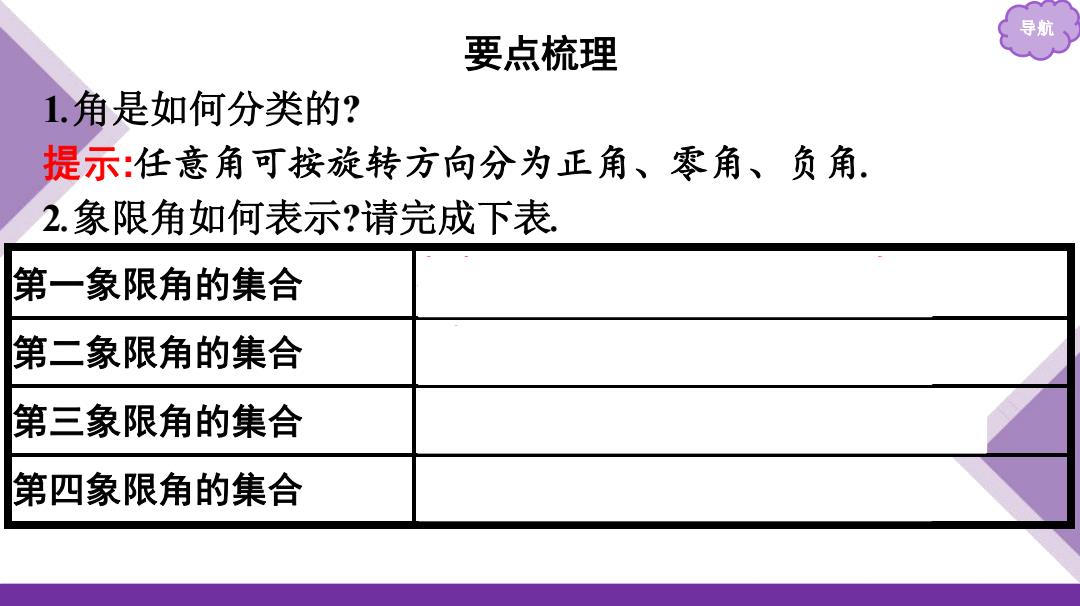
导航 要点梳理 1.角是如何分类的? 提示:任意角可按旋转方向分为正角、零角、负角. 2.象限角如何表示?请完成下表 第一象限角的集合 第二象限角的集合 第三象限角的集合 第四象限角的集合
导航 要点梳理 1.角是如何分类的? 提示:任意角可按旋转方向分为正角、零角、负角. 2.象限角如何表示?请完成下表. 第一象限角的集合 𝛂 𝟐𝐤𝝅 < 𝛂 < 𝝅 𝟐 + 𝟐𝒌𝝅,𝐤∈𝐙 第二象限角的集合 {α 𝟐𝒌𝛑+ 𝛑 𝟐 <α<2kπ+π,k∈Z} 第三象限角的集合 𝜶 𝛑+ 𝟐𝒌𝛑 < 𝜶 < 𝟑𝛑 𝟐 + 𝟐𝒌𝛑,𝒌∈𝐙 第四象限角的集合 {α 𝟐𝒌𝛑+ 𝟑𝛑 𝟐 <α<2kπ+2π,k∈Z}

导航 3.所有与角α终边相同的角,连同角α在内,如何表示? 提示:{B=2kπ+a,k∈Z☑ 4.1弧度的角是怎样定义的?度和弧度怎样转化? 提示:长度等于半径长的圆孤所对的圆心角为1弧度的角,记 作1rad.180°=πrad
导航 3.所有与角α终边相同的角,连同角α在内,如何表示? 提示:{β|β=2kπ+α,k∈Z}. 4.1弧度的角是怎样定义的?度和弧度怎样转化? 提示:长度等于半径长的圆弧所对的圆心角为1弧度的角,记 作1 rad.180° =π rad
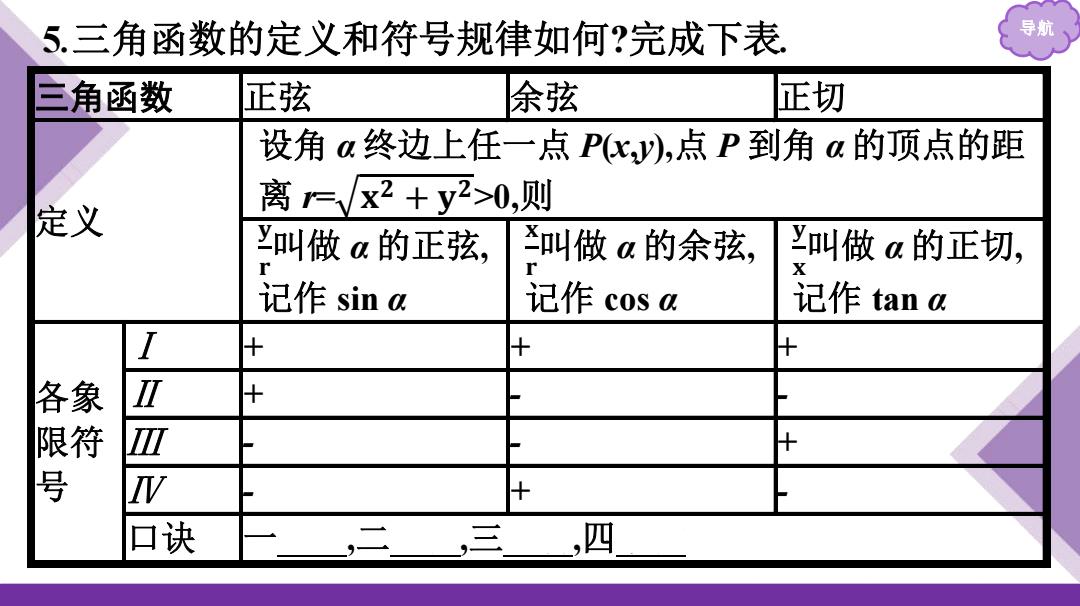
5.三角函数的定义和符号规律如何?完成下表 导航 三角函数 正弦 余弦 正切 设角a终边上任一点P,y),点P到角a的顶点的距 离=√x2+y2>0,则 定义 Y叫做a的正弦, 叫做a的余弦, y叫做a的正切, X 记作sina 记作cosa 记作tana I + + + 容 + Ⅲ 号 W + 口诀 ,二,三,四
导航 5 .三角函数的定义和符号规律如何 ?完成下表. 三角函数 正弦 余弦 正切 定义 设角 α 终边上任一点 P(x,y), 点 P 到角 α 的顶点的距 离 r= 𝐱 𝟐 + 𝐲 𝟐 >0, 则 𝐲𝐫 叫做 α 的正弦, 记作 sin α 𝐱𝐫 叫做 α 的余弦, 记作 cos α 𝐲𝐱 叫做 α 的正切, 记作 tan α 各象 限符号 Ⅰ + + + Ⅱ + - - Ⅲ - - + Ⅳ - + - 口诀 一全正,二正弦,三正切,四余弦
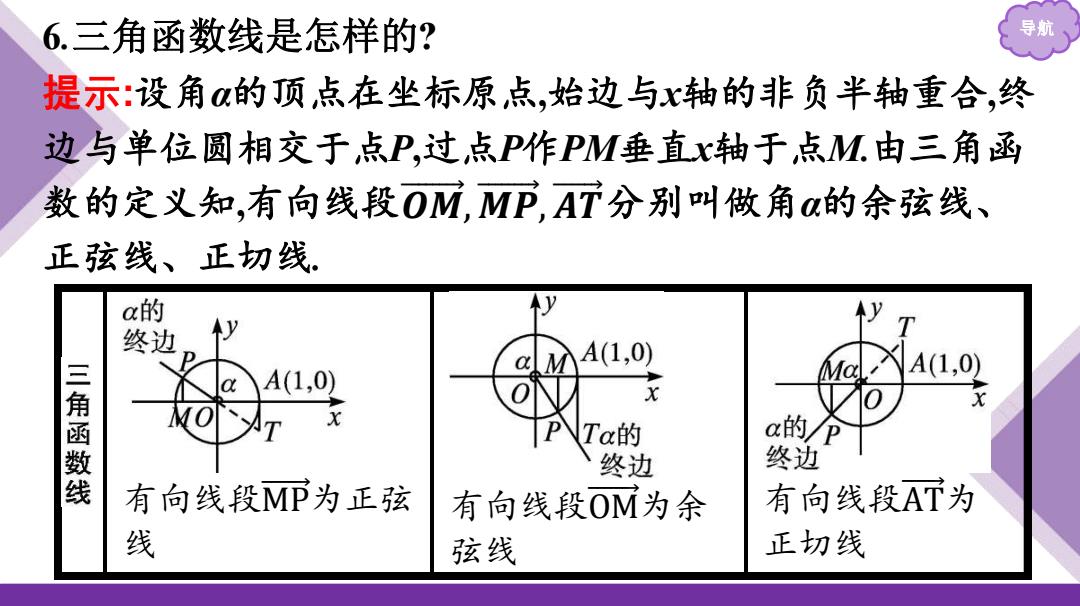
6.三角函数线是怎样的? 提示:设角的顶点在坐标原点,始边与x轴的非负半轴重合,终 边与单位圆相交于点P,过点P作PM垂直x轴于点M.由三角函 数的定义知,有向线段O☑,MP,A7分别叫做角α的余弦线、 正弦线、正切线 a的 终边 y A(1,0) 三角函数线 A(1,0) A(1,0) x D Ta的 a的/P 终边 终边 有向线段MP为正弦 有向线段OM为余 有向线段AT为 线 弦线 正切线
导航 6.三角函数线是怎样的? 提示:设角α的顶点在坐标原点,始边与x轴的非负半轴重合,终 边与单位圆相交于点P,过点P作PM垂直x轴于点M.由三角函 数的定义知,有向线段 分别叫做角α的余弦线、 正弦线、正切线. 𝑶 𝑴 , 𝑴 𝑷 , 𝑨 𝑻 有向线段MP 为正弦 线 有向线段OM 为余 弦线 有向线段AT 为 正切线

导航 7.同角三角函数的基本关系式有哪些? sing 提示:sin2a+c0s2a=1,tana= cosa
导航 7.同角三角函数的基本关系式有哪些? 提示:sin2 α+cos2 α=1,tan α= 𝐬𝐢𝐧𝜶 𝐜𝐨𝐬𝜶

导航 8.诱导公式有哪些?请完成下表 角 2kπ+a "ia 3 3 (k∈Z π+u -a 元-0 +0 -0 2 2 sin a -sin a -sin a 正弦余弦正切 cos a cos a cos a cos a cos a -cos a sin a sin a -sin a tan a -tan a 口诀 函数名,符号看象限 函数名,符号看象限
导航 8 .诱导公式有哪些 ?请完成下表. 角 2kπ + α (k∈Z) π + α -α π-α 𝛑𝟐-α 𝛑𝟐 + α 𝟑 𝛑𝟐 + α 𝟑 𝛑𝟐 -α 正弦 sin α -sin α -sin α sin α cos α cos α -cos α -cos α 余弦 cos α -cos α cos α -cos α sin α -sin α sin α -sin α 正切 tan α tan α -tan α -tan α — — — — 口诀 函数名不变,符号看象限 函数名改变,符号看象限
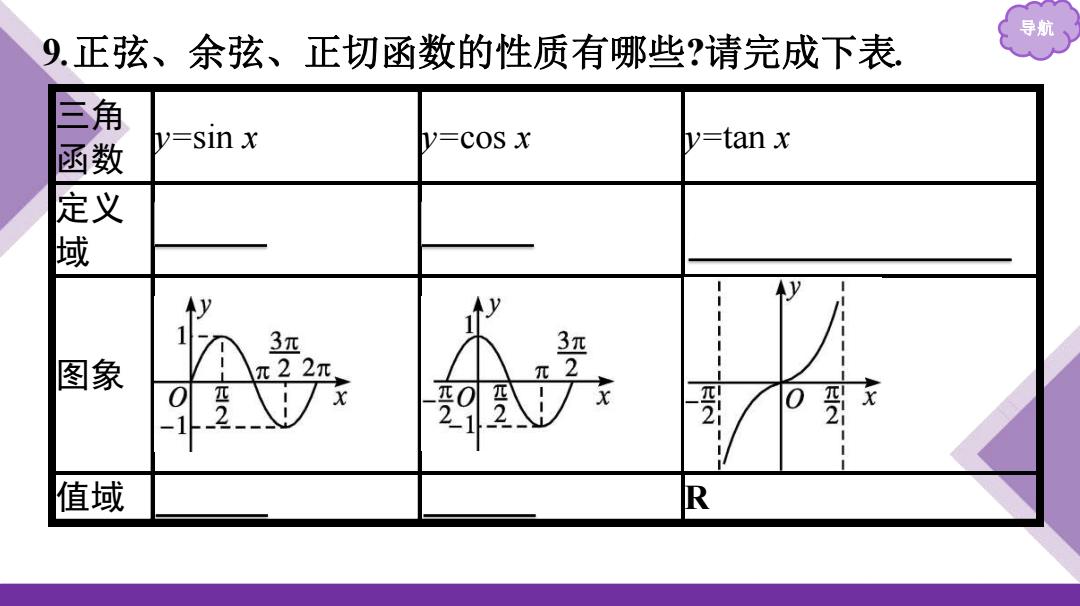
导航 9.正弦、余弦、正切函数的性质有哪些?请完成下表 数 v=sin x V-cOS x y=tan x y y y 3π 3π 图象 022平 π 匹2 0 值域 R
导航 9.正弦、余弦、正切函数的性质有哪些?请完成下表. 三角 函数 y=sin x y=cos x y=tan x 定义 域 R R {x 𝑥 ≠ 𝑘π + π 2 ,k∈Z} 图象 值域 [-1,1] [-1,1] R